Удельная энтальпия
 16 ноября, 2013
16 ноября, 2013  admin
admin Удельную энтальпию h определяют из уравнения:
|
(2.45) |
Ah - {с (7)d7.
7,
В результате интегрирования выражения для функции ср(Т) в диапазоне температур 7,-Т2 получают разницу теплосодержаний Ah материала при температуре 7, и некоторой начальной температуре (обычно принимаемой равной 0 или 20 °С).
Энтальпия необходима при расчете потребной мощности нагревательных или охлаждающих устройств, используемых при экструзии полимеров: Q = тп ■ Ah (где Q — энергия, необходимая для нагрева или охлаждения; тп — массовый расход).
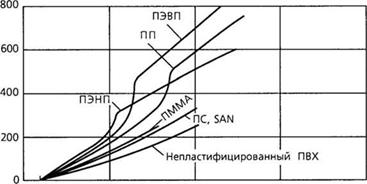
На рис. 2.30 представлены графики температурных зависимостей удельной энтальпии для различных полимеров. Дополнительные графики подобных функциональных зависимостей приведены в работе [43].
|
|
|
-с п: |
|
Ч > |
|
О 20 |
|
100 |
200 300 400
Температура Т, 'С
Рис. 2.30. Зависимости удельной энтальпии различных термопластов от температуры
у — скорость сдвига
v — скорость течения
у — направление сдвига
т — напряжение сдвига
В — динамическая сдвиговая вязкость, вязкость
г|0 — вязкость при нулевом сдвиге (ньютоновская вязкость)
ф — текучесть
тп — показатель степени в степенном законе течения (индекс течения)
к — показатель консистенции
п — показатель степени в степенном выражении для вязкости
С — характеристическая константа материала в модели Прандтля-Эйринга
А — характеристическая константа материала в модели Прандтля-Эйринга
А — характеристическая константа материала в модели Карро (соответствует нью
тоновской вязкости)
В — характеристическая константа материала в модели Карро (скорость сдвига
обратного перехода)
С — характеристическая константа материала в модели Карро (коэффициент на
клона кривой вязкости) т0 — предел текучести
Т — температура
Ph/ll — гидростатическое давление в расплаве
Т0 — опорная температура
а-г — коэффициент температурного сдвига
£0 — энергия активации течения
R — универсальная газовая постоянная
а — температурный коэффициент вязкости
Т — стандартная температура
CVC2 — а) коэффициенты уравнения Вильямса-Ланделла-Ферри б) константы в уравнении (2.40)
V — удельный объем (в PVT-диаграмме)
£ — коэффициент в уравнении (2.23)
т„, — напряжение сдвига на стенке канала
R — радиус
lg — десятичный логарифм
L — длина капилляра
Уv — скорость сдвига на стенке
V — объемный расход
Ds — эффективная скорость сдвига
s — коэффициент наклона
е — характерное среднее расстояние
ед — характерное среднее расстояние в канале круглого сечения
е0 — характерное среднее расстояние в канале прямоугольного сечения
«□ — характерное среднее расстояние в щелевом канале
rs — характерный радиус в канале круглого сечения
hs — характерная высота в прямоугольной щели
D — диаметр
рт — замеренное давление
рЕ — давление на входе в канал
eD — скорость продольной деформации
а — угол
t — время
/(г) — длина образца в момент времени t
/да — длина образца после полной усадки
— скорость продольной деформации растяжения вследствие сдвига
— начальная деформация
|
% |
— обратимая продольная деформация |
|
% |
— обратимая продольная деформация на шаге / |
|
c« |
— обратимая продольная деформация на шаге i после релаксации |
|
p |
— плотность |
|
e |
— скорость продольной деформации |
|
a |
— коэффициент линейного термического расширения |
|
X |
— теплопроводность |
|
a |
— температуропроводность (термодиффузпя) |
|
h |
— удельная энталышя |
|
Q |
— энергия, необходимая для нагрева или охлаждения |
|
m |
— массовый расход |
|
Ii |
— температура стеклования |
|
(r |
— время релаксации |
|
At, A2, |
a — коэффициенты в функциях Виноградова и Виноградова-Малкина |

 Опубликовано в
Опубликовано в