При экспериментальном определении функции течения У = /(т) или функции вязкости н =/(у, Т) в диапазоне скоростей сдвига, наблюдаемых в экструзионных головках (от 10 с-1 до 103-10[8] с-1), подходит капиллярный вискозиметр или лабо­раторный экструдер, снабженный вискозиметрической фильерой с датчиками для
измерения давления и температуры расплава. Поперечное сечение фильеры может быть круглым, кольцевым или в виде прямоугольной щели.

Принцип измерений состоит в определении в капилляре определенной геометри­ческой формы и размеров перепада давления Ар при известном объемном расходе V и при постоянной температуре расплава.

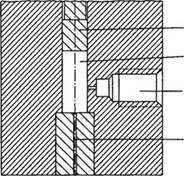
Если капилляр имеет круглое поперечное сечение, датчик давления невозможно поместить внутри капилляра вследствие его малого диаметра (в большинстве случа­ев не более 1-3 мм). Вместо этого датчик давления устанавливается в цилиндре, который имеет существенно больший диаметр. Вторая точка измерения давления относится к выходу из капилляра (рис. 2.14).

Предполагая, что течение расплава является ламинарным, стационарным, изотер­мическим, и проскальзывание на стенке капилляра вследствие прилипания отсут­ствует, напряжение сдвига на стенке круглого капилляра с радиусом R может быть выражено формулой:

Ар ■ R Ти/= 2 L ’

(2.28)

где L — длина капилляра; Ар — перепад давления.

Предполагая, что расплав полимера представляет собой ньютоновскую жидкость, скорость сдвига на стенке капилляра может быть выражена формулой:

AV *R3

yw

(2.29)

где V — объемный расход.

Примечание: уравнения (2.28) и (2.29) действительно только для круглых капилляров, однако подобные соотношения получены и для кольцевых и щелевых ка­пилляров. Более подробная информация по данному вопросу приведена в главе 3.

11а основании определения вязкости получаем:

yw

(2.30)

Рис. 2.14. Капиллярный вискозиметр: 1 — пор­шень, 2 — цилиндр, 3 — место установ­ки датчика давления, 4 — капилляр

Из уравнений (2.28)-(2.30) и известных геометрических параметров капилляра (радиус R и длина L), заданного объемного расхода И и измеренного перепада давле­ний Ар можно определить точку ( у, г|), принадлежащую кривой вязкости. Варьируя объемный расход V, а с ним и соответствующее значение скорости сдвига, можно определять вязкость в широком диапазоне скоростей сдвига.

Поправки на псевдопластичность

В предыдущем разделе предполагалось, что полимерный расплав ведет себя как ньютоновская жидкость. Поскольку такое поведение — редкость для полимерных расплавов, вязкость, получаемая описанным методом, представляет собой не истин­ную, а так называемую кажущуюся (эффективную) вязкость (например, 2).

В то время как уравнение (2.28) действительно как для ньютоновских, так и для псевдопластичных жидкостей (см. главу 3), уравнение (2.29) применимо для вычис­ления скорости сдвига только в диапазоне ньютоновского поведения жидкости. По­этому для материалов, не являющихся ньютоновскими жидкостями, рассчитывают так называемую кажущуюся (эффективную) скорость сдвига Д., которая равна ско­рости сдвига на стенке для ньютоновских жидкостей.

Для получения истинной кривой вязкости могут быть использованы два метода коррекции.

При использовании поправки Вайссенберга-Рабиновича [1,2,35] истинная ско­рость сдвига получается путем дифференцирования кажущейся кривой течения. Соотношение для истинной скорости сдвига у выглядит следующим образом:

У =Ds—T - (2.31)

3_+s 4

Здесь 5 — коэффициент наклона логарифмического графика кажущейся кривой течения:

d(lg Д)

s=— V - (2.32)

d(lgTlv)

Затем, путем деления значений сдвигового напряжения, полученных из уравне­ния (2.28), на соответствующие скорости сдвига, получают значения истинных вяз­костей. Этот метод весьма трудоемок, поскольку он требует поточечного графиче­ского дифференцирования кривой течения.

Вышеуказанный недостаток был исправлен Хмилем и Шуммером [36]. Эта по­правка была изначально описана как концепция характерной вязкости [30, 36-38]. Данный метод почти так же точен, как и предыдущий, но при этом он существенно менее трудоемок.

Основная идея поправки заключается в том, что при ламинарном, изотермиче­ском течении под давлением, которое наблюдается в канале вискозиметра или экст­рузионной головки (предполагается отсутствие проскальзывания на стенке канала и упругие эффекты пренебрежимо малы) в пределах канала всегда найдется такая
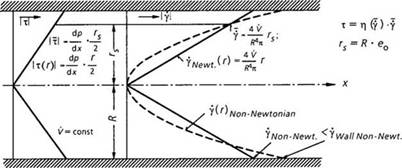
точка, в которой скорости сдвига для ньютоновских и псевдопластичных материалов совпадут (для одинаковых объемных расходов V). То есть, как только будут опреде­лены напряжение сдвига и скорость сдвига для ньютоновской жидкости, станет из­вестной и истинная вязкость для соответствующих характерных скорости сдвига и напряжения сдвига (рис. 2.15). Положение точки пересечения и, следовательно, характерный радиус канала зависят от свойств материала [38].

гs - характерный радиус капилляра у — характерная скорость сдвига т - характерное напряжение сдвига

Рис. 2.15. Определение характерной скорости сдвига для круглого капилляра

Однако для большинства полимерных расплавов характерный радиус можно при­нять постоянным. Характерное расстояние от оси круглого канала [37] представляет собой выражение:

Для канала прямоугольного сечения это выражение принимает вид:

Характерные расстояния от центра канала, полученные путем применения закона Оствальда-де Виля, были опубликованы в работе [38].

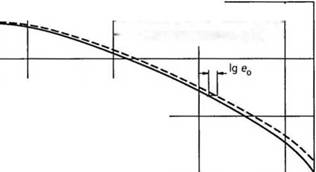
Вортбергом было показано [30], что для индексов течения т в пределах от 2 до 4 (что соответствует практике) соответствующие характерные расстояния е0 и еп могут считаться постоянными. Ошибки в результате этих допущений не превышают 1,8 и 2,5 %.

(2.33)

Далее истинная скорость сдвига может быть вычислена на основании кажущейся скорости сдвига следующим образом:

i = Dse,
где значения е могут быть получены из рис 2.16 или же расчетом по средним значени­ям величин, представленных там же.

Истинная вязкость (равная характерной вязкости) может быть вычислена с по­мощью следующего выражения:

ZW TlVе

(2.34)

которое справедливо для характерной скорости сдвига у.

Как обычно, при построении функции вязкости в виде графика с логарифмиче­ским масштабом по обеим осям, поправку получают путем сдвига по оси абсцисс на величину log е (рис. 2.17).

е0« 0,815	1 '■ tin	1 1 зЬ>т" |
— е^Г0772	hs | e<=>=Ti/2 =	F- ‘тЬг’""!	Предполага-
	^ 1 ss щ □ - щелевой канал ^ ^ о - круглый канал ^ Щ Диапазон практически Ь ^— применимых значений —^	функция течения Y = Tm

12 3 4 Индекс течения (показатель степени в степенном законе) m

0,9

S
и
о
1-
о
а»
S
I
а: о	ф
ь	лэ
и	с;
	03
Q-	I
	03
Ф	V
О
т
о.
ф
1-
*
со
CL
СО
X

0,7

0,8

Рис. 2.16. Характерное расстояние е от оси канала, представленное как функция индекса течения (показателя степени в степенном законе)

105 Па

Кажущаяся вязкость r|s (Ds)

Истинная вязкость ц (у)

10“

n(?) = ns(e0-Ds)

§ £ 9 о

103

! I

II

Учет потерь давления на входе в канал

Перепад давления, измеренный капиллярным вискозиметром, часто представля­ет собой не разницу показаний двух датчиков давления, установленных в капилля­рах, а разницу давлений, замеренных перед входом в капилляр и на выходе из него (рис. 2.14). Измеряемый таким образом перепад давления получается не только за счет трения жидкости о стенки капилляра (что является единственным корректным количественным показателем, пригодным для использования в соответствующих уравнениях для расчета вязкости), но и за счет учета так называемого перепада давле­ния на входе, который возникает в результате упругой деформации расплава на входе в капилляр. В области сужения канала частицы расплава ориентируются и вытягива­ются в направлении течения. Эта деформация переносится через капилляр в виде запасенной упругой энергии, которая на выходе из него высвобождается и проявля­ется в виде разбухания экструдата (см. раздел 2.1.3). То есть энергия упругой дефор­мации возникает, прежде всего, за счет дополнительного перепада давления. Этот перепад давления учитывается датчиком в дополнение к перепаду давления, возни­кающего в результате вязкого сдвигового течения, и поэтому должен быть исключен из окончательного результата. Сделать это можно с помощью так называемой поправ­ки Бэгли [2,39].

Поправка Бэгли [39] основана на двух основных допущениях:

1. Входной перепад давления возникает только на входе в капилляр, и, следова­тельно, не зависит от длины капилляра.

2. Давление в капилляре падает в результате течения вязкой жидкости, при этом градиент давления постоянен.

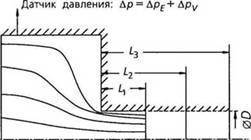
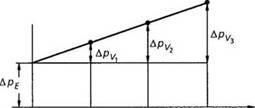
При определении перепада давления в капиллярах с различными соотношени­ями L/D (как правило, диаметр О поддерживается постоянным, а длина капилля­ра L варьируется) и при постоянной скорости сдвига получают графическую зависи­мость Др = L/D (рис. 2.18), точки которой лежат на прямой. Наклон этой прямой соответствует градиенту давления в капилляре. При варьировании скорости сдвига будет получено семейство прямых, для которых скорость сдвига является парамет­ром.

Если для этой линии выполнить экстраполяцию к нулевой длине капилляра, (L/D = 0), то пересечение линии с осью ординат покажет значение перепада давлений на входе, независимое от длины капилляра. Падение давления на входе увеличивает­ся с ростом скорости сдвига пропорционально возрастанию градиента давления в ка­пилляре.

Для получения скорректированной кривой вязкости необходимо определить раз­ницу между замеренным перепадом давления Дрт и перепадом давления на входе Аре:

АР = АРт - АРе ■ (2.35)

Именно этот перепад должен использоваться в уравнении (2.28) для определения напряжение сдвига.

Значение Др£зависит не только от скорости сдвига, но также и от типа материала: чем выше упругость расплава, тем больше будет входной перепад давления.

Др Перепад давления вследствие вязкости для развившегося потока в трубе круглого сечения:

Рис. 2.18. Принцип коррек­ции кривой тече­ния но Бэгли

др ДР^-"дТ ' 1

const

Ly/D

L2/D

L3/D L/D