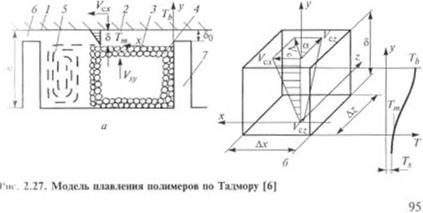
Качественная картина механизма плавления приведена на рис. 2.27, а. В соответствии с работами |23—25J, плавление матери­ала начинается при соприкосновении его с внутренней стенкой ци­линдра I. Образующаяся тонкая пленка расплава 2снимается греб­нем витка, как только толщина пленки б станет больше величины радиального зазора 6 между витком нарезки 7 и цилиндром /. Пла - стицнрованный расплав 5 собирается у толкающей кромки. Ши­рина твердой зоны по мере продвижения материала вдоль канала уменьшается, а зона расплава увеличивается, и процесс плавления заканчивается тогда, когда твердый материал 4 совершенно исче­зает.

Математическое описание зоны плавления было осуществлено Тадмором |34|. Модель строилась в предположении, что процесс плавления является стационарным, и, следовательно, поля скоро­стей и температур в каждом сечении независимы от времени. Да­лее предполагалось наличие температуры плавления твердого ма­териала в отличие от реальной температурной области плавления; считалось, что твердая зона — гомогенная непрерывная среда, а поперечные сечения канала и твердой зоны — прямоугольные. Идеализированный механизм плавления следующий: тепло к гра­нице раздела подводится через движущуюся пленку от стенки ци -

пшлра; дополнительное тепло генерируется вязкой диссипацией и пленке. Теплообменом с циркулирующим в зоне расплава поли­мером пренебрегают, так как высота твердой зоны много меньше

• ширины. Теплообменом за счет проводимости и конвекции в направлении оси винтового канала также пренебрегают. При рас - мг к* теплообмена считают, что толщина твердой зоны бесконечно нпика, поскольку коэффициент теплопроводности немонолитного таймера очень мал, и температура по мере удаления от границы l».i »дела 3быстро снижается, приближаясь к постоянной температу- |к* полимера в массе твердой юны (рис. 2.27. а). Скорость плавле­ния зависит от разности теплового потока, подводимого к границе р. цдела 3 от пленки 2, и теплового потока, отводимого от нее к I кордой зоне 4. Толщина пленки (как предсказываемая теоретичес­ки. гак и измеренная экспериментально) очень мала (около 0,02 < м) 113|, в то время как скорость движения цилиндра очень высока (около 10—110 см/с). Это обеспечивает правомерность представле­ния о движении пленки как о вынужденном потоке между двумя 1кч конечными параллельными пластинами. Верхняя пластина — пнугренняя поверхность корпуса, движущаяся со скоростью Усх и имеющая температуру Ть, а нижняя пластина — поверхность разде-

i. i фаз 3, температура которой равна температуре плавления Tg (эта iioitcpxiiocTb движется вдоль по каналу с постоянной скоростью Vxz. I'латав считается ньютоновской жидкостью.

В такой постановке уравнение теплопроводности для твердой юны принимает следующий вид:

д2Т Ку 07'

-т = —Т-. (2.13)

ду2 а5 ду 9

• I'- Г„ - средняя скорость твердого вещества в направлении у (см. рис. 2.27); о,-

• •• • |>фиииент температуропроводности твердого вещества.

Граничные условия:

у= О, Т = Tg; у = И, Г-Г0,

где Т0 — температура основном массы пробки 4, равная температуре полимера на входе в канал.

Решение уравнения (2.13) описывает стационарное распреде­ление температур в твердой пробке, движущейся с постоянной скоростью Усх (рис. 2.27, б):

Т-Tq УцУ

vr'4’— <2|4>

Уравнение энергии для расплава имеет вид:

Г

Km—T+Avf^0't (2.15)

ду

ц=т/у; (2.16)

при

у= О, Т = Tg, у =6, Г = Ть

р = const (не зависит от температуры).

Решение (2.15):

T-Ts ц(ли'с) у, у у

I'-I+f (2.17)

r„-Tg 2Km(rb-rs) &{ Sj 8

где 6 — толщина слоя расплава, зависящая от продольной координаты г; Т, у - напряжение и скорость сдвига; ДИС — модуль разности вектор;! относительной скорости корпуса и вектора скорости движения пробки:

д(? =PC-PS; лИс=[(Исг-Кк)2 + Кс2 (2 )8)

Тепловой поток от слоя расплава к поверхности раздела опре­деляется соотношением:

<2|9>

где К„ — коэф(|)нииент теплопроводности расплава.

Тепловой поток ог поверхности раздела 3 к внутренним облас­тям пробки 4 равен:

(2.20)

Разность между количеством тепла подводимым к поверх­ности раздела 3, и количеством тепла отводимым от нес втвер-

Ivк» пробку 4, — это тепло расходуемое на плавление на едини-

цс поверхности раздела материала:

8s = 8jy ~8sy - (2.21)

Вводя выражения (2.19) и (2.20) в уравнение (2.21), получим:

=х(Г» -7>)+5i^-P-c/»(7i-тоК- <2-22>

' " — удельная теплоемкость пробки полимера; Л, — скрытая теплота плавле­

нии. м — эффективная вязкость при градиенте скорости у.

Уравнение теплового баланса (2.22) связывает толщину слоя расплава 5 со скоростью движения пробки Viy в направлении оси у. Рассмотрим участок твердой зоны единичной длины (в на­правлении z)- Для этого участка количество материала, проходя­щею через поверхность раздела фаз со стороны твердой пробки, юлжно быть равно массовому расходу в пленке, причем оба эти расхода должны быть равны со — скорости плавления на единич­ной длине канала:

(2.23)

ш=^Лр,=0,5(^5рт),

in V — ширина пробки в направлении х р„ и р, — плотность расплава и твердого м. иериала соответственно.

)то уравнение материального баланса устанавливает зависи­мость между толщиной слоя расплава 6, скоростью движения пробки Vgy в направлении оси у и шириной пробки X. Уравнения (2.22) и (2.23) позволяют получить значения 5 и со как функции X, физических характеристик полимера и режима переработки:

5 = ,

(2.24) (2.25) (2.26)

I до

^СхРл

ф=.

КхР mCps(Tg-T0) + (0=Ф yfx,

K*(Tb-Tg)+№№Vcf

2[0,(7^-7о)+х]

Как видно из уравнений (2.24) и (2.25), значения 6 и со макси­ма 1ьны в начале зоны плавления, когда X — Wy и убывают до нуля при X = 0.

Для определения ширины твердой зоны было составлено диф­ференциальное уравнение материального баланса:

Xhp5 VczI. - Xhps Vcz|2+dj = oxl?, (2.27)

глс h — глубина винтового канат, которую считают равной толшине пробки.

При

где Л — высота твердой пробки, равная разности глубины винтового канала и толщины пленки расплава: А0 — высота винтового канала в начале зоны плавле­ния; р — приращение высоты канала на единице его длины (конусность).

получим решения для конического шнека в зоне плавления. Преобразуя (2.27), получим:

d, v, w

Tz(Xh) = ~i^- <228>

КмРл

Решение этого уравнения в окончательном виде после подста­новок и преобразований имеет вид:

2

Х_ 0)

W_ 0)

// х

'Л

(2.29)

1-—(2-— . 4 н)н.

// X

Фо>

//=•

(2.30)

где G - массовый расход;

(2.31)

G = V-m Pj;

- необходимая длина зоны плавления; х — тангенс половины угла конусности сердечника шнека.

Таким образом, уравнения, полученные Гадмором, показыва­ют изменения толщины пленки расплава, ширины твердой зоны, а также скорости плавления в направлении транспортировки ма­териала.