Условие равновесия для объемного напряженного состояния. Деформированное состояние твердого тела в напряженном состоянии
 10 июня, 2013
10 июня, 2013  admin
admin Тело, подвергающееся действию сил, находится в напряженном достоянии. Внешние силы, действующие на тело, бывают двух основных видов: поверхностные и объемные.
К поверхностным силам относят силы, приложенные к поверхности тела. Они могут быть сосредоточенными и распределенными. К объемным силам относят силы, действующие на все материальные точки тела и пропорциональные их массам, например силы тяжести, силы инерции.
Под действием внешних сил в теле возникают внутренние усилия.
Предел отношения внутреннего усилия Ар, действующего на какую-либо элементарную площадку, выделенную в рассматриваемой точке тела, к ее площади AF при неограниченном уменьшении последней называется напряжением ст:
![]()
Каждая тонка в напряженном теле находится под действием всех ее окружающих точек, поэтому в любой плоскости, проведенной через данную точку, будут действовать напряжение, определенной величины и направления. Полное напряжение по правилу параллелепипеда всегда можно разложить на три: одно нормальное и два касательных.
В равной мере полное напряжение можно разложить на три составляющие по направлениям осей координат.
Выделим из деформируемого тела элементарный параллелепипед с бесконечно малыми ребрами. Его плоскости проведем параллельно осям координат х, у, z. Ребра соответственно обозначим: dx dy и dz.
Полное напряжение, действующее в точке представленной в виде параллепипеда можно разложить на три нормальных напряжений.
Нормальные обозначим соответственно по осям:
![]()
Для обозначения касательных напряжений примем индекс из двух букв. Первая буква будет указывать ту координатную ось, по направлению которой
Шестью касательными.
Однако, если рассмотреть статическое равновесие элементарного
Параллелепипеда, то можно показать, что
![]()
На самом деле момент относительно, например, оси у должен быть равен нулю.
![]()
![]()
Приравнивая нулю получаем:
![]()
Аналогично составляя уравнения равновесия относительно осей х и z
Можно получить:
![]()
Отсюда следует, что напряженное состояние в точке полностью описывается шестью независимыми компонентами напряжений: тремя
Нормальными
![]()
И тремя касательными
![]()
Величины напряжений в теле, нагруженном силами и находящемся в равновесии, в общем случае непрерывно изменяются от точки к точке, т. е. напряжения являются непрерывными функциями координат. Тогда напряжения действующие на противоположных гранях элементарного параллелепипеда будут отличаться на некоторую величину, определяемую частным дифференциалом т. е. приращение какого-либо напряжения равно частному дифференциалу по той координате, по которой действуют эти
Напряжения Частный дифференциал, как известно из высшей математики, равен, для напряжений:
![]()
![]()
Для касательных напряжений:
![]()
Усилия, действующие по граням параллелепипеда, равны напряжениям, умноженным на площади соответствующих граней.
Составим уравнение равновесия, т. е. возьмем суммы проекций всех сил на оси координат и приравняем эту сумму нулю.
На ось х:
![]()
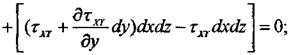
![]()
Аналогично получаем по оси у и z:
![]()
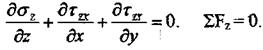
Таким образом, мы получили условия равновесия для общего случая - объёмного напряженного состояния в виде дифференциальных уравнений в частных производных.
Эти условия обязательны для всех точек деформируемого тела. Следует сказать, что три дифференциальных уравнения равновесия содержат шесть неизвестных, следовательно для их решения необходимо
Наличие дополнительных уравнений. Другими словами, объемная задача является статически неопределимой.
Теперь рассмотрим деформированное состояние тела в напряженном
Состоянии.
Если тело деформируется, то каждая точка смещается от своего первоначального положения.
Пусть координаты точки в начальный момент х, у, z, а в данный момент х', у', z' тогда:
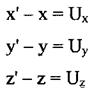
Здесь Ux? Uy, Uz представляют собой проекции перемещения на координатные оси, т. е. являются компонентами перемещений.
Для разливных точек тела компоненты перемещений различны, и они, и их производные являются непрерывными функциями координат. Другими словами тело сплошное до деформации остается сплошным после деформации.
Элементарный прямоугольный параллепипед, мысленно выделенной в теле, при деформации изменяет не только свое положение, но и свою форму. В общем случае ребра параллелепипеда изменяют длину, а углы перестают быть прямыми. Как известно, изменение длины произвольного ребра характеризуется линейной деформацией, а изменение первоначального угла между двумя ребрами характеризуется угловыми деформациями.
Рассмотрим каким образом деформации выражаются через перемещения. Для этого выделим в какой-либо точке М деформируемого тела элементарный параллепипед с бесконечно малыми ребрами dxs dy, dz, параллельными осями координат, так чтобы одна из вершин его совпадала с точкой М.
Пусть прямоугольник dbcd - проекция этого элементарного параллепипеда на плоскость ХУ до деформация, причем точка является проекцией точки М.
После деформации точки а, Ъ, с, d получают перемещения. Точка занимает положение а', в-в', c-cd-df. Выразим перемещение точек вис через перемещение точки а, Точка а получила перемещение по направлению оси X - Ux, по Y - Uy, которые являются функциями координат точки М, т. е. Ux = f(x, y,z), Uy =f(x5y? z). Точка в расположена на бесконечно малом расстоянии dx от а в направлении оси X. Поэтому перемещение точки в по X равно сумме перемещения точки а и приращению перемещений.
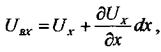
Линейная деформация ребра ав будет равна:
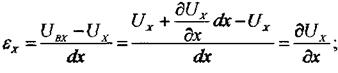
Аналогично можно получить:

Рассмотрим как определение угловые деформации через перемещения:
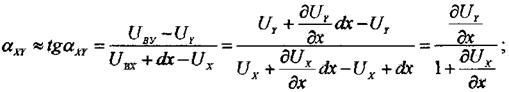
Т. к.
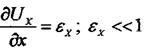
, таким образом
![]()
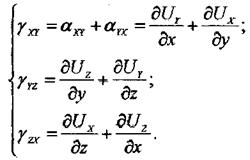
 Опубликовано в Обратотка металлов давлением
Опубликовано в Обратотка металлов давлением Комментарии закрыты.
