В основу анализа положим два предположения: 1) аксиальное напряжение не зависит от координаты 2) Материал в процессе изгиба не упрочняется.

Выделим в растянутой зоне (рис.9.3) элемент ограниченный углом , радиусом , толщиной и длиной в аксиальном направлении равной 1 и рассмотрим условие его равновесия.

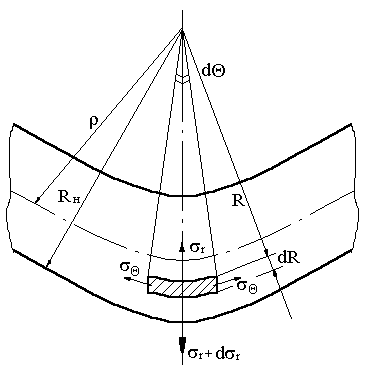
Рис. 9.3 Схема к определению напряжений в растянутой зоне.

Положим, что напряжение является растягивающим, т. е. имеет положительный знак. Уравнение равновесия элемента, при проектировании всех сил на направление радиуса будет:

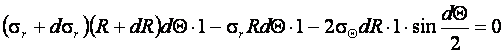(9.1)

Принимая, ввиду малости угла 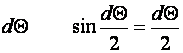, получим:

(9.2)

Или после упрощения, пренебрегая величинами второго порядка:

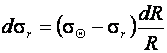(9.3)

Используя уравнение пластичности

(9.4)

Где коэффициент Лоде для плоско – деформированного состояния, равный 1,15, и решая его совместно с уравнением (9.3), получим:

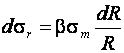(9.5)

Или после интегрирования

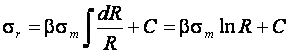(9.6)

Для определения постоянной интегрирования, используем граничные условия: при , . Тогда:

(9.7)

Подставляя (9.7) в (9.5), имеем:

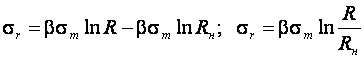(9.8)

Поскольку при любых значениях величина отрицательная, то также является величиной отрицательной, т. е. напряжение сжимающее.

Из уравнения (9.4) определим величину

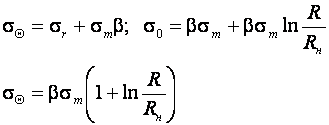(9.10)

Для определения напряжений в сжатой зоне (рис.9.4) рассмотрим условие равновесия, выделенного в ней элемента. Принимая как растягивающее напряжение, запишем:

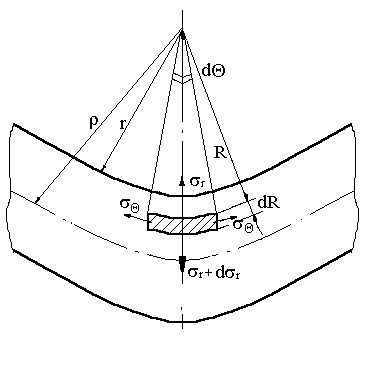
Рис. 9.4 Схема к определению напряжений в сжатой зоне.

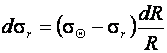(9.11)

Т. е. в общем виде для сжатой и растянутой зоны уравнения равновесия одинаковы.

Уравнения пластичности для сжатой зоны

(9.12)

Совместное решение (9.11) и (9.12) дает:

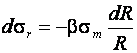(9.13)

После интегрирования

(9.14)

Исходя из условия, что при , найдем величину

(9.15)

Подставляя (9.17) в (9.16) получим

(9.16)

Так как при любых значениях величина отрицательна, то и всегда отрицательно, т. е. сжимающее. Тангенциальное напряжение будет:

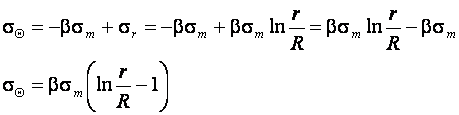(9.17)

9.3. Положение нейтрального слоя.

Определение положения нейтрального слоя и его кривизны играет большую роль при разработке технологии гибки, так как этим решаются многие вопросы и в частности: 1) определение длины заготовки, 2) определение наименьшего радиуса гибки.

Приравнивая и можно получить положение нейтрального слоя.

При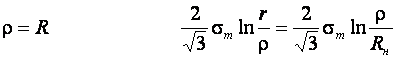

- Ренне (9.18)

Так как среднее геометрическое из 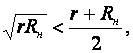то, очевидно, что нейтральный слой смещается в сторону сжатых волокон. Экспериментальные и теоретические исследования показывают, что 1) положение нейтрального слоя не зависит от механических качеств и состояния металла (упрочнен или отожжен); 2) положение нейтрального слоя определяется в основном относительной величиной радиуса гиба, т. е. ; 3) положение нейтрального слоя зависит от коэффициента утонения металла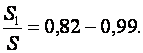

Положение нейтрального слоя можно определить по формуле Романовского В. П.

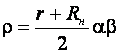(9.19)

Где коэффициент утонения заготовки –

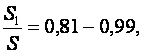
коэффициент уширения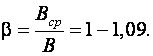

9.4. Определение минимального допустимого радиуса гиба.

Определение минимального радиуса гиба должно вестись из условия, чтобы напряжения в крайних волокнах растянутой зоны не превышало предела прочности материала.

При выводе величины радиуса положим, что нейтральный слой проходит по середине заготовки, т. е. 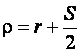, радиус гиба должен быть не равен радиусу пуансона, при подчеканке равенство этих радиусов обязательно. Для нормальных условий гибки надо не доводить напряжения гибки больше 50% от . Очевидно, что и минимальный радиус гибки должен устанавливаться по предельной деформации крайних растянутых волокон. В качестве характеристики предельно допустимой деформации лучше всего принимать величину относительного сужения , образующегося при растяжении. На рис. 8.5 длина нейтральной линии, длина растянутых крайних волокон. До гибки . Абсолютное удлинение волокна:

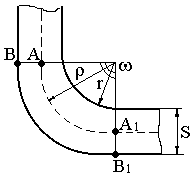
Рис.9.5 Схема к определению оптимального радиуса гиба.

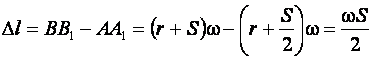(9.20)

Относительно удлинения крайних волокон:

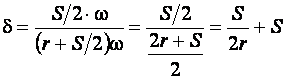(9.21)

Отсюда

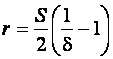(9.22)

(9.23)

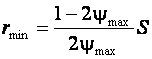(9.24)

В частности, при гибке железа , Этот вывод и полученное значение справедливо для случая гибки в направлении направлению волокон в заготовке. Если направление гибки совпадает с направлением волокон, надо принимать Значения и приведены в табл. 9.1.

Таблица 9.1.

62 55 50 45 40	0 0,1 0,2 0,3 0,43	30 20 10 4,5	0,85 1,7 4 10

Если линия гиба направлена под углом к направлению волокон, то находится между конечными значениями и .

1) если на заготовке есть заусенцы и она обращена заусенцами к матрице – радиус гиба увеличивается,

2) если эти заусенцы обращены к пуансону, то их влияние почти
отсутствует.