Напряжение является мерой внутренних сил, возникающих в теле под влиянием внешних воздействий (нагрузок, изменения температуры и др.). Для изучения напряжений в произвольной точке тела А в окрестности этой точки мысленно проводят сечение и отбрасывают одну из половин тела. Действие отброшенной половины на другую заменяют внутренними силами.

Так, например, на элементарную поверхность площадью DS (рис. 3.3) действует внутренняя поверхностная сила TN DS. При этом величину TN называют напряжением. Напряжение TN зависит только от положения точки А и направления нормали N, то есть каждому направлению n соответствует свое напряжение TN .

Соответствие напряжений TN любому направлению N устанавливается на основе принципа равновесия с помощью тензора напряжений: SIj (I = 1, 2. 3; J = 1, 2, 3,

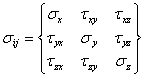. (3.11)

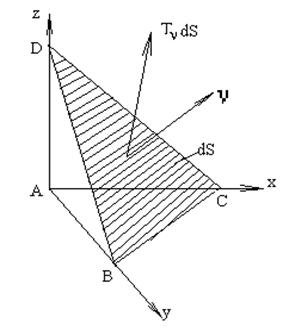
Рис. 3.3. Схема к определению поверхностных сил

И напряжений

Компоненты sx, sy, sz характеризуют нормальные напряжения на площадках, перпендикулярных осям X, Y, Z, а все остальные компоненты – касательные напряжения (рис. 3.4).

Из условий равновесия элементарного параллелепипеда с длинами ребер dx, dy, dz (рис. 3.4) (а именно из условий равенства нулю моментов сил относительно осей X, Y, Z ) следует, что

(3.12)

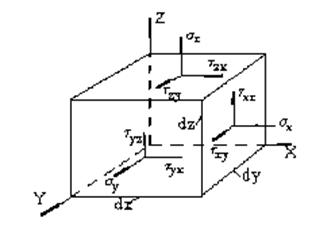
Рис. 3.4. Схема напряжений на площадках, перпендикулярных осям X, Y, Z

Таким образом, напряженное состояние в точке может быть полностью охарактеризовано всего шестью компонентами.

Так же, как и для тензора деформаций, компоненты тензора напряжений преобразуются при повороте системы координат с помощью соотношений, линейных относительно направляющих косинусов. По аналогии с деформированным состоянием имеется такое положение системы координат, при котором вдоль одной из осей нормальное напряжение максимально, а вдоль другой – минимально, причем касательные напряжения на площадках, перпендикулярных этим осям, равны нулю. Эти направления называют главными.

Главными называют и напряжения вдоль главных направлений: s1, s2, s3; s1 всегда обозначает наибольшее нормальное напряжение, а s3 – наименьшее.

Наибольшее касательное напряжение лежит в плоскости, нормаль к которой делит угол между минимальным и максимальным нормальными напряжениями пополам, и равно

. (3.13)

Три инварианта I1, I2, I3 определяют главные направления тензора напряжений и сами находятся из условия равенства нулю касательных напряжений при повороте системы координат [19].

Сумму нормальных напряжений называют Первым инвариантом I1 тензора напряжений

(3.14)

Среднее значение трех нормальных напряжений называют Гидростатическим давлением

. (3.15)

Гидростатическому давлению соответствует тензор напряжений, нормальные компоненты которого равны S0, а касательные равны нулю. Поскольку гидростатическое давление не вызывает в металле пластических деформаций, его исключают из системы напряжений. Оставшуюся часть тензора называют девиатором напряжений SS ,(I = 1, 2, 3)

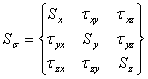, (3.16)

Где .

Кроме I1 существует еще два инварианта (I2 и I3). Второй инвариант Определяется следующим выражением [19]

(3.17)

Величины, пропорциональные корню квадратному из второго инварианта девиатора напряжений, называют интенсивностью касательных напряжений TI и интенсивностью нормальных напряжений SI:

, (3.18)