Деформациями называют изменения формы или размеров тела (или части тела) под действием внешних сил, а также при нагревании или охлаждении и других воздействиях, вызывающих изменение относительного положения частиц тела.

С геометрической точки зрения деформированное состояние в точке описывается тензором деформации [19]:

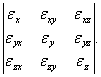(3.1)

Компоненты , характеризуют линейные деформации волокон, расположенных по осям X,Y,Z: Относительные удлинения (или относительные укорочения), А компоненты – углы поворота двух взаимно перпендикулярных до деформации волокон (или деформации сдвига).

Для компонент деформаций сдвига справедливы равенства:

, , . (3.2)

При повороте системы координат все компоненты тензора деформации преобразуются по определенным линейным относительно направляющих косинусов соотношениям. В теории деформации и линейных преобразований доказывается, что из всех возможных направлений осей координат существует тройка взаимно перпендикулярных направлений (главных направлений), относительно которых все сдвиговые компоненты деформации равны нулю. Главные направления деформаций определяются тремя скалярными величинами, не зависящими от положения системы координат и поэтому называемыми инвариантами.

Первый инвариант используется для записи условия постоянства объема деформируемого металла:

=0.      (3.3)

Второй инвариант тензора деформации имеет вид

I2= .

Величина, пропорциональная корню квадратному из второго инварианта, называется интенсивностью деформаций и используется для характеристики деформаций в общем случае деформированного состояния.

. (3.4)

В случае, когда компоненты деформаций малы по сравнению с единицей, а углы поворота малы настолько, что квадратами и произведениями их по сравнению с компонентами деформации можно пренебречь, компоненты деформации связаны с компонентами перемещений линейными зависимостями (формулами Коши). В индексных обозначениях формулы Коши могут быть записаны в виде

(гдеI,J=1,2,3,X1=X, x2=Y, x3=Z (3.5)

Или в обычных обозначениях:

(3.6)

Простейшие схемы деформирования – растяжение, сжатие, сдвиг, кручение, изгиб. Первые две схемы (растяжение и сжатие) могут быть описаны только линейными компонентами, вторые (сдвиг, кручение) – только сдвиговыми (угловыми).

В частности, при растяжении цилиндрического образца линейная деформация по оси Z определится по формуле

. (3.7)

С учетом условия (3.3) сохранения объема при пластической деформации и в силу осевой симметрии цилиндрического образца:

. (3.8)

Истинные (конечные) деформации при растяжении определятся интегрированием:

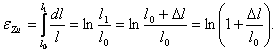(3.9)

Для сжатия знак «плюс» в формуле (3.9) необходимо поменять на «минус».

Скорости деформаций характеризуются тензором скоростей деформаций, компоненты которого определяются дифференцированием компонент тензора деформаций по времени. При этом формулы Коши примут вид

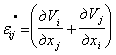, (i = 1,2,3; j = 1,2,3).   (3.10)

В тех случаях, когда заданы не сами перемещения, а скорости перемещений целесообразно определять сначала скорости деформации, а затем путем их интегрирования – деформации.

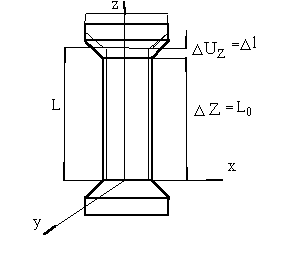
Рис. 3.2. Схема растяжения цилиндрического образца