Properties for Modeling
 21 июля, 2014
21 июля, 2014  admin
admin Accurate modeling of the development of residual stresses and strains in welded steels requires realistic modeling of the microstructural evolution. It is possible to obtain accuracy comparable to experimental measurements.
In the equations of continuum mechanics, the parameters such as thermal conductivity, elasticity tensor, the internal variables controlling plasticity or visco-plasticity are sensitive functions of microstructure. Volumetric strain rates due to phase changes and thermal expansion are the dominate loads in the stress analysis of welds. Although latent heats of solid-solid transformations do not have a large affect, they can be detected. If the weld pool shape is not taken as data, the evolution of the latent heat of fusion has a large affect in the energy equation. Solidification kinetics strongly influences the weld pool shape. Certainly, the equations for Magneto-hydro-dynamics (MHD) in the arc and the Navier-Stokes in the weld pool are much more difficult to solve than the continuum mechanics of the solid.
FEM thermal stress analyses of welds began with Ueda in 1972. In the 1980s this capability was extended significantly. With few exceptions, these analyses were Lagrangian, i. e., the FEM mesh was tied to the material. In continuum mechanics, there are two basic descriptions, resulting in two basic formulations, the Lagrangian formulation and the Eulerian formulation.
The Eulerian formulation uses spatial coordinates. With the Eulerian formulation material points move through the observed domain, which is fixed in space. The Lagrangian formulation uses material coordinates so that the observed domain deforms and no material moves into or out of the domain. The Lagrangian formulation is often chosen when the constitutive parameters in the deformation process are history dependent and the deformed geometry is unknown in advance. The Eulerian formulation is preferred when the deformed geometry is known in advance and the process is history independent and at steady state.
The arbitrary Eulerian Lagrangian formulation used initially in fluid mechanics [8 and 9] and its twin in solid mechanics, the mixed Eulerian Lagrangian formulation of Haber [10], and Koh et al. [11], has the capability to solve history independent problems with evolving fields, in which there is often a moving patch with a steady state field. No history dependent variables are involved in Haber's formulation. Ghosh and Kikuchi [12] published a paper on the arbitrary Eulerian Lagrangian formulation with the history dependent variables interpolated from a pseudo-material mesh. These results added computational cost and a possible loss in accuracy due to the interpolation across elements.
In the Eulerian formulation for steady state stress analysis with history dependence, the history is often embedded in flow lines. The flow lines are formed by the method of characteristics starting from a known inlet boundary. This was done by Dawson [13] for the rolling process, in which the deformed or current boundary locations must be known.
In an arbitrary Eulerian Lagrangian (AEL) formulation, the mesh is allowed to move with the material points or with spatial points or allowed any other convenient mesh motion or velocity. In this case, the task of computing flow lines or streamlines is not fundamentally different from the Eulerian case. One simply deals with both the velocity of material points and the velocity of the mesh.
The steady state formulation proposed by Gu and Goldak up to 1995 [6, 28 and 29] applies especially to stress analysis with history dependence and with unknown deformed boundary, particularly in weld processes. The reference mesh and the arc are fixed in space and do not move. The material moves relative to the deformed mesh at the welding speed. At the same time every node in the frame moves continuously with the deformation.
In the past two decades considerable progress has been achieved in analyzing the mechanics of welds in the liquid region using the Navier-Stokes equations and in the solid region at lower temperatures using rate independent plasticity with hardening. Progress has been slow in stress analysis in the solid region near the melting point that must deal with both the rate dependent plasticity when a material point is above 0.57m and with rate independent plasticity when a material point is below 0.5Tm.
At low temperatures roughly below 0.5Tm, the strain rate is a
nonlinear function of stress rate. To accurately predict stress, residual stress and distortion in welded structures, one must know how the material responds to a given stress or strain, i. e., which constitutive equation to use for a given state of the material and loading condition. Not only must one know which constitutive equation is most appropriate, one must know the values of material properties, i. e., the internal variables that describe this behavior such as yield stress or deformation resistance.
In this model, four interacting agents are created to solve the coupled problem. These agents are Energy, Viscosity, Material Properties and Stress. They are called in this order in each time step.
At any particular time step each finite element implements one of the three models depending on the average temperature of the element. Thus the constitutive model is element level data and all Gauss points in an element implement the same constitutive for that time step.
|
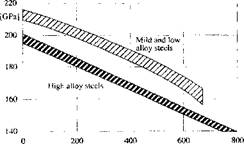
Temperature [°C| Figure 5-4: Young’s modulus for some steels, from Richter [34 andl]. |
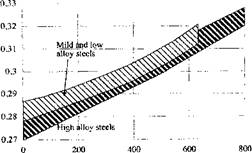
Young’s modulus and Poisson’s ratio are shown in Figures 5-4 and 5-5 for lower temperatures [34].
|
Temperature (°С] Figure 5-5: Poisson’s ratio modulus for some steels, from Richter [34 and 1]. |
The temperature in welds varies from the boiling temperature to room temperature. The domain includes the liquid weld pool and the far field of solid near room temperature. The liquid is well described as a Newtonian fluid characterized by a temperature dependent viscosity. The temperature of solid ranges from the melting temperature Tm to room temperature, where Tm is in degrees of Kelvin. At temperatures from 0.8 to 1.0Tm, the solid can be considered to be a linear viscous material characterized by a viscosity due to the diffusion of dislocations. From temperatures of
0. 5 to 0.8Tm, the solid can be considered to be viscoplastic and characterized by an elasticity tensor, viscosity and deformation resistance. Below 0.5 Tm, the solid can be considered to be a rate independent plastic material characterized by an elasticity tensor, yield strength and isotropic hardening modulus. Also three basic classes of constitutive behavior (three plastic potential functions) for low, intermediate and high temperature plasticity can be defined. All models were implemented in the same Lagrangian finite strain frame work [33]. The constitutive model was assigned to be rate independent if the temperature is less than 0.5 Tm, rate dependent if
the temperature is in a range 0.5-0.8 Tm and linear viscous if the temperature was greater than 0.8 Tm. Thus the constitutive equation of a material point had to be able to change type with space and time during the welding process. The results of the analysis in [33] agreed in a qualitative sense with the experimental results of Chihoski [47].
The rate dependent plasticity constitutive equation is only applied on the sides of the HAZ. In front of the weld pool, the temperature rise is so rapid that this mesh is too coarse to capture the thin rate dependent plastic zone. Note that the pressure is highest in this zone. Also note that the cooling weldment pulls metal back towards the weld pool. The effective plastic strain reaches a maximum some distance behind the weld pool.

 Опубликовано в
Опубликовано в