МЕТОДИЧЕСКИЕ ОСНОВЫ РАЗРАБОТКИ ЭКСПЕРИМЕНТАЛЬНО-РАСЧЕТНЫХ МЕТОДОВ
 28 мая, 2016
28 мая, 2016  Oleg Maloletnikov
Oleg Maloletnikov При сварке действует много факторов, влияющих в различной степени на конечные размеры и свойства иша и сварного соединения. К ним относятся сила тока, напряжение, скорость сварки, размеры и химический состав металла электродной проволоки или стержня, вид и состав защитной среды, размеры и химический состав основного металла, температура окружающего воздуха.
По этой причине бывает трудно оценить воздействие каждого фактора и тем более их совместное влияние, т. е. привести результаты исследования в определенную систему и установить количественные связи и соотношения.
При использовании теории подобия п анализа размерностей на основе апализа физического существа явления отыскивают совокупности факторов (комплексы), совместно влияющих на исследуемую функцию. Эти комплексы представляют собой устойчивые комбинации из факторов, существенных дли изучаемого процесса, поэтому пмеют ясный физический смысл. Заданное значение комплекса может быть получено при большом числе комбинаций из входящих в него величин, поэтому комплексы являются новыми, обобщенными переменными (параметрами) в исследуемом процессе.
В связи с тем. что определенным значениям комплекса отвечает множество совокупностей входящих в него факторов, решение задачи в этих переменных будет справедливым но только дли данного конкретного опыта, но и для бесконечного множества других опытов, объединенных некоторой общностью свойств (подобием явлений) и характеризуемых указанными комплексами. Так, например, для процесса электродуговой сварки в защитных газах функциональную зависимость между размерными физическими параметрами можно представить в виде
/ Н? U, ecu, {?з, fe, ^пл» /■» су, A", (?» ^а)~0
или на основании я-теоремы в виде уравнения с безразмерными комплексами
/і(Яі, я2, Я3, Я;)=0, (1)
где / — сила сварочного тока, A; U — напряженно дуги, кг-м2/А-С3; vCB — скорость сварки, м/с; 5пл — теплосодержание единицы объема расплавлен пого основного или электроднох'о металлов, кг/м - с2; d3 — диаметр электрода, м; b — ширина зазора под сварку, м; Я — коэффициент теплопроводности, кгм/°С • с; су — объемная теплоемкость, кг/с-м°С; S — толщина свариваемого металла, м; Q — расход газовой защитной среды, м3/с; (э — вылет электрода цри сварке, м; а = /./су — коэффициент температуропроводности, м3/с; Яц, л2, я і — безразмерные комплексы, сос. тавлеїшью из размерных величин.
Число выбранных размеров параметров п определяет число безразмерных критериев к по вираженню
к — п—т,
где га — число основных физических единиц.
В рассматриваемом случае т = 5 (кг, м, Ас, °С) и к = 11 — 5 = 6. Если принятые параметры процесса разбить на группы, которые имеют определенное физическое толкование, таї;, чтобы в каждой группе параметров п было на единицу больше, чем единиц измерений т, можно записать:
((/)>; (/)*; {vCB)V-, (,by; (Snl)V; і
|
|
Вообще же их комбинации могут быть самыми разнообразными. Поскольку размерность безразмерной величины выражается единицей, то комбинация физнчесшіх величин в группах (2) — (4) будет безразмерной,
Vi «і, Х2, Уі, у2 ЯВЛЯЮТСЯ КОріШМИ СООТЕСТСТВуЮЩИХ
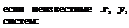
![]()
![]() 1 +Y = 0; 2+y+z — v=0; —1+»=0; — 3 — y — 2у = 0;
1 +Y = 0; 2+y+z — v=0; —1+»=0; — 3 — y — 2у = 0;
3 + a;i + I/i=0; ■> — 1 —1/1 = 0; / ^+а’г + 2у2 = 0; I
— 1 —j/2 = 0. j
После решения систем уравнений (J5) — (7) с учетом выражений (2) — (4) получаем безразмерные комплексы л;, которые можно назвать критериями подобия рассматриваемого процесса:
1и ■ _ g.
SimVcbV ’ РсвЬ* ’ а
В свою очередь, из этих соотношений можно получить п другие безразмерные критерии, так как существо их не изменяется при умножении, делении и возведении критериев в произвольную степень. Согласно уравнениям (1) и (7) функциональную зависимость процесса сварки данного вида можно записать в форме
![]() / 1 111 - g ■ Е£вМ_П
/ 1 111 - g ■ Е£вМ_П
^ил»свЬ* ’ пспб2 ’ а )
В выражение (8) с целью расширения его критерналыгости можно включить следующие симплексы: Л’, = b/d3; S2 = ljd3 S3 = бlb, включающие такие характеристики, как la, d3, 6, Ь, имеющие важное значение для описания процессов расплавления электродного металла, расхода газов и т. и. С учетом этих симплексов критериальное уравнение будет иметь вид
![]() . [ IU Q. |’<н& . Ъ 1Я _ б_0
. [ IU Q. |’<н& . Ъ 1Я _ б_0
1 1 ’ а ’ d3 ’ * Ь)
где 78 — вылет электрода, м; б — толщина изделия, м.
Функциональная зависимость или критериальное уравнение (9) характеризует в целом выбранный процесс сварки (газоэлектрическая сварка но узкому зазору), заданной параметрами уравнения (1). При увеличении числа задаваемых параметров число критериев увеличивается, поэтому вопрос о достаточности критериев в каждом конкретном случае должеи решаться отдельно.
При опытном подборе режима сварки нужно обрабатывать полученные результаты в виде зависимости между безразмерными критериями, что позволяет распространить полученные данные па все подобные явления.
Раскрывая содержание любого из критериев itj, например критерия я2 = QlvCBb2, можно критериальное уравнение (9) представить в виде
<? = 1>(;вЬ2ф(л„ л3, Slt S2, Ss),
где jt2 = rp(.4j, jt3, Sx, Ss, Sa) — неизвестная критериальная функция от всех или толі, ко от отдельных критериев и комплексов. Вид критериальной функции, как правило, определяется опытным путем, по ограниченному числі' опытов, но сама функция охватывает подобные явления для бесчисленного числа других опытов, которые можно характеризовать тем же обобщенным параметром, т. е выбранным безразмерным комплексом.
При экспериментально статистических методах исследования наиболее распространен одпофакторный эксперимент, при котором для выяспенпя влияния отдельного фактора на искомую функцию эксперимент проводят таким образом, чтобы при переходе от одного опыта к другому изменялся только этот фактор, а все остальные оставались постоянными (что трудно бывает осуществить практически). Это может внести значительные погрешности в результаты исследования и, кроме того, требует большого числа экспериментов для выявления роли каждого из факторов (при остальных факторах постоянных).
Результаты экспериментов обобщают в пиде лпнпи регрессии, вид которой определяется обычно по методу наименьших квадратов, методу подбора или другому подходящему методу. В ряде случаев результаты оформляют и впде графиков и номограмм, по которым в дальнейшем рассчитывают значения функции для искомого параметра. Общий анализ и числовая оценка явления из-за наличия большого число зависимостей, имеющих частное значение, часто оказываются весьма затруднительными.
В связи с отмеченным недостатком в последние годы все шире применяется метод планируемого многофакторного эксперимента. На основе множественного корреляционного анализа зависимость менаду искомой функцией отклика У и независимыми факторами X находится в форме полинома той или иной степени:
п п п п п п
У=к,++2 2 bijXiXj+S 2 2 bljhxixjxh+...
і г І і j h
+■••+!(10)
і m
я ри ї Ф ; фкф... ф т.
Так, например, для трехфакторного эксперимента полином будет иметь вид
У — Ь„ h3XL -|- b2X2 - J - ЬЯХ3 -[- ЬІ2Х1Х2 + Ь. гзХ2Х:і - j - bl3X1X3-j - bli3XiX2X3, (11)
где b0, bu b2... bид — коэффициенты регрессионного уравнения, определяемые но формуле
N
2 Y&i
ь І= 1
bi - jy.
где / = 0, 1, 2..., к - номер фактора (нуль записан для фактора Х„ и вычисления ft0); і — номер опыта.
Коэффициенты, учитывающие совместное влияние, определяют по формуле
N
"из — д - .
где и, / = 1, 2,..., к — номер фактора (иф/).
Адекватность полученного полинома, т. е. математической модели процесса, экспериментальным данным проверяется па основе регрессионного анализа по критерию Фишера.
Цель данного метода найти оптимум функции по минимально необходимому числу опытов. Число опытов зависит от числа независимых факторов к и числа уровней и, которые может принимать каждый фактор:
N^n*.
Наиболее часто ограничиваются двумя уровнями — верхним, условно обозначаемым величиной « +1» или просто «+», и нижним, обозначаемым
величиной « — 1» или просто « — ». 11а первом этапе работы определяют число опытов и условий их проведения, составляют матрицу планирования экспериментов, которая представляет собой все возможные комбинации сочетаний факторов, находящихся на разных уровнях.
При трех независимых факторах .гь а;2, .т3 и двух уровнях их изменения (максимальном и минимальном) наименьшее число опытов будет равно N --- 2'л - 8 и матрица планирования будет иметь вид, представленный
в табл. 39. В таблице — фиктивная переменная (для определения коэффициента Ьс), и соответствующий столбец всегда имеет знак плюс. Столбцы :rj, r2, ,т. T2.TS, учитывают эффект взаимодействия факторов, их знаки
определяются перемножением соответствующих столбцов.
|
Таблица 39. Матрица планирования
|
Для использования методов регрессионного анализа с вычислением дисперсіш желательно, чтобы для каждого номера опыта было выполнено не менее грех опытов. При большем числе опытов линия регрессии будет более точно отражать экспериментальные данные.
Для того чтобы оценить пригодность полученного уравнения, необходимо проверить ряд статистических гипотез регрессионного анализа. Приступать к регрессионному анализу можно только в том случае, если дисперсии в каждом опыте однородны. Дисперсия в каждом опыте определяется по формуле
N
™ f = і
где У(t — результат отдельного опыта; Y — среднее арифметическое всех параллельных опытов; п — 1 — число степеней свободы, равное числу параллельных опытов, минус единица.
Дисперсия всего эксперимента получается в результате усреднения дисперсий всех опытов и определяется но формуле
=-Цу----- ■»
1
где S — дисперсия в каждой строке матрицы; /, — число степеней свободы в і-м опыте; / = п — 1.
Затем проверяют гипотезу об однородности дисперсии по критерию Кохрана или Карт лета. После проверки однородности дисперсии проверяют, с какой степенью правдоподобия полученное уравнение описывает изучаемое явление; такая проверка называется проверкой адекватности получен*
ного регрессионного уравнения. Проверяют также значимость его коэффициентов. Сначала определяют дисперсию адекватности:
Л'
![]() 1_____
1_____
/
где щ — число повторных опытов в і-й строке матрицы;
АУКУі-Уі)2;
— среднее арифметическое на п параллельных опытов; — результат, предсказанный по уравнению регрессии; f — число степеней свободы;
/ = Л — (А - +1),
Л’ — число опытов; к — число коэффициентов, которые вычислены по результатам этих опытов независимо друг от друга.
В статистике адекватность (максимум правдоподобия) обычно проверяют по критерию Фишера (Г-критерию):
F — &яц/£ Y),
где, Sgд — дисперсия адекватности; S^Y) —дипсерсия эксперимента (функции отклика).
Если критерий Фишера, полученный по экспериментальным данным, меньше табличного его значения, то уравнение регрессии адекватно.
Значимость коэффициентов проверяют по критерию Стыодепта или f-критерию.
<= I bj j,
где Ibj/ — абсолютная величлпа коэффициента регрессии; 5^ j — + -) |/ (l j — квадратичная ошибка коэффициента регрессии;
Л’(Ю| =Sy)/N.
Если критерий Стьюдента, подсчитанный по экспериментальным данным, больше табличного его значения (соответствующего данному числу степеней свободы п выбранной вероятности), коэффициент уравнения будет значимым.
Наиболее целесообразно все расчеты по регрессионному анализу выполнять па ЭВМ. В этом случае значимость коэффициентов определяют в процессе расчета — по программе рассчитывают все коэффициенты уравнения регрессии, проверяют их значимость по критерию Стыодепта при вероятностях р — 0,90; 0,95; 0,98; 0,99. Переменную с минимальным уровнем значимости исключают из уравнения п расчет повторяют до исключения всех незначимых переменных.
Указанная математическая модель может служить для поиска оптимальных решений путем так называемого движения по максимальному градиенту, чтобы новые опыты проводить только в этом направлении, либо может быть использована в качестве интерполяционной модели изучаемого явления.
Полипом типа (10) позволяет выявить влияние каждого отдельного фактора и совместное их влияние. Степень влияния каждого фактора на функцию отклика легко устанавливается, если рассчитать уравнение регрессии при последовательном исключении факторов xt, .г2, ,тч. Остаточная дисперсия •?о буДет характеризовать отклонение расчетного значения функции отклика от ее экспериментального значення. Чем больше величина S£, тем большее влияние имеет исключенный из уравнения фактор.
При использовании уравнений типа (11) в качестве интерполяционной модели под величинами х2, х3 понимается отношение фактической величиям фактора к одному из предельных его значений. Это делает уравнение менее удобным для качественного анализа, который легко осуществить, если уравнение привести к натуральным параметрам:
где Хі — параметр в натуральном масштабе; Х.;о — значение этого параметра для основного уровня (нулевого); XimaxuXimin—максимальное и минимальное значения параметра в натуральном масштабе; р — интервал варьирования.
Точность статистических моделей, естественно, возрастает с увеличением числа опытов.
Ниже приведены приближенные методы расчета режимов сварки, геометрических размеров сварных швов, механических свойств металла шва из. т. в., полученные различными исследователями по экспериментальным данным при их обработке статистическими методами.

 Опубликовано в
Опубликовано в