The most popular model for the heat input is double ellipsoid, because for many arc welds the double ellipsoid shape is a good approximation. It shows that a Gaussian distribution of power density inside a double ellipsoid moving along the weld path was convenient, accurate and efficient for most realistic welds with simple shapes. Since the model reflects the depth and shapes of a weld, it has proved to be more realistic and flexible in application than previous models.

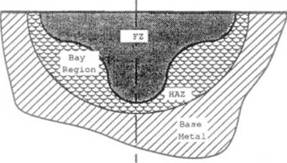
However, the power density model must generate the correct shape of the weld pool. Unfortunately, when the shape of a weld pool is more complicated than the shape of a double ellipsoid, e. g. the double pool in a submerged arc weld described by Barlow [5], Figure 3-2, it is very difficult to find a power density distribution function that accurately computes the transient temperature field.

The determination of the temperature field only by the melting point temperature at the liquid-solid interface is defined by Radaj as the equivalent heat source (equivalent, because the temperature distribution in the weld pool replaces the power density distribution). For this purpose Goldak used the term ‘prescribed temperature heat source’.

The prescribed temperature distribution function has been developed to model weld pools with more complex geometry because:

-The temperature distribution can be measured more accurately through experiment [6] than the power density distribution,

-At the liquid-solid interface the temperature can be set to the melting point of the base metal, possibly adjusted for curvature and interface speed,

-The cross-section of the prescribed volume can be measured from a metallograph as Barlow [5] and Glickstein and Friedman [7] have demonstrated,

-The effects of radiation and convection on the surface of the weld pool are already incorporated in the prescribed temperature field and need not be included in the weld model,

-The computing time is reduced because the prescribed degrees of freedom need not be evaluated.

The temperature field also can be obtained by specifying the heat input as described above or by prescribing the temperature in the weld pool. Gu et al [2] presented a model with prescribed temperature distribution in the weld pool, which demonstrates that the prescribed temperature field can model complex weld pools accurately; see section 3-4-5-1.

A finite element calculation based on an Eulerian formulation for steady state temperature fields for welds with filler metal addition derived from the transformation eq. (3-6) is also presented by Gu et al. in [14], in which the thermal diffusivity is taken as a constant, see section 3-4-5-2.