Functionality of the Data Structure
 20 июня, 2014
20 июня, 2014  admin
admin Some functionality will be required in the process to build up the flow lines. Since there are some similarities among all requirements, the required functionality will be implemented in one data structure. The data structure provides the functionality to:
1. loop over elements in the order from upstream to downstream;
2. find an element containing a given point;
3. find all points from a given set lying along a given flow line. Smalltalk has been used in the implementation of the
functionality. With the help of Object Oriented Programming, the data structure has not only been created easily, but organized nicely as well.
Layered tree description
The structure chosen can be viewed as a three-layered tree, used to hold either points on a flow line or elements. The layers do not refer to the levels of a regular binary tree. Rather, each layer consists of one or more complete trees, each one hanging off a vertex of a higher level tree. The layers represent the x-, y-, and z-axes,
|
respectively, and the ordering within a layer is with respect to the corresponding axis.
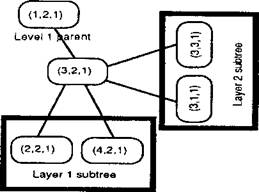
Figure 4-6: An example of the tree structure in two dimensions. The vertex (3, 2,1) is part of a layer 1 search tree based on x-coordinates, but is also the root of a layer 2 subtree based on y-coordinates. |
A concrete example with two layers is shown in Figure 4-6. On the left is the top-level tree, a binary search tree based on x - coordinates. The vertex (3,2,1) lies somewhere in the middle of this tree, with parent (1,2, 1) and children (2,2,1) and (4,2,1). However,
(3.2.1) is also the root of another tree, which is in the second layer, and whose search ordering is based on ^-coordinates. This layer 2 tree contains (in addition to the root (3,2,1)) the points (3,1,1) and
(3.3.1) . There may be many such layer 2 trees, each one independent. Furthermore, each vertex of a layer 2 tree may have a subtree in layer 3, whose search order is based on z-coordinates.
The structure may also be viewed as a tree of trees. It has the following useful property when organizing points into flow lines. Every vertex of a tree in layer 2 is the root of a layer 3 tree containing points with identical x - and у-coordinates sorted in order by a z-coordinate. This is precisely the body of a flow line in the z - direction. Similarly, by skipping the first layer, or by changing the layer ordering, we can obtain the points on a flow line in the x - direction.
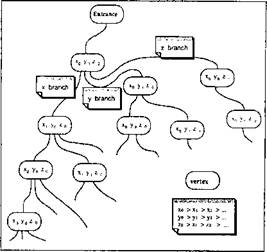
Searching a point in a binary search tree costs 0( log2 n) operations for n nodes or n equally sized elements. When element sizes vary in a mesh, a binary search tree may need an exhaustive search for an element containing a particular point. In this case, a binary tree may be less efficient than a simple sorted list. While some form of balanced binary search trees would probably provide the best performance in searching a node, quite good results in searching both nodes and elements have been achieved in the current implementation using only sorted lists. Figure 4-7 shows the current implementation of the structure in all three levels, with the different layers represented as sorted lists.
The structure in Figure 4-7 can be used to organize elements in the order that they occur along flow lines. For this purpose we make the simplifying assumption that elements can be replaced for most calculations by their axis-parallel bounding boxes. For many elements in these problems this provides a good approximation of their boundary. For the remainder, it can still reduce the number of elements for which the more expensive calculations are required, and help postpone such calculations as long as possible. This is a common technique in geometric algorithms [28].
The tree ordering in this case is based on the maximum x - y-, or z-coordinate of the bounding box, depending upon which layer of the tree is being processed. In addition, each vertex of the tree stores the maximum extent (in the appropriate direction) of any of the elements in its subtrees. This allows us to consider only the relevant subtrees in most cases. Note that if the weld source moves in a positive x-direction, the flow lines flow in the negative x-direction, the terms "maximum x" and "upstream" will be synonymous.
|
Figure 4-7: Three-layered data structure developed to store elements and to represent flow lines. When an element is stored X, Y and Z are the maximum positions of the element's bounding box. For flow lines X, Y and Z are the coordinates of the head. |

 Опубликовано в
Опубликовано в