Clipped transient temperature field
 12 июля, 2014
12 июля, 2014  admin
admin Sometimes an estimate of the steady state micro structures is desired in a temperature field computed by a transient time marching analysis. This kind of temperature field is frequently available in published data. To estimate the micro structures is to explore further the values of the old calculations. This test was performed on a mesh clipped from the example in ref. [30].
About 24 seconds after starting the weld, the weld pool and its surrounding temperature field became stable. The mesh with only the steady state temperature field was extracted, reducing the mesh size by two-thirds.
In a transient study, microstructures are computed after the transient temperature analysis from step to step. After a certain number of time steps the temperature field approaches the steady state in a finite domain near the weld pool. In this domain, however, the computed microstructures may not have necessarily reached a steady state. Before the temperature reaches steady state, the cooling rates are usually higher. The austenite grains tend to grow less. Transformation products that are sensitive to high cooling rates are more likely to form. For these reasons, a Lagrangian formulation will have to run longer to reach a steady state for microstructures than to reach a steady state for the temperature field. Because microstructures are more sensitive to the history, the steady state microstructure forms later than the steady state temperature field. This delay in the time dimension corresponds to a length in the selected spatial domain.
|
TEMPERATURE °С Min. = 20 Max. = 1800 A = 300 В = 500
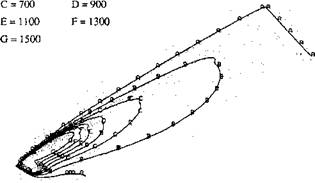
Figure 4-15: The temperature field in a weld with a complex weld pool is shown. It has been computed in ref. [30]. The mesh with these steady state contours was cut from a larger mesh in a transient time marching analysis. The microstructures in Figure 4-16 were computed for this temperature field. |
The temperature field adopted is shown in Figure 4-15. Temperature contours in this domain are stable after 62 steps in a Lagrangian calculation. An important characteristic of this temperature field is a "bay region", as described in refs [30] and [31]. In the bay area, material stays above the precipitate dissolution temperature, 1044°C for this material, for a longer period of time and cools later but possibly faster after the weld pool has passed.
|
|
|
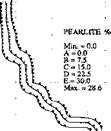
FERRITE % Min. = 0.0 Л = 10.0 В = 27.5 С -45.0 • D » 62.5 E = 80.0 Max. = 88.0 (a) |
|
|
|
(b) |
|
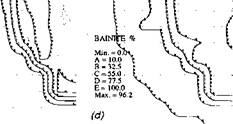
■ MARTENSITE 4 Min. * 0.0 A * 0.0 В = 1.25 С = 2,5 .. : D = 3.75 E= 5.0 : Max. = 5.24 : |
|
(e) |
|
GRAIN SIZE jun |
|
Min. = 10.0 A *50.0 • : В = 87.5 С»-125.0............. D = 163.0 E * 200.0 Max. = 216.0 |
|
|
AUSTENTIE %
Min. « 0.0 A = 0.0 В = 7.5 . С =15.0.. ...
D = 22.5 E = 30.0 :
Max. ** 100.0
(c) (f)
Figure 4-16. Microstructures at the end of flow lines. Only the interesting part at the end of the mesh (Figure 4-14) is shown. A "bay area" due to the complex weld pool shape results in an unusual microstructure. The "bay area" can be seen clearly in (c), (e), and (f), where martensite nucleates, residual austenite remains and the grain size is larger.
Figure 4-16 shows the microstructures at the downstream end, where material has experienced thermal cycles. At the end, the change of pearlite forms an outer boundary to separate the unaffected base metal from the HAZ, Figure 4-16b. There is no change to the left of contour E. To the right of contour B, a small amount of pearlite exists. In the HAZ right to the contour B, especially in the bay area, transformation products are bainite, Figure 4-16d, as well as some martensite, Figure 4-16e. The modeling of steady state microstructures here predicts that the bay is
a hard zone with the potential to initiate fractures. In the bay area, the austenite grain size, Figure 4-16f, is large, and so is the percentage of bainite and martensite. It is the only place that martensite nucleates under the current weld process conditions. Figure 4-16c shows that the decomposition of austenite has not yet reached completion in the bay area because of the truncation of the temperature field. For the existing conditions, the approximately 15% remaining austenite is likely to transform into martensite at lower temperatures.
The modeling of microstructures in a steady state weld analysis has been implemented. Relative to the Lagrangian formulations, this formulation reduces computing costs and enables higher spatial resolution to be obtained. The model also allows filler material to be added in a natural manner during welding. The test cases indicate that a reasonable accuracy could be achieved with the boundary conditions used. The model can also serve as a good predictor of a full non-linear solver. Using the current model to compute the evolution of microstructures in the steady state of a long weld reduces computing steps from hundred to one and savings in computing costs are significant. The results of the steady state analysis are also believed to be more reliable.
A data structure has been created to support this modeling. The data structure provides flow lines, which in turn provide the temperature history for every point analyzed. The data structure can also be used to find an element that determines the starting condition of a flow line. The functionality of the data structure is critical to the success of the model.
Streamlines play an important role. In a steady state temperature field described in a Eularian frame, integration along a streamline gives the thermal history of a material point. In a general FEM mesh with refinement around the weld pool, the creation of streamlines consumes more time than the microstructure calculation itself.
Since the steady state exists only in welds of simple geometry, e. g., prisms or spiral welds on pipes, the work done here focuses only on welding plates. However, the code developed can be used for prisms with any cross-sectional shape. It can also be used when the plate bends into a circular arc, as in the case of welding large
diameter pipes. The only change necessary is to use a polar coordinate system for the streamlines. Note that this change may not be applicable for thermal analysis.


 Опубликовано в
Опубликовано в