Приведенные выше экспериментальные данные и за­висимости для определения коэффициента остаточной пористости 8Г и относительной деформации сжатия 8Х со­ответствуют условию, когда при компрессии цементного геля вследствие значительной жесткости стенок формы отсутствуют поперечные деформации, т. е.

6j, = 62 = 0.

Если обозначить напряжения в цементном геле перпен­дикулярно действию приложенного нормального давле­ния РХ = Р через Ру и Pz, тогда условие объемного сжа­тия в компрессионном приборе можно выразить следую­щим образом:

Ру — Pz — %X == К>Р • Коэффициент бокового давления £д при сжатии без бо­ковых деформаций, т. е. 6^ = 82=0, выражается отноше­нием поперечных сжимающих напряжений к продоль­ным, т. е.

£Д = py/p = pt/p = pz/p. (3.29)

В отличие от нормальных (несжимаемых) жидкостей, для которых Px = Py=Pz и £д=1 (закон Паскаля), ко­эффициент бокового давления цементного геля меньше 1 и зависит от сил сцепления между частицами твердой фазы.

При сжатии цементного геля нормальной густоты под давлением Р=0,25 МПа £д=0,5—0,36 и по мере увеличения внешней нагрузки в диапазоне 2—20 МПа коэффициент £д изменяется в узких пределах: от 0,3— 0,27 до 0,26—0,25 [4]. Благодаря наличию сил сцепле­ния между частицами боковое давление распространя­ется на определенный объем цементного геля, вызывая его уплотнение.

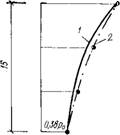
В пространстве, ограниченном жесткими стенками (при условии, что 8у=т^6х = 0), нормальное давление, приложенное к цементному гелю (испытуемого слоя) убывает по криволинейной закономерности (рис. 3.12) вследствие потери при деформации цементного геля ча­сти давления на преодоление внутреннего и поверхност­ного сопротивления (трения о стенки формы) в процес­се гидродинамической фильтрации жидкости [7].

Ро

F

Рис. 3.12. Распределение прессующего давления по высоте уплотненного цементного геля

Рассматривая цементный гель как сжимаемую жид­кость в соответствии с зако­ном Пуазейля для адиабатиче­ских явлений [95], можно оп­ределить характер распределе­ния давления в цементном ге­ле по высоте уплотняемого слоя H. Примем за начало ко­ординат точку на поверхности цементного геля, помещенного в пресс-форму, и направим ось х вниз. Допустим, что си­ла внутреннего сопротивления Г, возникающая при деформа­ции сжатия, изменяется про-

Порционально Градиенту дав - теоретическая кривая;

2 — кривая, построенная по экспериментальным данным

Tlx = — dPx/dx. (3.30)

(3.31)

Если Рх— нормальное давление на расстоянии х от мес­та приложения постоянно действующей сжимающей на­грузки, т. е. P=const, тогда сила Т может быть выраже­на соотношением:

Т = т0 (Рх/ахР),

Где ах — коэффициент потери давления, зависящий от геометриче­ских размеров пресс-формы: при квадратном основании а* =1,7; при прямоугольном — ах=2; Т0—внутреннее сопротивление в слое цементного геля, прилегающем к плоскости приложения нормального "давления.

О

Подставив Т из (3.31) в уравнение (3.30), получим

Разделим переменные и проинтегрируем (3.32) в со­ответствующих пределах:

Р

После взятия интеграла будем иметь

Ления:

(Т0/Р) nh = ax (In Р In Pji),

Поскольку Го=/г£дЛ после подстановки окончательно получим

(3.33)

Для определения степени сходимости значений Рп с экспериментальными данными, полученными при прес­совании цементного геля Х=0,876 Кя. т под давлением Р = 5 МПа в форме с квадратным основанием: fr =2,20 (см. рис. 1.11, а) £д=0,27 вычислим Ри в интервале h—5, 10, 15 и 20 см. Этим параметрам соответствует /^=0,594; ах берем равным 1,7. В таком случае фор­мула (3.33) будет иметь вид:

Ph = P/e°<35lnh

По зависимости (3.33а) получим: при H = 5 см Рн = = 3,4 МПа, при H= 10 см Ph=2,5 МПа, при H = 15 см Ph = 1,9 МПа и /2=20 см Ph= 1,55 МПа. Как видно из рис. 3.12, теоретическая кривая распределения давления по высоте образца практически совпадает с эксперимен­тальными точками и по своему виду соответствует ана­логичным закономерностям, приведенным в работах по механике грунтов [100, 125].

По вычисленным значениям Рн можно судить о том, что на глубине слоя h=20 см приложенное нормальное давление из-за значительных потерь на трение и преодо­ление внутреннего структурного сопротивления умень­шилось почти в 4 раза. Отсюда следует, что различные слои цементного геля должны отличаться по своей плот­ности и тем значительнее, чем больше удалены они от поверхности приложения внешнего нормального давле­ния, поэтому необходимо оценивать физико-механиче­ские и деформативные свойства цементного геля по средневзвешенной плотности, которая создается под дей­ствием некоторого среднего прессующего давления Рср.

(3.33а)

Отсюда

Как следует из формулы (3.28), чем больше Р0, тем больше при сравнительно малых значениях Р цемент­ный гель будет приближаться к линейно-деформируе­мым телам. В общем же случае зависимость между де­формациями и напряжением (давлением) является не­
линейной и определяется выражением: Е (ег) =dP/db. Если допустить, что цементный гель изотропен, а модуль деформации его различен по высоте испытуемого образ­ца и предопределяется пористостью или плотностью в данной точке, то при сложном напряженном состоянии можем написать:

Ddy = 1 /Е (ег) (DPy - Ir DPz - |In DPx]), (3.34)

Где Е(ег)—переменный модуль деформации, зависящий от напря­женного состояния и соответствующей характеристики цементного геля; Jin — коэффициент Пуассона, принимаемый обычно за постоян­ную величину.

Поскольку коэффициент бокового давления £д опре­деляет соотношение главных напряжений при отсутст­вии поперечных деформаций, т. е. d8y=d8z=0, а dPy — dPz—^dPx, тогда из уравнения (3.34) будем иметь

° = — — Ит1>

Откуда находим зависимость, полученную для грунтов [46]:

Ип^д/О + Сд)' (3-35)

ИЛИ

Сд = 1*п/(1-Цп)- (3.36)

Для воды £д=1, тогда |хп = 0,5. Для цементного геля коэффициент Пуассона может принимать различные значения, например: при £д=0,6 р, п=0,375; при £д=0,3 хп=0,264 и при £д= от 0,27 до 0,25 соответственно jmn= =0,212 и 0,2.

Интересно отметить, что значение in для цементного геля близко к характерным для таких твердых тел, как мрамор — |1П = 0,221; бетон—хи= от 0,2 до 0,23; гра­нит— |iri=0,196; сталь — jmn=0,28. Отсюда следует, что коэффициент Пуассона мало зависит от физического со­стояния тела: чем больше частицы твердой фазы испы­тывают сопротивление боковому смещению при сжатии (больше прочность структурных связей), тем меньшая доля приложенного давления будет передаваться в сто­роны. Если цементный гель, характеризующийся доста­точно плотной структурой, разжижить, то в этом случае р, п~0,5, т. е. соответствует вязкой жидкости. Тогда, со­гласно закону Паскаля, давление в жидкости будет по­стоянным во всех направлениях.

Если для d8z и d8x написать выражения, аналогич­ные (3.34), т. е.:

= 1/Н (ег) [dPz - iu (dPx + dPy)]; ddx = 1 /е (вр) [dPx - |In (dPy + dPz)],

И сложить их, полагая что dPv=dPz и dPx=dP, (dPy)/ J(dPx) = (dPz)/(dPx)=lД, тогда, подставив эти значения в соответствующее уравнение, получим

При изменении коэффициента пористости от некото­рого произвольного значения ег до величины er+der мо­жно в соответствии с выражением (3.27) определить приращение объемной деформации в следующем виде [125]:

DSx = — der/(l + er); Подставляя это значение d8x в (3.37), будем иметь:

Р(1+8р)

Е"= (der)«dPx) ' (3'38)

О (1-Ы0+2Сд) ,„ ад, Р - ^ • (3-39)

Занимая некоторое промежуточное положение между вязкими жидкостями и упругими телами, цементный гель при Х> 1 ведет себя как вязкопластичная система и только при Х= 1 в нем слабо проявляются упругие свойства, которые все более начинают возрастать по ме­ре отжатия из цементного геля жидкой фазы. Однако и в этом случае в значительной степени деформации но­сят остаточный характер, в связи с чем деформативность цементного геля при Х^.1 и Р^0,065 МПа обоснован­нее характеризовать модулем деформации, отличаю­щимся тем, что он соответствует полной (суммарной) деформации. Здесь уместно отметить то, что формулы теории упругости при рассмотрении деформаций сплош­ных масс могут быть применены и в том случае, если эти массы не обладают явно выраженными упругими свой­ствами. Достаточна лишь линейная зависимость между деформациями и напряжением. Это условие соблюдает­ся, так как участки АВ на компрессионных кривых для цементного геля при Х^.1 вполне можно заменить пря­мыми.

В таком случае, взяв производную от выражения (3.256), получим

Der/DPx = — 0,18 (ег0 - 0,133) Р°<18/(Р + Р,)1'18.

Подставив полученное значение dzr/dPx в (3.38), окон­чательно получим

Ег = р (1 + ег)/0,18 (8Г0 - 0,133) (Р + P0)0'18/Pg'18, (3.40)

Где коэффициент (3 определяется по формуле (3.39), а Р — соответ­ствует среднему его значению, вычисленному по формуле (3.33), т. е. Pcp=(P+Ph)/2.

Зависимость (3.40) учитывает увеличение деформа - тивных свойств цементного геля по мере повышения его плотности и структурной прочности с ростом приложен­ного нормального (прессующего) давления. В соответ­ствии с положениями работы [46], значение Ег, опреде­ляемое по формуле (3.40), можно назвать «обобщенным модулем Юнга», а величину, выраженную формулой (3.35), «обобщенным коэффициентом Пуассона».

Пользуясь формулой (3.40) и компрессионной кри­вой, приведенной на рис. 3.9 (кривая 2) для цементного геля нормальной густоты (ег=0,514 и Р0=0,065 МПа), можно вычислить значения Ег при Р, равных 0,22; 2; 10; 30 и 50 МПа (табл. 3.3.).

ТАБЛИЦА 3.3. ЗНАЧЕНИЕ Е р ПРИ РАЗЛИЧНЫХ ПРЕССУЮЩИХ ДАВЛЕНИЯХ

Р, МПа	8г		Р	1,18 (Р+Р0), МПа	0,18 Р0, МПа	£г, МПа
0,22	0,423	0,36	0,81	3,47		6,25
2	0,339	0,3	0,86	35,8		65
10	0,301	0,27	0,884	251,8	0,926	470
30	0,26	0,26	0,888	835	1560
50	0,248	0,25	0,9	1532		2909

Данные табл. 3.3 показывают, что цементный гель оптимального влагосодержания, т. е. при Х=0,876 (Р = = 0,22 МПа), характеризуется модулем Ет, соответству­ющим модулю деформации глины оптимальной влажно­сти— £=6,3 МПа [46]. По мере увеличения плотности цементного геля модуль Ет возрастает, и при ег=0,248 он достигает значения 2909 МПа, присущего, например, ряду реальных твердых тел со сформировавшейся струк­турой. Порядок чисел, характеризующих модуль £г, вполне реален и это свидетельствует о том, что формула (3.40) достаточно полно функционально связывает пара­метры, определяющие модуль Ег цементного геля.