Скорость как гомогенной, так и гетерогенной реакцли при постоян­ном давлении и неизменном количестве посторонних прямесей зависит от температуры и концентрации реагирующих веществ. Как было пока­зано в § 4-2, зависимость скорости химической реакции от концентра­ций реагирующих веществ выражается законом действующих масс.

С ростом температуры скорость химических реакций горения очень быстро возрастает. Константа скорости реакции & характеризует собой скорость химической реакции при данной температуре. Следовательно, для нахождения зависимости скорости химической реакции от темпера­туры достаточно определить температурную зависимость к.

При изучении химических реакций было замечено, что если от­кладывать 1п& как функцию обратной величины от абсолютной темпе­ратуры, то опытные данные ложатся на прямой линии.

■Поэтому была предложена зависимость константы скоро­сти от температуры в виде:

1п К=-4г + Ъ (5-5)

RT

Или в дифференциальном выражении:

D, In k Е

(5-6)

DT RT2

А в экспоненциальной форме:

Е

RT

&=^0е (5-7)

В формулах (5-5), <(5-6) и (5-7):

Е и &о — эмпирические константы;

7? = 8,321 кДж/(моль-К)—универсальная газовая постоянная;

Т — абсолютная температура.

Объяснить сильный рост скорости реакции с температурой трудно. Это нельзя объяснить увеличением числа столкновений молекул с ро­стом температуры, так как по сравнению со скоростью реакции оно возрастает очень слабо. Известно, что физические свойства по сравне­нию с константой скорости реакции изменяются с температурой слабо. Поэтому. при попытке объяснить большой температурный коэффициент скорости реакции исходили из того, что существует большой темпе­ратурный коэффициент некоторой другой величины, что и натолкнуло на мысль о том, что реагировать способны не все молекулы, а лишь молекулы, находящиеся в данный момент в особом (богатом энергией) состоянии, которые были названы «активными молекулами». Активные молекулы образуются эндотермически из нормальных молекул. Про­цесс, при котором изменяется энергия молекул без химического превра­щения, называется активацией, а теплота, поглощаемая при образовании активных молекул, называется теплотой активации. Между нормальны­ми и активными молекулами существует равновесие. Константа этого равновесия и является величиной, обладающей большим температурным коэффициентом.

Если теплота образования активных молекул равна Е, то темпера­турная зависимость константы равновесия

С акт

К акт —■

Сп ’

Где Сакт — концентрация активных молекул, а Сп — концентрация нор­мальных молекул, выражается уравнением (4-13):

D 1п К акт Е

Ш = ят* *

Далее предполагается, что концентрация активных молекул очень мала по сравнению с концентрацией нормальных молекул, поэтому кон­центрацию последних можно считать постоянной.

Тогда получим:

D In Сакт

ЙТ ЯТ2 ’

Так как константа скорости реакции к пропорциональна концентрации активных молекул, то

К__ Е

ЙТ ЯТ* ' I0'5/

Таким образом, мы получили уравнение температурной зависимости константы скорости реакции.

Согласно этому закону (Аррениуса): логарифм скорости реакции как функция от 1/Т изображается прямой линией. Угол наклона этой прямой определяет энергию активации.

Закону Аррениуса, имеющему эмпирическое происхождение, была дано два объяснения: термодинамическое и статистическое.

Для объяснения этого закона по первому способу возьмем обрати­мую реакцию

TOC o "1-5" h z А + +

Пусть &1 — константа скорости прямой реакции; — константа ско­рости обратной реакции.

Константа равновесия, определяющая состояние смеси,

К ___ ^2

"*Г ’

Подчиняется уравнению (4-13):

СИпК <2

dT ЯТ* *

Но ln/(=ln&2—ln&i; кроме того, принимая по аналогии, что

Q ~ Ez—Ei,

Получаем:

Dinkz d In &i Ег Е

DT dT RT2 RT* ‘

Последнее уравнение позволяет представить изменение константы скорости с температурой в виде

D In k____ Е

~1Г~^~ЯТГ ’

Таким образом, от уравнения температурной зависимости констан­ты равновесия мы перешли к уравнению Аррениуса. Кроме того, полу­чили, что тепловой эффект реакции равен разности между энергией активации продуктов реакции Е2 и энергией активации исходных ве­ществ Е1.

Химическая реакция может произойти после того, как будут разру­шены химические связи в молекулах исходных веществ и последние станут способными к перераспределению. Поэтому независимо от на­чальной величины энергии системы для осуществления реакции необхо­дим предварительный расход энергии на полное или частичное разло­жение молекул, соответствующий энергии активации.

Как было показано в § 5-2, химические реакции горения протекают не согласно стехиометрическим уравнениям, а через ряд промежуточных 60

Состояний с образованием активных промежуточных продуктов. Обра­зование промежуточных продуктов в виде атомов и радикалов связано - с расходом энергии. Поэтому необходимо предварительно затратить определенное количество энергии, чтобы реакция могла пройти данный этап независимо от того, как много энергии выделится при последую­щем ее протекании. Следовательно, можно представить, что протеканию реакции препятствует некоторый энергетический барьер, для преодоле­ния которого и требуется энергия активации.

Е

В

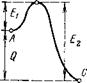
Рис. 5-1. Изменение энергии в процессе акти­вации и реагировйния.

Сказанное можно пояснить графически с по­мощью рис. 5-1. Молекулы исходных веществ, находящиеся в состоянии А, поглощая опреде­ленное количество энергии, равное энергии акти­вации Еи переходят в активное состояние В, в котором они могут реагировать, образуя про­дукты реакции с выделением энергии Е2.

Г

В большинстве случаев теплота, выделяемая на участке ВС, больше, чем поглощаемая на уча­стке АВ и разность соответствует положительно­му эффекту (2. Если же Е{>Е2, то реакция яв­ляется эндотермической.

Энергия активации представляет собой глав­ный фактор, определяющий скорость реак­ции: чем меньше энергия активации, тем быстрее протекает реакция.

При статистическом объяснении закона Аррениуса исходят из того», что для наступления реакции прежде всего необходимо столкновение реагирующих молекул. Если, например, бимолекулярная реакция про­исходила бы при каждом столкновении, то химическое превращение совершалось бы мгновенно.

Однако число столкновений молекул при данных температуре и давлении, вычисленное на основании кинетической теории, как показы­вают опыты, во много миллионов раз больше числа молекул, вступаю­щих в реакцию.

Следовательно, в реакцию вступают не все молекулы, а только - активные молекулы. Для одной и той же газовой смеси трудно предста­вить, чем могут различаться эти активные молекулы от нормальных, кроме как величиной своей энергии, а именно содержанием избыточной энергии. При столкновении этих молекул выделяется энергия в количе­стве, достаточном для разрушения химических связей, и тогда пере­группировка молекул и атомов становится возможной.

Было также замечено, что скорость реакции с ростом температуры резко увеличивается, тогда как число столкновений увеличивается при

Этом лишь в малой степени. Это может быть объ­яснено сильным ростом с температурой числа мо­лекул с повышенным энергетическим уровнем.

Имея в виду, что число молекул, энергия ко­торых превосходит некоторое заданное значение с температурой изменяется по закону, одинако­вому с законом изменения скорости реакции, можно прийти к гипотезе: для наступления реак - ции столкновение должно происходить между ^ молекулами, обладающими избытком энергии над критическим уровнем ее.

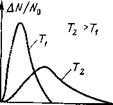
Рис. 5-2. Распределение Перейдем к обоснованию этой гипотезы. Из

Энергии в газе. закона распределения Максвелла — Больцмана,

Графически изображенного на рис. 5-2, видно, что в газе имеется неболь­шое количество молекул с очень большими, а также и очень малыми значениями скоростей. Для химической реакции представляют интерес только молекулы с очень большими скоростями, обладающие повышен­ной энергией.

TOC o "1-5" h z Число молекул, обладающих энергией, равной или больше Е, равно: Nco 00 ^ ^ Д

ЛГ= | £глг = -^|е ДГ <Ш = ЛГ,[-е ]"=ЛГ. е *Г. (5-9)

«Е Е

В формуле: с1Ы — число молекул, обладающих скоростями между V? и ХР+йУР, согласно закону распределения равное:

= е~~*Г<1Е, (5-10)

Где N0 — общее число молекул.

Подстановка выражения (5-10) в уравнение (5-9) иЛ последующее интегрирование дает:

(5-и>

Откуда видно, что доля молекул, обладающих кинетической энергией, - равной или большей, чем Е, определяется выражением е-Е1вт.

Например, в горючем газе с энергией активации Е — =83 800 МДж/моль при 7=300 К доля молекул, обладающих энерги­ей, большей, чем £=83 800 МДж/моль, равняется:

83 800

ЯГ ___ 8,321-300

-а при Г = 1000 к

Е 83 800

ЯТ _________ 8,321-1000

Следовательно, при повышении температуры от 300 до 1000 К число молекул, обладающих энергией, большей, чем 83,8 МДж/моль, увели­чивается в е~10: е~33’3 = е+23’3= 1,26-1010 раза, тогда «ак число столкнове­ний при этом увеличивается лишь в

Т,

А общая. кинетическая. энергий газа — всего лишь в 3,3 раза.

Следовательно, повышение температуры оказывает очень благопри­ятное действие на процесс активации: сильно увеличивается число молекул, обладающих большой энергией, тогда как общая энергия уве­личивается в слабой степени, т. е. происходит перераспределение энергии.

Отсюда ясно, что большой температурный коэффициент скорости реакции объясняется большим температурным коэффициентом акти­вации.

Возвращаясь к уравнению (5-7), можно его упрощенно толковать так, что &о отвечает общему числу столкновений молекул между собой 62

В единице объема за единицу времени, Е — минимальной величине энер - гии сталкивающихся молекул, обеспечивающей эффективность столкно­вения, а &— числу прореагировавших молекул. Это положение и лежит в основе гипотезы и уравнения Аррениуса.