Зависимость коэффициента теплопроводности от температуры
 4 мая, 2013
4 мая, 2013  admin
admin В расчетах, приведенных выше, предполагалось, что коэффициент теплопроводности К не зависит от температуры и остается постоянным в рассматриваемом слое стенки. Но в действительности коэффициент теплопроводности зависит от температуры и изменяется с ее изменением во многих практических случаях на 50% и более. Вообще изменение Х в зависимости от температуры будет передаваться достаточно точно, если рассматривать Л как линейную функцию температуры:
X.= а ± Ъ • (45)
Предполагая, что коэффициент теплопроводности изменяется с изменением температуры линейно по уравнению (45), получаем, что через стенку с поверхностью Р ж2, толщиной 5 м и температурами поверхностей ^ 1И ^2 проходит следующее количество тепла:
<2 = - у [а • (*, — t2) ± ~ • (*? — Ф ] ккал/час. (46)
Сравнивая уравнение (46) с уравнением (2а), можем опреде
Лить средний, или эквивалентный, коэффициент теплопроводности Хср подстановка которого в уравнение (2а) даст действительную величину теплового потока. Этот средний коэффициент теплопроводности
TOC o "1-5" h z Хср = а ± -у (^х + 4) ккал/м • час °С. (47)
Здесь а и Ь определяются уравнением (45). Количество переданного тепла с учетом непостоянства коэффициента теплопроводности составит, согласно уравнению (47), 1
Р
(2 =----- Хс • Н1 —/2) ккал/час. (48)
Средний коэффициент теплопроводности по уравнению (47) есть не что иное, как среднее арифметическое значение из коэффициентов теплопроводности, взятых при температуре t и /г-
Графическое распределение температуры при изменяющемся коэффициенте теплопроводности будет выражаться уже не прямой, а кривой линией. Распределение этой температуры строится на основании следующей формулы:
*= Г + |/ ^ + (т + ^)2°С (49)
В этом уравнении Ь — температура стенки на расстоянии в м от поверхности с температурой £>• Если в уравнении (45) действи-
|
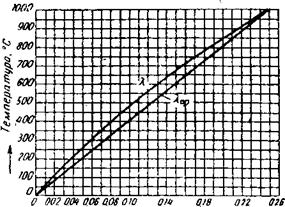
—Расстояние от холодной поверх- Мости. ju Рис. 3. Распределение температур в стенке с переменным коэффициентом теплопроводности (А,= 1+ +0,001 /). Хср = const — средний коэффициент теплопроводности |
Телен знак минус, т. е. значение Ъ будет отрицательное и X с повышением темлературы будет уменьшаться, то вместо уравнения (49) будет действительным выражение:
' = 7^ (60)
Как правило, в практических расчетах кривой распределения температуры «применяется уравнение (49), так как у большинства материалов, применяемых в технике (кроме металлов), врастет с повышением темлературы.
Чтобы дать действительную картину отклонения кривой распределения температуры от прямой линии, на рис. 3 изображена кривая распределения температуры в стенке толщиной 0,25 м с температурами поверхностей ^ = 1000° С, (2=0оС и коэффициентом теплопроводности %= 1,0 + 0,001 Л Это приблизительно соответствует теплопередаче через шамотную и динасовую стенки.
Вывод. Подставляя в уравнение (2а) значение Я, выведенное из уравнения (45), получим
<2 = (а±^-^ Аз
Или порш интегрирования
Коюстанта интегрирования определяется из граничных условий на поверхности, т. е. если 5 = 0, тогда / должна быть равна данной (самой низкой) температуре ^2* Следовательно,
<1 = г (а*2±Т '*) + с-
Принимая для другой стороны стенки граничные условия, т. е. при 5 = «о» ^ получим
Вычитая первое уравнение из второго, получим
Отсюда можно найти средний коэффициент теплопроводности, который позволит упростить довольно сложное уравнение (46). Принимая во внимание известный факт, что Л2—&2=(^1—Г^ + ^З^ можно величину и— вынести за скобки и получить из вышеприведенного уравнения следующее выражение:
= !-**)■ [а±-^-(<! + «]•
Если приравнять правую часть этого уравнения к правой части уравнения (2а), то для искомого среднего значения X получим уравнение (47). Формулу для расчета кривой распределения температуры получаем, решая квадратное уравнение для (Зя относительно I при положительном значении Ь:
,= _ — _а* 2 ((? • 5 - С)
Ь ± у Ь* + Ь Г
Вводя в это уравнение значение С, получаем уравнение (49). Так как температура'не может быть отрицательной, то корень имеет физический смысл лишь при положительных значениях данного выражения. Подкоренное выражение непосредственно показывает, что распределение температуры происходит по кривой, а не по прямой линии, как это наблюдалось в случае постоянного коэффициента теплопроводности (см. рис. 3).

 Опубликовано в
Опубликовано в