Зависимость глубины залегания р-п-
 7 апреля, 2014
7 апреля, 2014  admin
admin перехода от продолжительности диффузии
Зависимость глубины залегания р — n-перехода Xj от продолжительности диффузии t для данной температуры и концентрации на поверхности Со дается выражением [76]
Х1 — А2 (Kt)'/2 Со12, (5.6)
где
K=*D, Ki/[Vq а].
|
Время проведения диффузии t, ч
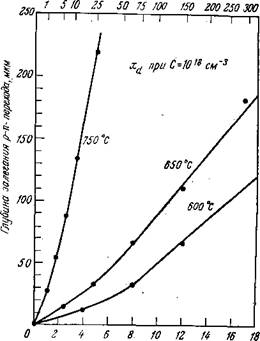
Время проведения диффузии tf^2, ч'^г Рис. 5.10. Зависимость глубины залегаиия р — /г-перехода от tl/2, где t — время проведения диффузии Zn в GaAs при 600, 650 и 750 °С [46]. |
Экспериментальные результаты, полученные для GaAs [77, 78], GaP [79], InP [80] и GaAsi_*P* [81], подтверждают эту зависимость. Зависимость х/ от t'1* линейна (рис. 5.9) [76]. Более поздние экспериментальные исследования [82], в которых в качестве источника диффузии был использован радиоактивный изотоп 65Zn, показали, что выражение (5.6) справедливо только при высоких температурах, а при температуре ниже 700 °С наблюдается непрерывное отклонение от закона х ~ /1/г с уменьшением температуры (рис. 5.10). Эти наблюдения показывают, что при данных условиях процесс диффузии нельзя описывать вторым законом Фика и что анализ по Больцману — Матано, с помощью которого находят значения эффективного коэффициента диффузии D из профиля фронта диффузии, неверен,
5.2.3. Определение коэффициента диффузии из профиля фронта диффузии
В области температур, где профиль фронта диффузии ме - няется во времени по закону
, Cx = Cs(x/(4 (5.7)
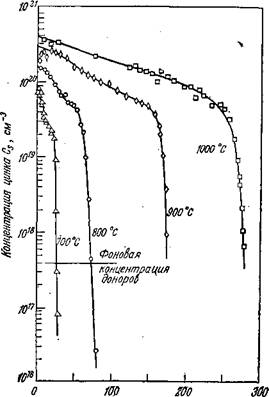
эффективный коэффициент диффузии D может быть получен с помощью анализа по Больцману — Матано [49] из экспериментальной зависимости Cs(x) (рис. 5.11). Этот метод анализа заключается в преобразовании и первом интегрировании одно-
|
ґлуіїина, мт Рис. 5.11. Распределение концентрации Zn после диффузии в GaAs при 700, 800, 900 и 1000 °С [22]. Время проведения диффузии приведено к 1,5 ч. |
мерного уравнения. Результирующее выражение для коэффициента в уравнении диффузии имеет вид
сх 1
|
Dc=- 1/(20 |
xdCsl{dCsldx)Cx. (5.8)
П J
Если продолжительность диффузии известна,- значения коэффициента диффузии D при данной концентрации цинка Сх вместе с градиентом концентрации при Сх получаются графически путем нахождения величины потока от 0 до Сх.

 Опубликовано в
Опубликовано в