Выразим параметры периодических колебаний не через длину пе­риода Т, а через обратную ей величину /Т, которая называется час­тотой периодических колебаний f и измеряется в величинах, обратных единице измерения времени. С увеличением частоты (уменьшением периода) амплитуда выход­ных колебаний уменьшается, а сдвиг Д Т выходных колебаний отно­сительно входных увеличивается. Для построения графиков, выра­жающих эти зависимости, переведем частоту / в угловую частоту <о : оз = 2л/ = 2л/Т (где п = 3,14), изліеряемую в радианах, делен­ных на единицу времен и. А сдвиг во времени между входными и выходным.

Амплитудно-частотной характеристикой системы называется гра­фик зависимости отношения амплитуд ЛЙЫХ/ЛВХ от угловой частоты <о.

Фазо-частотной характеристикой системы называется график за­висимости углового сдвига от угловой частоты со

ходиыми колебаниями выразим через угловой сдвигу = (3607Т)д7 Угловой сдвиг измеряют в градусах.

Рассмотрим пример. Для определения инерционных свойств объек­та при наладке систем управления на вход объекта подают поочередно і периодические колебания (см. рис. 13, а) с разной угловой частотой!

оэ-i, о)3, ... , <оп (рис. 14), начиная с низких частот, так что ы1<С < о>2 < й3<(1)4 и т. д. Каждой угловой частоте будет соответствовать амплитуда выходных колебаний, например Лвых1 = 44 см, Лвых2 =1 = 36 ем, Лвых3 = 12 см, Л вых4 = 12 см, т. е. с увеличением частотні амплитуда выхода уменьшается.

Вычислим для каждой угловой частоты щ, ю2, значе­ния отношений амплитуд выходных и входных колебаний. Например

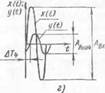
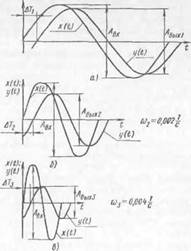
Рис. 14. Пример экспериментальной частотной ха­рактеристики для разных частот (^(а), (о2(б), o>3(e) и 0)4 (г)

Лвх= 10 т/ч. Следовательно, ЛВЫХ1/ЛВХ = 4,4 см-ч/Т; Лвых2/Лвх *=
= 3,6; Лвых3/Лвх ■= 2,2; Лвых4/Лвх = 1.2.

Нулевая угловая частота соответствует скачкообразному возмущению (см. рис. 11, а), а Лвых(0)/Лвх(0) равно установившемуся значению временной характеристики и называется коэффициентом усиления к при нулевой частоте. Зависимость отношения ЛВЬ1Х/ЛВХ от угловой частоты со называется амплитудно-частотной характеристикой системы (АЧХ) и обозначается Л (to). График амплитудно-частотной характеристики приведен на рис. 15, а.

Повторим построение ДЛЯ углов ф 2 Ифз, проводя прямые од и ое, на которых отложим отношения амплитуд, соответствующих частотам ^13ЫХ2/ЛВХ И Аьыхз/Лвх. Соединив полученные точки е, е, д> е, 0, по­лучим график АФЧХ, который для рассмотренного нами примера на рис. 16 будет полуокружностью. Если через начало отсчета провес­ти вертикальную прямую Б—Б (рис. 16, а) и прямую ОВ продлить плево (В—В), то две эти прямые разделят плоскость на четыре квад­ранта так, как это показано на рис. 16, б. Ось В—В называется ве

По мере увеличения частоты колеба­ний отставание д Т уменьшается по аб­солютной величине: Д Тг = 395 с, ДTs =

= 277 с, ДТ4 = 165 с, но относительное отставание (угловой сдвиг) увеличива­ется: <р2 = 45°; ф3 == 63е и при частоте ш4 = 0,008 1/с составляет <р4=76* (т. е.

21% от периода колебаний Т4). Зависи­мость углового сдвига <р между входными и выходными колебания­ми от частоты со называется фазо-частотной характеристикой (ФЧХ) и обозначается минус ф(со). Знак минус определяет отставание вы­ходной величины от входной. График ФЧХ приведен на рис. 15,6.

Оба графика АЧХ и ФЧХ (рис. 15) объединяют в один график амплитудно-фазовой частотной характеристики АФЧХ (рис. 16, а). Для этого на горизонтальной прямой ОВ отложим в любом масштабе величину коэффициента усиления кус. Вниз (по часовой стрелке) под углом минус ері проведем прямую ОГ. В масштабе, выбранном для /сус, отложим на прямой ОГ отношение амплитуд Л ВЫХ1/Л вх.

щественной и обозначается/^(со), а ось Б—Б — мнимой и обозначает­ся /(со).

Частотные характеристики, как и временные, позволяют опреде­лить инерционные свойства объекта, которые необходимы для на­стройки регулирующего устройства на технологический процесс. Не­правильно настроенная система регулирования может автоматически вывести технологический процесс на аварийную ситуацию (например, ззрыв технологического оборудования).

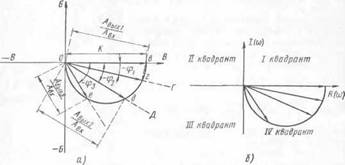
Рис. 16. Амплитудно-фазовая частотная характеристика (АФЧХ): а — графическое построение, б — квадранты плоскости