Коды, используемые для представле­ния чисел посредством числовых знаков (цифр), определяются как системы счис­ления. Наиболее употребимы позицион­ные 1 системы, запись произвольного числа А в которых при основании M ба­зируется на представлении этого числа в виде полинома:

А =Ап1Пп--Ап-1 + ... +a0m° +

+ a-.]m~'+a„2m~2+..., (1.4)

Где a, — коэффициент — один из симво­лов (цифр) системы; M — основание си­стемы; п — номер разряда 2.

При использовании системы счисле­ния основание, как правило, не пишут, а число записывают путем перечисления всех коэффициентов (символов) полино­ма: Л =a„a„_ia„_2 . . . an, a_ia_2 . . . . При этом запятая, отделяя целую часть числа от дробной, служит для фикса­ции значения каждой позиции (разряда) в последовательности цифр.

Десятичная система счисления. Это

Таблица 1.1. Характеристики систем счисления Данные различных Деся­ Изобра­ Выражение числа Систем счисления Тичное Жение Полиномом вида (1.4) Наимено­ Основа­ Алфавит Число Числа Вание Ние т (цифры)

1111 Унитарная 1 1

3 - /О3 + 7-102--0-10' + 4 • 10° + Десятичная 10 0,1,2,3,4, + 6-10~[ 5, 6, 7, 8, 9

3.S3_|_7.S2 + 0.gi_|_4.go + 6.s-i Восьмерич - 8 0,1,2,3,4,5,

Ная 6, 7

1- 53 + 3-52 + 2-51+0-5° + 3-5_1 Пятерич - 5 0, 1, 2, 3, 4

Ная

+ +0-4° + 3-4-' Четверич - 4 0,1,2,3 ная

2- 33 + 0-32+-3[ + -3° + 2-3'1 Троичная 3 0,1,2 1 .23 + 0j_22+1 -^'-fl+ 1 -2-' Двоичная 2 0,1

1.163 + 0-/62 + 7-/6'+9-/6°+ Шестнадца - 16 0,1,2,3,4, -4-8 -16~] теричная 5, _6,_7,_8j_9,

4	1111/,
3704,6	3704,6/ю
1988,75	3704,6/8
211,6	1320,3/5
120,75	1320,3/4
58,66	2011,2/3
11,5	1011,1/2
6777,5	1079,8/16

0, 1,2, 3,4,5

Система — наиболее употребляемая. Ос­нование системы — 10. В ней используют десять символов — десятичные цифры 0, 1, 2, 3, ... 9. В системе 10 единиц каж­дого разряда объединяют в одну единицу соседнего старшего разряда (выбор чис­ла 10 в качестве основания общеприня­той системы счисления исторически связан с числом пальцев на руках).

В десятичной системе последователь­ность цифр 3807,45 представляет собой сокращенную запись следующего поли­нома: 3-103 + 8-102 + 0-101 + 7-10°+4Х X Ю-1 + 5- Ю-2. В десятичной системе при обычной записи указывают только коэффициенты; при этом предполагают, что их значимость (вес) различна и оп­ределяется разрядом, занимаемым дан­ным коэффициентом (цифрой). Система является емкой, но для реализации в устройствах вычислительной техники ма­ло пригодна, так как выполнение элемен­та с десятью четко различимыми состоя­ниями представляет собой сложную тех­ническую задачу.

Унитарная (единая) система счисле­ния. Такая система имеет один цифро­вой знак (символ) — 1. Любое и только целое число в этой системе выражается набором единиц, например число 4 деся­тичной системы 1 представляется в виде 1111, число 12 —в виде 111111111111 и т. д. Система простая и легко реализу­ется (она используется, в частности, для записи заданного количества импульсов на магнитных лентах, барабанах), но является очень громоздкой. Чтобы запи­сать, например, число десятичной систе­мы 3586/ю, нужно последовательно запи­сать три тысячи пятьсот восемьдесят шесть единичных символов: 1111. . . 111. . . 1111. . . 111. . .

Другие позиционные системы счисле­ния. По принципу десятичной системы строят все другие позиционные системы счисления. В восьмеричной системе ис­пользуют восемь цифр и полином строят на основании т = 8, в пятиричной /л = 5, в четверичной т — 4 и т. д. (табл. 1.1). Если основание системы счисления боль­ше десяти, то приходится конструировать новые цифры. Так, в вычислительной тех­нике применяют шестнадцатеричную си­стему счисления с алфавитом {0, 1,2, . . ., 9, 07Т72737475Гили (0, 1, 2, . . ., 9, а, Ь, с, D, Е, f). Наличие черты над цифрой сви­детельствует о том, что численное значе­ние символа равно численному значению данной цифры плюс десять. Так, десятич­ное число 175,5/ю в шестнадцатеричной системе запишется в виде

0-161+5-16°+8-16-' = 05Ж/1б.

Двоичная система счисления. В дво­ичной системе счисления с основанием дг—2 использую? два символа — цифры

J 17

| ИНСТИТУТ |

' При необходимости выделить систему счисле­ния за написанной последовательностью цифр указывают основание системы, например 4/ю

'/2 и т. д.

!111

7.

J0 Wl II■ II « I Ера:

1 БИБЛИОТЕК** ;

1 и 0. Произвольное число в двоичной системе записывается полиномом, коэф­фициенты которого а,- могут иметь только одно из двух значений (0 или 1).

Например, десятичное число 69,5/1о в двоичной системе может быть представ­лено полиномом

1 ■ 2fi + 0 • 2й + 0 • 24- 0 • 21 - И • 22 + 0 • 21 +

+ 1 -2= I -64+ 0-32 + 0- 16 + 0-8 + 1 X Х4 + 0-2+1-1 + |.-1 = б9,5/1„)

Т. е. числом 1000101,1/2-

Система позволяет использовать при­боры и устройства с двумя устойчивыми состояниями, обеспечивает простоту вы­полнения арифметических операций и экономичность и поэтому широко исполь­зуется в вычислительной технике и авто­матике.

При необходимости в двоичной систе­ме можно представить число, записан­ное в любой другой системе [6].

Перевод чисел из одной системы счисления в другую. Наиболее прост пе­ревод чисел в двоичную систему и обрат­но из восьмеричной системы, что нахо­дит применение в устройствах вычисли­тельной техники. Чтобы восьмеричное число перевести в двоичное, надо каждую восьмеричную цифру заменить эквива­лентным ей трехразрядным двоичным числом — триадой:

Восьмеричная цифра . 0 1 2 3 Двоичное число. . . .000 001 010 011 Восьмеричная цифра 4 5 6 7

Двоичное число. . . .100 101 НО 111

Соответственно для перевода из двоичной системы в восьмеричную число нужно разделить на триады влево и впра­во от запятой и заменить триады вось­меричными цифрами. Если самая левая или самая правая триада окажется не­полной, к ней надо приписать нули.

Пример 1. Восьмеричное число 34,5/8 пе­ревести в двоичное. Восьмеричные цифры 3, 4, 5 в двоичной системе соответственно запи­шутся в виде ОН, 100, 101, тогда все число будет 11100,101/2. Нуль впереди можно опус­тить.

Пример 2. Двоичное число 11010111,110101,-2 перевести в восьмеричное:

011 010 111, 110 101 „„_„.

-о 9--------------- 7------- F------ Е =327,65/8.

Целые числа, записанные в одной системе счисления, в новую систему счис­ления переводятся последовательным де­лением числа и получаемых частных на основании той системы, в которую оно переводится, до тех пор, пока не получит­ся частное меньше основания системы. Результатом будут остатки от деления, прочитанные в порядке, обратном их по­лучению, и последнее частное.

Пример 1. Перевести число 47/ю в двоич­ное:

47 [2_

V LL ,

'Ъо'-З ^^ 2. UL

Ч"^,4' Th"^ 1 —Последнее ^^F. Частное

Таким образом, 47 m= 101111/2-

Пример 2. Перевести число 32 m в двоич-

32 LL

I*

В -

О Z^I.

-Последнее частное

Т. е. 32/ю = 100000/2.

Пример 3. Перевести число 137/т в вось­меричное:

Последнее частное

Т. е. 137/т = 211/8.

123 120 3

2_ 61 60_ 1

123 122 1

2 30 30

L 15

FlL 1

Пример 4. Перевести целое десятичное число 123 в двоичное и восьмеричное:

8 . 15 L В_ 1 7

О it 1

1 JL 1

123/, о =173/.

Т. е. 123/,o=ll 11011/2

Пример 5. Перевести целое десятичное число 691 в шестнадцатеричное:

Т. е. 691 /ю = 213

Двоично-кодированные системы счис­ления. Некоторое неудобство двоичной системы счисления заключается в гро­моздкости записи чисел. Количество цифр двоичного изображения числа при­мерно в 13,3 раза больше количества цифр в десятичном изображении того же числа. Поэтому в технике наиболее часто используют смешанные системы счисле­ния, в частности двоично-восьмеричную, двоично-шестнадцатеричную и двоично - десятичную. В этих системах объединя­ются достоинства двух систем: емкость (восьмеричной, шестнадцатеричной или десятичной систем) и двоичное изобра­жение цифр двоичной системы.

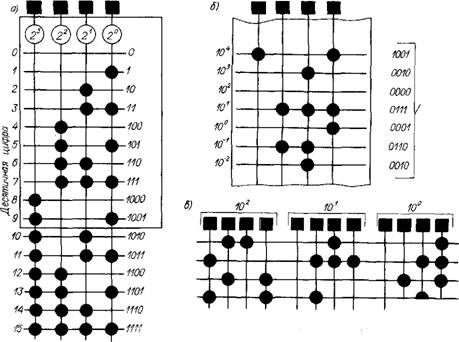
В двоично-десятичной системе каж­дая цифра десятичного числа (0, 1, 2, ... ..., 9) записывается двоичным кодом. Для этого достаточно четырех двоичных раз­рядов— тетрады (рис. 1.3). Если в си­стеме используется нормальное значение (вес) каждого разряда двоичной си­стемы, то значимость разрядов в тетраде (начиная со старшего левого) составит 23 —22 —21—2°, или 8421. В соответст­вии с этим десятичные цифры будут иметь двоичный код: 1—0001; 2 — 0010;...; 9—1001 (табл. 1.2). Для записи любого десятичного числа (более 9) на каждый разряд числа выделяется тетрада.

Так, для записи десятичных чисел от 0 до 999 необходимы три двоичные тетрады. Пер­вая (справа) определяет десятичный разряд 10°, вторая — 10', третья (слева) — 102. При этом десятичное число, например 942, будет иметь вид 1001 0100 0010 (рис. 1.3, а).

Таким образом, двоично-десятичный код является десятичным по существу и двоичным по форме представления цифр. В практике наиболее часто деся­тичные цифры в двоично-десятичном коде записывают на перфоленте строч­ками, определив для каждой из строчек определенный десятичный разряд (рис. 1.3, б).

92071,62

621 37J 505 942

Рис. 1.3. Двоично-кодированные системы счисления в представлении на перфоленте: а 8421; б, в — представление десятичных чисел в коде 8421

Д^Л - 1 Iooi Оюо1 ЧШ

Код

Двоично-десятичную систему с ука­занным выше весом разрядов называют двоично-десятичным взвешенным кодом 8421. Код этот очень удобен, но имеет недостаток: с его помощью могут быть

Таблица 1.2. Изображение десятичных чисел в системах счисления с различным основанием И О Система с основанием Двоично - ЕГ Десятичная T О Система S У 2 3 8 16 (код 8421) 0 0 0 0 0 0000 1 1 1 1 1 0001 2 10 2 2 2 0010 3 11 10 3 3 ООП 4 100 11 4 4 0100 5 101 12 5 5 0101 6 110 20 6 6 0110 7 111 21 7 7 0111 8 1000 22 10 8 1000 9 1001 100 11 9 1001 10 1010 101 12 0 0001 0000 11 1011 102 13 I 0001 0001 12 1100 110 14 2 0001 0010 13 1101 111 15 3 0001 ООП 14 1110 112 16 4 0001 0100 15 1111 120 17 5 0001 0101 16 10000 121 20 10 0001 Оно 17 10001 122 21 11 0001 0111 18 10010 200 22 12 0001 1000 19 10011 201 23 13 0001 1001 20 10100 202 24 14 0010 0000

Образованы не только цифры от 0 до 9, но и числа от 10 до 15, которые не всегда используются, и их приходится исклю­чать.

Разработано значительное число ко­дов с другими наборами весов по разря­дам: 2421; 5211; 7421 и т. д. Имеются также коды, у которых некоторые разря­ды имеют отрицательное значение веса: (6) (4) (-2) (-1); (7) (2) (-4) (-1) и др. [6, 73].

Для изображения десятичных цифр в двоично-кодированных системах счис­ления используют и комбинаторные коды: такие как 2 из 5, 3 из 5, однопеременный код Грея, двоично-десятичный однопере­менный код и др. Особенно большую роль в автоматике играют однопере - менные коды, у которых кодовое рас­стояние D между смежными комбинация­ми всюду равно 1.