Теплоотдача воды

• К практическим измерениям теплоотдачи от воды в трубах прежде всего относятся работы А. Зённекена [124]. Он исследовал теплоотдачу в трубе длиной 1,92л« идиам. 17 и 28 мм. Она была стальная с толщиной стенки 1 мм (бесшовная, цельнотянутая). Кроме того, исследовалась теплоотдача в латунной трубе диам. 17 мм. Поверхность стальной трубы по сравнению с латунной была более шероховатой. Скорости в опытах меняли в интерва­ле от 0,488 до 1,322 м/сек. Температуру стенки. определяли по температурному расширению трубы, температуру воды измеря­ли при помощи ртутного термометра. Зённекен на основе своих опытов пришел к следующим формулам:

Для стальной трубы (т. е. для шероховатой поверхности)

А = 735 • (1 +0,014 гст) ккал/м2 • час ■ °С; (362)

А0>3

Для латунной трубы (т. е. для гладкой поверхности)

А = 2020 • • (1 + 0,014 • („) ккал/м2 • час • °С. (363)

Й°. 1

В этих уравнениях /ст °С означает температуру стенки тру­бы. Эти формулы справедливы для вертикальной трубы, по ко­торой вода течет вниз. Если вода поднимается вверх по трубе, то значения коэффициентов теплоотдачи примерно на 7% меньше.

В. Штендер высказал мнение [125], что Зённекен не сумел пра­вильно определить влияние диаметра трубы и температуры во­ды и для выяснения этого вопроса поставил собственные опыты [126].

Он применил то же самое направление опыта, что и Зённе­кен,* но, кроме того, добавил вторую латунную трубку диам. 28 мм. В противоположность Зённекену он нашел, что темпе­ратура стенки трубы и особенно температура воды /„от не оказывают решающего влияния на теплоотдачу и что диаметр никак не влияет на величину коэффициента теплоотдачи. Штен­дер нашел, что коэффициент теплоотдачи не зависит от диамет­ра трубы, материала, направления движения и направления теп­лового потока (стенка — вода или вода — стенка) и выражает­ся уравнением

А = 2830(1 +0,0215 • / — 0,00007 X X /2) ш0-91 -0-00115 • *ккал/мг • час • °С. (364)

В этом уравнении I означает температуру, которая близка к средней температуре воды /пот и находится лишь в небольшой зависимости от температуры стенки. Она равна

T = ^ПОТ "4" 0,1 • (/ст - ^пот) С. (365)

Штендер в своих опытах по сравнению с опытами Зённеке - на брал значительно более высокие температуры стенки и воды, а также разности температур для того, чтобы добиться решения вопроса о доминирующем влиянии температуры стенки или воды.

Сравнение формул с

Измеренные значения
Диаметр Трубы М	Материал Трубы	* * А* Л Н О О О. О « О	Температура, °С	Коэффициент теплоотда­чи а, ккал/мгчас °С
Трубы *сТ	Воды *пот
0,0107	Медь	1,16	63,35	27,9	6310
0,0107	»	0 916	35,7	22,9	4690
0,0107	»	0,916	63.25	50,73	5860
0,0107	»	0,793	35,7	23,0	4180
0,0107	»	0,793	44,9	51,1	6930
0,017	•Сталь	0,617	30,5	19,1	2370
0,017		0,617	52,4	43,9	3200
0,017	»	0,617	62,8	46,7	3160
0,017	»	0,617	59,8	45,8	3080
0,017	»	1,322	27,5	11,4	4000
0,017	»	1,322	50,3	42,3	5470
0,017	»	1,322	67,15	58,0	5510
0,017	Латунь	0,595	30,0	38,1	3070
0,017		0,595	50,5	53,0	3600
0,017	»	0,595	50,3	63,7	3810
0,017		1,545	32,5	38,15	7150
0,017	»	1,545	26,6	36,85	6810
0,017	»	1,545	64,2	68,35	8810
0.028		0,57	20,1	13,05	2 2 60
0,028	»	0,57	53,8	18,35	2610
0,028	»	0,57	37,85	27,1	2710
0,028		0,37	16,9	13,5	1540
0,028	»	0,37	50,7	19,2	1820
0,028	»	0,37	84,5	73,45	2710
0,0124	»	0,93	104,0	32,8	4160
0,0124	»	1,64	80,0	28,4	6250
0,0124		2,27	78,4	27 1	7140
0,00159	Медь	5,40	29,4	14,4	15150
0,00159		4,30	54,0	24,0	19500
0,00159		7,50	40,9	16,8	24100
0,00159		7,94	72,1	27,6	30200
0,00159	Железо	1,94	53,4	33,2	22200
0,00159		3,61	39,3	22,5	27800
0,00159		7,26	52,5	24,3	42400

Ождение............................................................................... Ождение от значений Зённехена, Штендера, Мак А; а.......

Мак Адамс и Т. Г. Фрост [127] исследовали теплоотдачу в ла­тунной трубке диам. 12,5 мм и длиной 1,26 м, которую снаружи обогревали насыщенным паром. Температуры воды и пара из­меряли при помощи ртутного термометра, температуру стенки— припаянной снаружи термопарой. Температуры стенки доходили до 104° С и, следовательно, достигали максимального значения, исследованного до сих пор. Температура воды была всегда низ­кой, и на выходе максимальный ее показатель был равен 48,6° С, а на входе она составляла 17° С. Исследуемые скорости меня­лись от 0,93 до 2,27 м/сек. Для определения коэффициента теп­лоотдачи на участке стенка — вода была выведена следующая формула:

'{1 + ~Г-) кша/м" ■т ■ °с (366)

В этом уравнении Ь означает общую длину трубы, м; т]отн — вязкость воды при средней температуре, отнесенная к вязкости при 20° С как к единице измерения. При выводе этой формулы наряду с результатами опытов была использована теория по­добия.

Ф. К. Блейк и В. А. Питерс[128] исследовали теплоотдачу от воды в трубах очень маленьких диаметров. Для исследования использовали медную трубу с внутренним диаметром, равным

1, 585 мм, и наружным 3,18 мм, длиной 127 и 254 мм, а также железную трубу с внутренним диаметром 1,585 мм и наружным 2,8 мм. Скорость воды меняли в пределах от 1,52 до 7,93 м/сек, температуру измеряли маленькой отсасывающей термопарой, ц температуру стенки — медь-константановой термопарой. Изме­рения при всех равных условиях дали для медной трубы значи­тельно меньшее значение по сравнению с железной. Эти разли­чия в коэффициентах теплоотдачи объясняются различной шеро^ ховатостью стенок (у меди стенка более гладкая).

Необходимо теперь сравнить вышеизложенные измерения и формулы друг с другом, чтобы получить представление о том, как велика точность отдельных формул.

В табл. 14 даны особенно характерные результаты вышеопи­санных экспериментов, которые отличаются один от другого в большинстве случаев лишь скоростью и температурами. Надо стказаться от мысли охватить в этой таблице все имеющиеся измерения, однако следует отметить, что все они не имеют ни­каких систематических отклонений от результатов, приведен - я^х в таблице. Также надо сказать, что все результаты Стен­тона, Зённекена и Штендера взяты из весьма полноценного, упомянутого выше обзора, сделанного Нуссельтом.

Анализ табл. 14 (см. стр. 216 и 217) показывает следующее.

Результаты, вычисленные по формуле Л. Шиллера, расходят-’ ся с результатами измерений на 13—130%, причем каждый раз в сторону завышения. Но в соответствии с выводом формула должна была бы давать заниженные значения, так как она от* носится к случаю совершенно стабилизированного потока. Как уже кратко упоминалось выше, работа Шиллера основана на подобии скоростного и температурного полей, когда выражение

С~г*К— =)> причем для определения теплоотдачи были привле­чены результаты измерений сопротивления в трубах и связан­ное с ним образование пограничного слоя. Но, руководствуясь данными табл. 14, следует сделать вывод, что необходимо отка­заться от этих положений и что коэффициенты, полученные на основе теории подобия, все без исключения слишком неточны. Как показало сравнение с результатами измерений Штендера, а также с результатами остальных измерений, влияние диамет* ра в формуле оказалось завышенным, а влияние скорости зани­женным. Влияние же температуры, выступающей в форме теп­лопроводности под корнем четвертой степени, получается слиш­ком заниженным. Коэффициент, стоящий перед выражением, тзкже значительно занижен. Следовательно, анализ табл. 14

Х

Показывает, что постоянство критерия --------------- все-таки имеет

Ё • С - Т)

Большое значение в теории подобия [ср. уравнение (182) на стр. 100]. Напротив, как будет видно из дальнейшего, соотношение по­казателей степеней при скорости и диаметре можно почти точно определить по теории подобия даже для воды. Это очень цен­ный результат теории подобия, особенно, если учесть, что даже порядок величин, отражающих различные факторы, которые обычно принимают во внимание, в большинстве случаев также будет правильным. -

Формулы Мак Адамса и Фроста показывают значительно лучшее совпадение с результатами измерений, чем формулы Шиллера, несмотря на то что они также частично связаны с применением теории подобия и ограничены в выборе показателя степени для вязкости. По данным Мак Адамса и Фроста, вяз­кость воды необходимо брать при температуре, средней между температурой воды и температурой стенки трубы. В соответст­вии с этим формулы дают среднее расхождение на 18,9% с ре< зультатами рассмотренных измерений. С приведенными в табл. 14 результатами опытов Зённекена, Штендера, а также Мак Адамса и Фроста формулы дают расхождение на 16,6%.

Следует отметить в формулах Мак Адамса и Фроста сильное влияние на коэффициент теплоотдачи длины измерительного участка. Единицей измерения его в соответствии с законами теории подобия будет диаметр трубы. Это влияние длины, ко­торое, впрочем, было выявлено также Л. Шиллером и Т. Бур - бахом, а для перегретого пара Поензганом и для воздуха — Е. Шульце, во всех опытах не обнаруживает влияния диамет­ра; так как если длина трубы (в метрах) остается постоянной, то при измерении ее в диаметрах она уменьшается с увеличени­ем диаметра трубы, что в соответствии с уравнением Мак Адам­са и Фроста приводит к росту коэффициента теплоотдачи. Это повышение коэффициента теплоотдачи может быть компенси­ровано противоположным влиянием диаметра, так как в одина­ковых условиях опыта коэффициент теплоотдачи будет умень* шаться с увеличением диаметра. Поэтому возможно, что влия­ние диаметра трубы, выраженное степенью 0,2, в соответствии с теорией подобия было правильно определено Мак Адамсом и Фростом. Штендер же не обнаружил влияния диаметра трубы трлько потому, что длина трубы, выраженная в диаметрах, уменьшается с увеличением диаметра. Расхождение значений» вычисленных Мак Адамсом и Фростом, с измеренными величи­нами можно объяснить лишь тем, что был сделан неправильный выбор температуры. Как показал Штендер, температура жидко­сти влияет сильнее, чем температура стенки (положение, кото­рое можно подтвердить результатами измерений Мак Адамса и Фроста). Следовательно, возникает вопрос, не лучше ли совпа­дут результаты измерений, вычисленных по формуле, с резуль­татами измерений, если в качестве температуры принять вели­чину т> введенную Штендером (сравни нижеследующее). Если рассчитать вязкость по этой величине, то получим результаты Мак Адамса и Фроста, сведенные в столбец как ад^ . Эта формула весьма удовлетворительно соответствует данным из­мерений Стентона, Мак Адамса и Фроста, но большая часть остальных измерений, полученных по ней, совпадает значитель­но хуже, чем результаты, вычисленные по первоначальной фор­муле. Среднее расхождение составляет 17,6 или 16,5%. Из это­го сравнения ясно, что температурное влияние недостаточно точно определяется выражением вязкости в степени 0,8.

Формулы Зённекена дают особенно заметные расхождения в таблице в тех случаях, когда температура стенки сильно отли­чается от температуры воды. Особенно отчетливо это выявилось в измерениях Мак Адамса и Фроста, так как температуры сте­нок были высокими. Анализ близких величин по формуле Штен­дера показывает, что Штендер в своей формуле бесспорно луч­ше учел температурное влияние и потому фактически теплоот­дача от воды определяется почти всегда средней температурой воды и почти не зависит от температуры стенки. При этом не­обходимо учесть, что влияние температуры выражается в очень большом (на 72°) увеличении ее и при прочих равных условиях повышает в 2 раза коэффициент теплоотдачи. Измерения Блей­ка и Питерса дают более точное совпадение с формулами Зён­некена, чем с формулами Штендера. Это объясняется главным образом тем, что влияние диаметра трубы, которое Штендер полностью отрицает, все же существует, хотя оно настолько сла­бо, что становится заметным только при очень больших изме­нениях диаметра. Чтобы иметь право утверждать, что диаметр трубы не оказывает никакого влияния, необходимо провести опыты со значительно большим диапазоном изменения диамет­ров по сравнению с опытами Штендера (он проводил опыты с трубами диам. 17 и 28 мм). Подтверждается это тем фактом, что все формулы, приведенные в табл. 14, дают очень значи­тельный разброс по сравнению с измененными значениями и поэтому малое влияние диаметра теряется в этом разбросе, если изменения диаметра не очень значительны. Поэтому в дальней­шем следует принять во внимание противоположное влияние длины и диаметра трубы. Замечательно, что особая оценка из­мерений Блейка и Питерса дала показатель степени для скоро­сти лишь около 0,6. Сообразно с этим утверждение Стентона, что для воды показатель степени при скорости должен умень­шаться с уменьшением диаметра, подтверждается. Относитель­но расхождения формул от данных измерений Блейка и Питер­са выше уже было сказано, что полученные ими гораздо более высокие значения для железной трубы, пожалуй, объясняются ее шероховатостью, которая при малых диаметрах должна играть существенную роль. Получение значений по формуле Штендера, заниженных по сравнению с данными измерений Стентона, объясняется малой длиной трубы, взятой Стентоном, и в данном случае скорее служит признаком того, что она пра­вильнее формулы Зённекена, которая в ряде случаев дает да­же слишком высокие значения. Вообще необходимо признать формулу Штендера более точной, чем формулу Зённекена. В то время как среднее расхождение по формуле Зённекена составляет 21 и 16,3%, по формуле Штендера оно составит лишь

14,4 и 8,6%. Причина, как уже указывалось, заключается в том, что Штендер более правильно учел влияние температуры.

Упрощенные формулы. Можно, однако, доказать, что нет не­обходимости вводить вспомогательную температуру £ по Штен - деру и что практически можно достичь такой же точности, если ввести вместо нее среднюю температуру воды *пот. и совершен* но пренебречь температурой стенки это отнюдь >не противо­речит утверждениям Штендера. Формулу Штендера мо&Цо еще упростить, если принять, что показатель степени для скорости

Ре изменяется с температурой, а всегда остается равным 0,85. Ниже приведенная формула, несмотря на свою простоту, дает результаты такие же точные и даже, пожалуй, более точные,, чем формулы Зённекена и Штендера:

(367)

А = 2900 • ш0-85 • (1 +0,014 • <пот).

Значения, рассчитанные по этому уравнению, приводятся в табл. 14 в виде аш^. Они довольно точно совпадают с измерен­ными значениями, и средняя ошибка не больше, чем дает слож­ная формула Зённекена и Штендера. Только в трубах малого диаметра коэффициент теплоотдачи будет значительно меньше по сравнению с данными Блейка и Питерса. Это объясняется тем, что в уравнении (367) не учтено влияние диаметра. Так как это влияние вследствие одновременного хорошего воспро­изведения коэффициента теплоотдачи в трубе толщиной 0,028 и 0,0124 м должно быть очень незначительно, то для расчета при­нимается показатель степени, равный 0,1. Сообразно с этим уравнение (367) примет вид

А =

(368)

Если рассчитывать коэффициенты теплоотдачи, приведенные в табл. 14, по этому уравнению, то получается последний стол­бец. Видно, что для труб диаметром от 10 до 28 мм точность ре­зультатов не повышается и лишь для узких медных труб полу­ченные значения лучше совпадают с данными Блейка и Питерса. Поэтому инженеру-практику рекомендуется в целях экономии времени для расчета коэффициентов теплоотдачи воды в трубах применять уравнение (367). Лишь для труб диаметром меньше 0,5 см увеличение коэффициента теплоотдачи в зависимости от степени шероховатости может достичь 50%. С другой стороны, точное совпадение коэффициентов теплоотдачи для труб диам. 17, 24 и 28 мм показывает, что с увеличением диаметра влияние становится настолько малым, что уравнение (367) можно при­менять до диаметра величиной около 100 мм, предполагая, что - эти трубы не очень коротки. Уравнение (367) дает точное сов­падение также с результатами измерений А. П. Кольборна и О. П. Хьюгена [129].

Как показывает уравнение (366), при коротких трубах необ­ходимо вести расчет со значительным увеличением коэффициен­
та теплоотдачи. Величину до'0, необходимо брать на стр. 517 из рис. 70—72, вследствие чего уравнение (367) легко решаемся (см. числовой пример на стр. 451).

Общая формула для теплоотдачи жидкостей

Для ламинарного потока жидкостей справедливо уже приве­денное выше уравнение Кольборна для газов [уравнение (302)])

А = 1,65 • — • (—0 ‘ °р 0 У/3 ккал/м2 • час • °С. (369)

D д • L / [130]

Это уравнение, как уже объяснялось выше на стр - 180, в про­тивоположность «классическому» уравнрнию (301) Нуссельта учитывает также теплоотдачу, которая появляется дополнитель­но вследствие подъемной силы, способствующей возникновению конвективных потоков. Как установил Е. Киршбаум *, в верти­кальной трубе диаметром в свету 30 мм эти подъемные силы оказывают решающее влияние до скоростей воды 0,1 м/сек. Для важнейшего случая турбулентного потока в трубе. В. Нуссель - том [131] в 1925 г. была использована теория подобия. На основе теории подобия им было получено уравнение

A=const-~- • ^ - у ккал/м2- час • °С. (370)

В критериальной форме уравнение запишется (см. стр. 115—116)

A = const • — • (Re)n • (Pr)m ккал/м2 • час -°С. - (371)

D

По эмпирическим уравнениям автора (367) и (368) значе­ние а для воды пропорционально скорости в степени 0,85. Сооб­разно с этим в уравнении {371) показатель

П = 0,85.

Показатель т, который отражает только влияние физических величин, составляющих критерий Рг, можно отыскать путем сравнения коэффициентов теплоотдачи при различных темпера­турах. Сравнительный расчет показывает, что вследствие очень сильной зависимости вязкости воды от температуры', коэффи­циент теплоотдачи по уравнению (370) изменяется очень сильно в зависимости от показателя т, иными словами, m можно очень точно определить по данным измерений, если бы они бы­ли достаточно точны. Получается, что

Пг = 0,45.

Но так как в соответствии с положенными в основу данными измерения по табл. 14 >в среднем дают ошибку 7% с расхожде­ниями до 50%, то для упрощения берем т, равным половине, т. е.

Т = 0,5.

Если теперь определить постоянную С, то получим уравнение для коэффициентов теплоотдачи, применимое для всех жидко­стей при турбулентном потоке,

(372)

А = 0,125 • — • т0-85 • Рг'2 ккал/м2 • час • °С.

D

Критерии Рг и Ке можно взять на стр. 115, 116. Таблица 15 Сравнение формулы (372) и уравнения (368) для воды Температура воды, ®С Диаметр трубы в свету м Скорости воды, м/сек Значение а, ккал/м2 час °С Расхождение % По (372) По (368) 20 0,01 1,0 4200 3900 +7,8 50 0,01 1,0 4940 5210 —5,5 100 0,01 1,0 7150 7340 —2,5 50 0,03 1,0 4340 4890 —11,2 50 0,03 3,0 10900 12200 —10,6

В табл. 15 приведены для сравнения характерные точки, определенные по различным формулам. Очевидно, что темпера­турная зависимость передается через Рг[132]1 очень слабо. Через Рг°'*° она будет передаваться несколько лучше. Но так как разница между полученными в том и другом случаях значени­ями лежит в пределах допустимой ошибки, то необходимо вы­брать более простой показатель степени, т. е. Уг - В остальном расхождения между результатами, полученными по этим фор­мулам, довольно малы, так как разница между показателями степени составляет всего лишь 0,5—0,45 = 0,05. *

Теплоотдача масел

При турбулентном потоке для масел всех сортов также спра­ведливо уравнение (372). Для ламинарного движения масел из­мерения провел Г. Крауссольд *. Он исследовал теплоотдачу ма­сел в медных и латунных трубах диам. 40, 26, 16 и 10 мм. Трубы имели длину 3 м, причем для трубы диам. 40 мм первые 2 м счи­тались начальным участком. Однако оказалось, что такая длина начального участка далеко не достаточна, чтобы получить посто­янное температурное поле и стабилизированный ламинарный по­ток. Следовательно, опыты проводились в области нестабилизи - рованного ламинарного потока, который преимущественно и встречается на практике. Вследствие этого скорость еще оказы­вала влияние.

В большинстве случаев масло имело температуру 80°; темпе­ратура стенки между 30 и 60°. Один раз были сделаны из­мерения в трубе диам. 40 мм с более низкой температурой мас­ла (30еС) и высокой температурой стенки (65° С). Скорость

Физические свойства относятся к средней температуре жидкости. В каче­стве линейного размера принят гидравлический диаметр. Это уравнение спра­ведливо для любых упругих ^и капельных жидкостей независимо от темпе­ратуры, температурного напора, давления, тепловой нагрузки и направления теплового потока. Исключением является узкая область температур изме­нения фазового состояния пара, когда происходит резкое изменение его фи­зических свойств.

Закономерность теплоотдачи при ламинарном движении в трубах выра - з&ается уравнением (</?е<2000)

Prm -25

Nu = 0,15 • Яе0’33 • Pr°>43 [-^“j0’25 ' G2''

В этих формулах влияние формы сечения учитывается эквивалентным диа­метром, влияние физических свойств жидкости—критерием Прандтля, влия­ние температурного напора и направления теплового потока параметром

, влияние подъемной силы—критерием Грасгофа и влияние ре-

Жима движения (скорости)—критерием Рейнольдса.

Таким образом, формулы М. А. Михеева являются более универсаль­ными по сравнению с формулами Нусоельта, Мак-Адамса и Крауссольда, а также др. ~

Применительно к воздуху (или какой-либо другой среде) можно полу­чить частные более простые расчетные уравнения. Например, поскольку для

Рг ж

Воздуха Pr—0,7=const, а —— =1, то для теплоотдачи при турбулентном

С

Движении получим уравнение А^=0,018. Re0’8.

Подробно см: М. А. Михеев, Сб: «Теплопередача и тепловое модели­рование», АН СССР, 1959.

Литература в сноске * на стр. 181. (Прим. ред.).

* К г а u s s о 1 d, H., Die Wдrmeьbertragung bei Zдhen Flьssigkeiten. VDI — Forachungsheft 351 (1931). Здесь же дана литература по этому вопросу.

Масла бралась в пределах 0,06—2,4 м/сек. Было иоследовано масло двух различных типов, одно из которых вязкое (машин­ное) и другое мало вязкое (трансформаторное). Для области, где отсутствует турбулентное движение (ниже /?е=2300), Кра - уссольд нашел следующую формУлу:

А = 11,5 - — - Ре0,23 • 1 / — ккал/м2 • час • °С, (373)

С1 У Ь

Где Ре — критерий Пекле, равный а) С' ^

^сек

Т — скорость, м/сек; й — диаметр трубы, м

Ь — длина трубы до места измерения, м

X— коэффициент теплопроводности, ккал/м • час • °С;

Хсек — коэффициент теплопроводности, равный Х/3600, ккал/м• сек-0 С.

Так как показатели степени 0,23 и 0,27 практически близки к лег­ко рассчитываемому корню четвертой степени (0,25), то рекомен­дуется уравнение (373) пересчитать на этот показатель. К сожа­лению, область, измеренная Крауссольдом, недостаточно велика, чтЬбы путем измерений четко выявить влияние температуры, как это было представлено в уравнении (373). Так как коэффициент теплопроводности довольно сильно уменьшается с повышением температуры, то рост температуры должен вызывать существен­ное уменьшение и коэффициента теплоотдачи. И действительно, измерения шестой серии, проводимые с холодным маслом (29°) и в обогреваемой трубе (64°) дали более высокий коэффициент теплоотдачи,, чем при горячем масле. Но, к сожалению, в этом опыте тепловой поток был направлен в противоположную сто­рону по сравнению с остальными опытами, так что влияние тем­пературы масла выяснено еще не до конца. Оценка измерений Крауссольда для нестабилизированного (возмущенного) лами­нарного движения масел дает следующую формулу:

О;0’25

А = (62 — 0,23 • ^) *------------- ккал/м2 • час • °С, (374)

£*0'25 - УТ

Где Ь — длина трубы на участке от начала до середины трубы в опытах Крауссольда, т. е. Ь = 1,52 м. Результаты, полученные по уравнению (374), довольно точно совпадают с данными измере­ний Крауссольда, проведенных как для машинного, так и для трансформаторного масла. Подтверждается это и тем фактом, что коэффициенты теплопроводности обоих масел практически рав­ны и зависимость их от температуры одинакова. Следовательно, уравнение (374) для других масел также должно давать пра­вильные значения. Значительное влияние длины трубц в форме корня второй степени необходимо объяснить тем, что речь идег о

Завихренном потоке. С увеличением длины трубы поток успокаи­вается, вследствие чего коэффициент теплоотдачи будет умень­шаться. Следовательно, уравнение (374) справедливо лишь для ламинарной области на начальном участке. Для образования стабилизированного ламинарного потока и соответствующего температурного поля необходим участок длиной около 50 м при диаметре трубы 40 мм•

По уравнению Нуссельта (301) коэффициент теплоотдачи при чисто ламинарном, успокоенном потоке составляет приблизи* тельно всего лишь!/б коэффициента теплоотдачи, который полу­чается по уравнению (374) при практически применяемых зна­чениях длины труб.

При /?е>2300 происходит {переход в турбулентное движение, и коэффициент теплоотдачи сразу повышается приблизительно на 50%.

Крауссольд, руководствуясь указаниями Меркля, дает для воды удачную формулу с дополнительным коэффициентом, приб­лизительно равным 0,05. Такой коэффициент взят потому, что масло имело коэффициент теплоотдачи, равный приблизительно 5% от коэффициента теплоотдачи для воды. Однако этот коэф­фициент должен быть различным для различных видов масел. Если положить в основу формулу (367) для воды, то коэффици­ент теплоотдачи при турбулентном движении масел составил бы

А = С ■ 2900 • ш°*85 • (1 + 0,014 • 0 ккал/м2 . час • °С. (375)

При С = 0,05 было бы, следовательно,

(376)

А = 145. ш0-85 - (1+0,014 • і).

Уравнение (376) дает результаты, удовлетворительно совпадаю^ щие с двенадцатой серией опытов, проведенных Крауссольдом с трубой диам. 26 мм. Напротив, например, результаты опытов девятой серии, проведенных с трубами диам. 16 мм, плохо сов­падают,-котя речь идет о том же самом масле [уравнение (376) дает здесь значение, завышенное приблизительно на 50%]. Для трансформаторного масла по уравнению (376) получают коэф­фициент, равный приблизительно половине измеренного значе­ния. Таким образом, в качестве окончательной формулы для вязких масел применимо уравнение (376), а для маловязких масел

А =300 • ш0,85 • (1 + 0,014 • і) ккал/м2 • час • °С.

В соответствии с вышесказанным Крауссольд установил, что, как и для воды, решающее влияние на коэффициент теплоотда - 15*
чи и соответственно на выбор физических величин оказывает средняя температура масла, а не температура стенки. Поэтому в уравнениях (374) — (377)/—есть средняя температура масла. Обобщая, можно сказать, что для масла, протекающего на на­чальном участке ламинарно, уравнение (374) дает, по-видимому, достаточно точные значения коэффициента теплоотдачи, в то еремя как для турбулентно движущегося масла уравнения (375) — (377) еще не дают удовлетворительных результатов. Поэтому лучше рассчитывать теплоотдачу для турбулентно дви­жущихся масел по уравнению (372).

Теплоотдача жидких металлов

Этот случай теплоотдачи играет большую роль в ртутных па­ровых котлах и в будущем, вероятно, будет играть большую роль В атомной энергетике. Измерения проводили со ртутью, причем К. Эльсер [133] обращает внимание на затруднение, возникающее из-за того, что ртуть в большинстве случаев не смачивает стен­ки. Поэтому Р. Е. Лайон [134] провел опыты с легкоплавкими спла­вами калия и натрия, которые хорошо смачивают стенки, сде­ланные из чистого никеля. Жидкие металлы отличаются от обычных жидкостей тем, что коэффициент теплопроводности их очень высок, в то время как удельная теплоемкость и вязкость малы. Поэтому выражение

Pr= - ОH2L

Хсек

Для жидких металлов в 20—30 раз меньше, чем для обычных жидкостей. Этот вид теплопередачи необходимо особенно тща­тельно исследовать. К. Эльсер проводил расчеты теплоотдачи от подобного вида жидких сред и нашел, что формула

А = -А [7 + 0,025 • (Re • Рл)0,81 ккал/м2 • час -°С (378)

D

При произведении Re • Рг>1000 очень хорошо совпадала с его теоретическими результатами; при меньших значениях произве­дения Re*Pr измерения отклонялись от результатов, получен­ных по формуле, приблизительно на 30%. Если написать произ­ведение Re »Pr в развернутом виде, то сомножитель g-rj сокра­щается и получится

Re • Pr = - d ' ш ‘ I-. (379.)

_____________ Хсек

Это не что иное, как критерий Пекле. В его выражение не вхо­дит вязкость.

Следовательно, коэффициент теплоотдачи от жидких метал­лов запишется проще

Сс = — ♦ (7 + 0,025 • Ре0'[135]) ккал/м2 • нас *°С. (380)

Й

Если уравнение (380) записать в развернутом виде и учесть, что Хсек —Х/3600, то для теплоотдачи жидких металлов к омы­ваемым стенкам получим

(381)

А== 7--------- у 17,5 • —----- c°‘V’8 ч°,6ккал/м2-час°-С.

D а*'* 1

У металлов, которые не смачивают стенку трубы, значение а по Эльсеру должно быть меньше. Как видно из формулы, коэф­фициент теплоотдачи для жидких металлов характеризуется ог­ромной величиной, так как лишь первое слагаемое уравнения для^ ртути, например, которая отличается чрезвычайно низким коэффициентом теплопроводности, в трубе диам. 200 мм дает значение 3100 при скорости, равной нулю.

Р. У. Кин *, исследуя теплоотдачу от жидкого цинка к графи­товым стенкам, прежде всего хотел определить стойкость гра­фита. После 50-часового опыта при температуре 1500° С он не обнаружил никаких повреждений. При Яе = 40000 им было най­дено, что коэффициент теплоотдачи от жидкого цинка к графито­вой стенке составил 30000 ккал/м2 • час • °С.

Г. Бюлер"[136] исследовал теплоотдачу от жидкого свинца на по­груженный в него только что обточенный стальной цилиндр диам. 17 мм, причем температура свинцовой ванны в первом опы*- те была равна 450°, а во втором 750° С. Количество воспринятого тепла определялось по наклону кривой разогрева стального ци­линдра. При температуре ванны 450° получился коэффициент теплоотдачи а = 1112, а при 750° а = 1075 ккал/м2 • час*°С.

Из этого следует, что коэффициент теплоотдачи в спокойной свинцовой ванне почти не зависит от температуры ванны и со­ставляет круглое значение 1100 ккал/м2 • час • °С.

Видимо поэтому (пи = 0) уравнение (381) имеет слишком вы­сокие показатели. При преобладающем влиянии процессов теп­лопроводности но сравнению с конвекцией влияние диаметра в действительности должно быть меньше, чем это следует из урав­нения (381) во всяком случае тогда, когда речь идет о потоке не в трубе [137].

Теплоотдача при кипении жидких металлов

Р. Е. Лайон, А. С. Фауст и Д. Л. Катц [138] исследовали теплоот­дачу при кипении жидких металлов. Это представляет интерес в тех случаях, когда желательна особенно высокая удельная теп­лопередача (ккал/м2 • час). В опытную установку входил неболь­шой котел, который состоял из отдельных горизонтальных труб из нержавеющей стали диам. 3Д дюйма с электрическим обогре­вом. Над ним был расположен трубчатый конденсатор с ребра­ми, охлаждаемый воздухом. Для защиты от влаги в аппаратуру вводили сухой азот.

Коэффициенты теплоотдачи измеряли при кипении чистой ртути, ртути с добавкой 0,1% натрия, ртути с добавкой 0,02% магния и 0,0001% смеси титана, натрия, натрия-калия (№К), а также кадмия при атмосферном давлении и температуре между 350 и 900° С. Для сравнения в этой же аппаратуре измеряли ко­эффициент теплоотдачи для кипящей воды.

Значения а для чистой Н£ (так же, как и для Сс1), несмотря на высокий температурый перепад (до Ы — 500° С), были низ­кими и уменьшались с повышением А/, что указывает на чистое" пленочное кипение. При добавке 0,1% Иа значения а были вы­ше приблизительно в десять раз по сравнению со значениями, получаемыми при добавке чистой Н£. Максимальное значение

Было достигнуто при А/ = 6..................... 7° С. Оно составило

15000 ккал/м2 • час • °С.

При более высоких значениях появляется пленочный ре­жим кипения с меньшими значениями а. При добавке 0,02% Мд и 0,0001% "П коэффициент теплоотдачи достигал 45000 ккал/м2 • час *°С при = 6... 7°С. Переход от пузырьково­го кипения к пленочному здесь не наблюдался. Разумеется про­изводительность конденсатора была ограничена. Максимально­го значения а достигал при добавке Иа и ИаК До 75000 ккал/м2 • час • °С при = 5...6 °С.

Малый коэффициент теплоотдачи для чистой ртути, очевидно, можно объяснить той же самой причиной, которая привела к малому коэффициенту теплоотдачи конвекцией ртути, а именно тем, что ртуть не. смачивает стальные стенки. Поэтому для изу­чения теплоотдачи в стальных трубах ртуть надо применять ос­торожно [139].

Теплоотдача насыщенных ларов в корне отличается от тепло­передачи конвекцией в газах. Как только насыщенный 'пар соп­рикасается с поверхностью, которая холоднее его, происходит Конденсация и свободно выделяющееся значительное количест­во тепла переходит на холодную поверхность. Одновременно на поверхности охлаждения образуется пленка жидкости, кото­рая несколько задерживает передачу тепла. Толщина этой плен­ки оказывает решающее влияние на теплоотдачу пара, так как вследствие ламинарного потока тонкой пленки тепло через нее может быть передано лишь теплопроводностью, а коэффициент теплопроводности воды и других практически применяемых жидкостей мал. Пленка будет тем толще, чем медленнее может стекать образующаяся вода. При прочих равных условиях вода стекает тем медленнее, чем больше положение поверхности наг­рева отклоняется от вертикали. Конечно, при вертикальных тру­бах или стенках пленка жидкости в нижней части всегда будет более толстой, потому что туда сверху стекает вновь образовав­шаяся жидкость. Поэтому при вертикальных поверхностях коэф­фициент теплопередачи конденсирующегося пара в нижней ча­сти уменьшается, и делать слишком высокими вертикальные по­верхности, воспринимающие тепло, не рекомендуется. Скорость стекания зависит от вязкости жидкости: чем она меньше, тем быстрее стекает жидкость и тем тоньше будет пленка конденса­та. Так как вязкость у всех практически применяемых жидкостей уменьшается с повышением температуры, то коэффициент тепло­отдачи для конденсирующегося пара при прочих равных услови­ях с повышением температуры должен увеличиваться. В качест­ве расчетной температуры можно взять среднее арифметическое значение из температур поверхности нагрева и пара. Наконец, толщина пленки жидкости зависит от степени шероховатости по­верхности нагрева. Чем более шероховата поверхность, тем тол­ще должна быть пленка конденсата вследствие заполнения жид­костью углублений поверхности.

Эти положения относятся к пару, находящемуся в спокойном состоянии. Если же пар имеет собственное движение (по Нус-

Сельту скорость его более 1 м/сек)*, то оно влияет на движение пленки жидкости. Следовательно, поверхность нагрева должна быть расположена таким образом, чтобы движущийся пар уско­рял стекание конденсата, а не замедлял его противоположным направлением движения.

Кратко изложенные выше условия теплоотдачи конденсирую­щихся паров были исследованы и математически обработаны В. Нуссельтом в его классической работе**.

При составлении своих уравнений он исходил из следующих положений.

1. Тепло, отдаваемое паром, может быть лишь теплом кон­денсации, потому ччто поверхность жидкостной пленки, обращен­ная к пару, должна иметь температуру пара. Поэтому теплопе­редача путем конвекции и излучения невозможна.

2. Вследствие малых скоростей потока и малой толщины плен­ки конденсат движется ламинарно, поэтому передача тепла че­рез него может осуществляться лишь путем теплопроводности, а не конвекции и определяется обычными законами теплопро­водности.

3. Толщину »пленки в каждой точке можно определить по средней скорости потока и по количеству протекающего череа поперечное сечение пленки (конденсата.

4. Скорость отдельных слоев пленки устанавливают из ус­ловий равновесия сил трения и веса пленки.

5. Количество конденсата определяют по количеству прохо­дящего тепла* а последнее — исходя из толщины пленки и раз­ности температур поверхности нагрева и пара — по законам теп­лопроводности.

Основываясь на этих положениях, Нуссельт вывел следующие уравнения.

Коэффициент теплоотдачи спокойного, свободного от воздуха насыщенного пара на вертикальную стенку в точке, располо­женной на расстоянии хм от верхнего края стенки, отнесенный к 1 сек., равен

Г

------- сек------------ ккал/м? ■ сек • °С. (382}

4 • Т) • х • (/Пар — ^ст)

Средний коэффициент теплоотдачи аср для вертикальной стен­ки высотой Н м равен

________ . - т V -;:&£*• ■ <з8з>

* По данным русских исследователей скорость движения пара влияет на процесс теплообмена при значениях, превышающих 10 м/сек (см. М. А. Ми­хеев, Основы теплопередачи, ГЭИ, 1956). (Прим. ред.)

** Nusselt, W., Die Oberflachenkondensation des Wasserdampfes. 2L VDI, 60 (1916), S. 541/46.

Где г —теплота конденсации при температуре пара, ккал/кг [140];

7 —удельный вес пара, кг/ж3;

КеК — коэффициент теплопроводности, ккал/м2сек °С[141];

Т] — вязкость, кг • сек/м2;

*пар — температура пара *, °С [142]; tcт —температура стенки, °С.

Формулы справедливы также для вертикально расположен­ных труб; если их диаметр не очень мал. При малых диаметрах (например, несколько миллиметров) коэффициент теплоотдачи, отнесенный к величине поверхности нагрева, будет меньше, чем получается по уравнениям (382) и (383).

В уравнениях (382) и (383) все физические величины явля­ются функциями температуры. Поэтому совершенно аналогич­но тому, как это сделано в формулах, полученных с помощью теории подобия в разделе II, для каждого вещества их можно выразить определенной температурной функцией. Если значе­ния т|, р, / и у для различных температур подставить в уравне-

/ооо 4 / г • 72 •

Ние (383), то для выражения |/ —1----------------- получим кривую,

У 4*7]

Которая с допустимым приближением мажет быть заменена прямой, определяемой уравнением

Г-~£^ = 1.21 + 0,0095 • 4Р - (384)

Коэффициент теплоотдачи от насыщенного пара, свободного от примеси воздуха, к вертикальной стенке высотой А м соот­ветственно будет равен

Асек. ср == • (1,21 -}- 0,0095 • /Ср) X

О

XI/ —:— --------------- ккал/м2 • сек • °С. (385)

У Л(*пар-*ст)

Здесь /ср °С — средняя величина между температурами па-

. ^пяп “I - ^СТ

Ра и поверхности нагрева, следовательно /ср = ----------------- ^--------

Кроме того, принято коэффициент теплоотдачи относить не к 1 сек., а к 1 часу. Поэтому уравнение (385) необходимо умно­
жить на 3600. Получается средний коэффициент теплоотдачи от водяного пара'[143] к вертикальной стенке высотой Л м:

Ккал/м2-час-°С.

5800 + 23(/Пар + <ст) }/" к • (/пар )

(386)

Аср

Кривая для значения корня четвертой степени дана на рис. 70— 72 (см., стр. 517—519). Из уравнения (386) можно определить, например, средний, коэффициент теплоотдачи от спокойного на­сыщенного пара к поверхности вертикальной трубы высотой, Г. и при давлении пара 0,1 ата, температуре пара 46°С, температуре стенки /ст = 40°С:

А = -5800 + 23 = 4960 ккал! м2*час. • °С.

4/—

V б

Из уравнений (385) и (386) видно, что влияние температуры па­ра или, что для насыщенного пара то же самое, влияние давле­ния пара очень велико.

При увеличении температуры от 20°С (что соответствует 0,024 ат) до ]45°С (что соответствует 4,24 ат) коэффициент теп­лоотдачи удваивается.

При более высоких температурах результаты, вычисленные по уравнениям (385) и (386), расходятся с расчетными значе­ниями Нуссельта, а именно, при 160°С они будут выше по срав­нению с указанными Нуссельтом в табл. 3 значегиями на 35%. Причина расхождений пока не выяснена [144]. При решении урав­
нения (386) предлагается применять значения, приведенные в табл. 16.

Таблица 16 Физические характеристики воды Температура °С Коэффициент X теплопроводности ' ккал/м сек. °С Удельный вес 7» кг/м* Скрытая теплота конденсации г ккал/кг Вязкость?}, кг-сек/м* 0 1,322- 10-4 999,9 594,7 1,815-Ю-4 30 1,441 • 10~* 925,7 578,8 0,803-Ю-4 60 1,560-10-4 983,2 562,4 0,483-10—4 100 1,718-Ю-4 958,5 539,1 0,302-Ю-4 160 1,955-10“4 907,5 498,9 0,175-10~4

Для паров бензола под давлением 1 атм Нуссельт нашел:

Аср — —----------------- ккал/м2-час • °С. (387)

/Л (^пар — ^ст)

Для паров спирта при давлении 1 атм

Ас р = —----------------- ккал/м2* час-°С. (388)

V Ь (^пар — ^ст)

Для горизонтального расположения трубы, вследствие изменив­шихся условий стекания конденсата, формулы получились иные* чем для случая вертикального положения. Для соотношения коэффициентов теплоотдачи вертикально расположенной трубы авеРт и трубы, расположенной горизонтально, агориз Нус­сельт вывел следующую формулу:

Агориз =077()*/~±_ (389>

Аверт У &

Если в это уравнение подставить значение аверт из уравнения (386), то получим следующее выражение для коэффициента
теплоотдачи от конденсирующегося водяного пара к горизон­тально расположенной трубе:

Ккал/м2 • час • °С.

4460 + 17,7 (/пар - г/ст) V d (/пар — ^ст)

(390)

Агориз

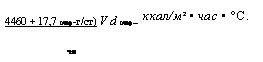Сообразно с этим лишь для трубы, диаметр которой равен ее длине, .коэффициент теплоотдачи при горизонтальном положении будет меньше, чем при вертикальном; для нормальной же тру­бы, длина которой^значительно превышает ее диаметр, этот ко­эффициент будет более высоким. Например, для трубы длиной 1 м и диам. 0,02 м при горизонтальном расположении по урав­нению (389) получится

Агориз == аверт [145] 0,770 • |/ 50 — 2,05 • осверТ.

Согласно формуле Нуосельта, 60% конденсата образуется в верхней половине трубы, а 40% — в нижкей при ее горизон­тальном положении.

Чтобы эта формула Нуссельта была справедлива, принима­ем, что конденсат стекает равномерно и не образует капель. Ес­ли это произойдет, то коэффициент теплоотдачи должен повысить­ся, так как уменьшится толщина пленки жидкости. И наоборот, нельзя полностью удалить пленку, так как в точках, где пленка отсутствует, немедленно начнется интенсивное образование кон­денсата. Е. Шмидт установил и подтвердил фотографиями, что фактически на гладких поверхностях происходит образование капель конденсирующегося водяного пара. Следовательно, уравнения (383) — (390) дают минимальные значения коэффи­циента теплоотдачи. При давлении, равном 1 атм, уравнение (386) при разности температур между стенкой я паром в Ш°С дает коэффициент теплоотдачи а = 5650 ккал/м2-час°С. В качест­ве опытной величины следует принять а = 10000 ккал/м2»час-°С; следовательно, уравнение (386) дает слишком малое или, вернее, минимальное значение коэффициента. Однако, принимая во внимание сказанное выше, уравнение (383) можно использо­вать для неисследованных еще конденсирующихся паров.

В подробной работе Е. Киршбаум и егъ соавторы * исследо­вали теплоотдачу перегретого и насыщенного паров при пле­ночной и капельной конденсации и различных скоростях движе­ния пара. При пленочной конденсации получилось довольно точ­ное совпадение с теорией Нуссельта. В противоположность гос-
по д ств'ов а в шему ранее мнению (особенно р аспростратгетгн ому на сахарных заводах) автор считает, что перегретый пар обеспе­чивает более высокую теплоотдачу (в ккал/м2 • часС), чем на­сыщенный пар такого же давления. Лишь при очень высоких ско­ростях насыщенный пар имел небольшое преимущество. Перег­ретый пар при разности температур между паром и стенкой М = ГС передает по сравнению с насыщенным паром в 2 раза большее количество тепла. Начиная от перепада 1Д/ = 4°С пар обоих видов дает практически одинаковое количество передава­емого тепла. Естественно, коэффициент теплоотдачи от перегре­того пара намного меньше, чем от насыщенного, так как здесь речь идет об удельной теплоотдаче в ккал/м2 • час, а не о коэф­фициенте теплоотдачи. Другими словами, преимущество пере­гретого пара относится к количеству передаваемого тепла, а не к коэффициенту теплоотдачи.

Капельную конденсацию осуществляли вдуванием в подво­дящий паропровод малого количества паров стеаринового мас­ла. При такой капельной конденсации коэффициент теплоотдачи возрастал приблизительно в 3,5 раза по сравнению с пленочной конденсацией, исследованной Нуссельтом. По сравнению с пе­регретым паром (300°С) результат получился приблизительно на 25% выше. Скорость пара влияла незначительно.

Из этих результатов следует, что теория Нуссельта дает ми­нимальные значения коэффициента теплоотдачи, которые в боль­шинстве практических случаев будут увеличиваться за счет частичной капельной конденсации.

В. Г. Мак-Адамс и (Т. Г. Фрост[146] продолжили изучение теп­лоотдачи различных паров, в частности определяли коэффици­енты теплоотдачи от паров воды, бензина и четыреххлористого углерода. Опыты осуществляли так: пар проходил через коль­цевое пространство, образованное двумя концентрически рас­положенными трубами, а охлаждающая вода протекала по внут­ренней трубе. Поток охлаждающей воды двигался под дейст­вием силы тяжести. Температуру воды и пара измеряли ртут­ным термометром, а внутреннюю температуру — термопарой. Длина трубы в этом опыте составляла 1,2 м, внутренний диаметр наружной трубы (железной) был равен 38 ммщ внутренний диа­метр внутренней трубы (латунной) 12,5 мм, толщина стенки внутренней трубы 2,34 мм. Ценность измерений, к сожалению, снижается из-за того, что исследователи не указали, каково бы­ло положение трубы: вертикальное или горизонтальное. Ре­зультаты измерений даны в табл. 17.

Таблица 17 Теплоотдача от конденсирующихся паров Температура пара, °С Пар—стенка Температура охлаждающей воды, °С Скорость охлажде­ния воды м/сек Коэффипиент теплопередачи стенка — вода ккал/м[147] час - .ос > Разность темпера­тур, °с Коэффициент Теплоотдачи Вход Выход Измерен­ Ный Рагсчитан - пы# по уравнению (390) Вход Выход Ккал/м* •час °С Водяной пар 100,6 98,0 19,3 10700 10070 19,0 37,8 1,640 6250 101,0 98,5 20,6 10300 9900 19,1 34,2 2,100 63Г0 106,4 114,0 23,7 10100 9740 19,1 35,4 2,180 6940 102,0 99,0 22,1 10500 9750 19,5 34,7 2,270 7140 117,0 115,0 12,0 16400 12450 17,0 48,6 0.9Г0 4160 100,3 99,0 13,4# 11300 112С0 17,3 39,8 1,010 3940 99,5 98,8 12,4 12100 11410 17,0 40,0 0,975 3860

Четырсххлористый углерод 77,2 I 73,0 I 14,8 I 1382 I — I 19,5 I 38,5 I 0,160 I 956

Пары бензина 80,4 76,4 15,5 1495 — 19,5 42,2 0,152 1060 80,8 77,0 12,6 1790 —’ 19,3 42,2 0,146 915

Если опыты проводили при горизонтальном положении тру­бы, то результаты измерений и расчетов совпадали очень точно.

Небольшое загрязнение поверхности теплопередающей тру* бы привело к заметному ухудшению теплопередачи, чего и сле­довало ожидать, согласно рассуждениям на стр. 42, вследствие высоких значений коэффициента теплоотдачи.

Дальнейшие практические измерения теплопередачи и изу­чение вопроса, вызывает ли малый перегрев пара ухудшение теплопередачи конденсаторов, провели Л. А. Приджен и В Л* Беджер *. Они нашли для испарителя (трубы внешним диам. 22 мм и внутренним—12 мм) коэффициенты теплоотдачи, при­веденные в табл. 18.

Коэффициент теплопередачи & в обоих случаях, кроме тем­пературы пара, зависит от режима кипения воды. На основании сделанных наблюдений установлено, что к растет с увеличени­ем количества конденсата. При этом должно усилиться кипение й, следовательно, повысится коэффициент теплоотдачи на сто­роне воды. Достоин внимания тот факт, что слабый перегрев пара от 20 до 20° С не оказал заметного влияния на теплопере­дачу. Это практически совпадает с наблюдениями Киршбаума.

Вопрос — перегретый или насыщенный пар вызывает более высокую теплопередачу — для большинства случаев можно ре­шить и без точного знания коэффициентов теплоотдачи путем выбора коэффициента теплопередачи, приведенного на стр. 42—43.

Таблица 18 Коэффициенты теплопередачи пар — вода Температура кипящей воды, °С Температура пара °С Коэффициент теплопередачи ккал/мм2 • нас °С Новая железная труба 75 110 3100 75 85 1585 Полированная медная труба Ч 75 86,0 3870 75 113,7 10400 Медная Труба мал о з а гря зненна я 75 83,7 1300 75 107,1 5500

Сообразно с этим перегретый пар всегда обеспечивает более высокую теплопередачу, чем насыщенный, если тепловое сопро­тивление на участке перегретый пар — стенка характеризуется наибольшим удельным весом в тепловом потоке. Так, например, комнатные обогреватели с перегретым паром всегда отдают большее количество тепла, чем с насыщенным того же давле­ния, так как в этом случае сопротивление теплопередаче на участке «обогреватель — воздух» так велико, что коэффициент теплопередачи вследствие более низкого коэффициента тепло­отдачи перегретого пара по сравнению с насыщенным будет уменьшаться незначительно, в то время как более высокая тем­пература перегретого пара вызовет соответствующее повышение теплопередачи. В этих случаях температура стенки лежит вы­ше конденсации перегретого пара.

М. Якоб и С. Эрк также нашли, что конденсирующийся пе­регретый пар в общем отдает большее количество тепла на по­верхность определенной температуры, лежащей ниже точки насыщения, чем насыщенный пар того же давления.

При малых же тепловых сопротивлениях конденсирующийся насыщенный пар, естественно, создает значительно более вы­сокую теплопередачу, чем (перегретый неконденсирующийся. Если известны коэффициенты теплоотдачи, то вопрос всегда можно решить путем расчета коэффициента теплопередачи [148].