Вынужденный поток газов
 20 мая, 2013
20 мая, 2013  admin
admin Теплоотдача в трубах при турбулентном потоке
Теплоотдача в трубах является важнейшим видом теплопередачи и поэтому ее так много исследовали. Но измерить коэффициент теплоотдачи от газов в трубах при более высоких температурах особенно трудно, так как газовый поток нарушается измерительным прибором и точно измерить температуру газа обычными средствами невозможно вследствие лучистого обмена измерительного прибора с окружающей средой. К тому же затруднения вызывает и, определение средней температуры газового потока по одной температуре, измеренной, например, по оси, вследствие чего коэффициенты теплоотдачи, найденные различными исследователями, не совпадают один с другим. Поэтому до сегодняшнего дня остается спорным вопрос о влиянии температуры газа на теплоотдачу конвекцией в трубе. В дальнейшем необходимо выяснить этот вопрос, опираясь на все известные в настоящее время важные измерения, и дать новые значения постоянных коэффициентов *.
Г. Гребер[70] исследовал теплоотдачу от воздуха при температуре 90—330° С, протекающего в бесшовной стальной трубё диам. 62 мм. При этом темвдратура стенки колебалась, в интервале от 60 до 250° С. Скорость воздуха, отнесенная к нормальным условиям (0°С, 760 мм рт. ст.), была установлена от 2 до 10 м/сек[71]. Особо тщательно Гребер проводил измерение тем
пературы воздуха, что выполнял с помощью термопар, защищенных от излучения трубкой. Их показания проверялись дополнительно особым опытом или повторным измерением. Поэтому эти измерения надо считать первыми, 1ПО которым достаточно точно можно было обнаружить влияние температуры. Защищенные от излучения термопары несколько нарушали поток. Хотя Гребер и. проводил свои опыты на участке успокоения, но формя потока, пожалуй, не очень-то отличалась от начальной фо»рмы в трубах с наличием вихрей на входе.
Г. П. Джордан [72] исследовал теплоотдачу от воздуха в трех медных трубах, образующих калориметры с водяным охлаждением; диаметры этих труб в свету составляли: 12,9; 31,4;
50,0 мм. Среднюю температуру выбирали в интервале от 115 до 300° С, скорость воздуха — от 5 до очень высокого значения — 75,6 м/сек.
Измерение температуры выполняли с помощью ртутного термометра и, по-видимому, термометров - сопротивления перед трубой, охлаждаемой водой и после нее. Следовательно, если даже стенка, охлаждаемая водой, предотвращает или сильно уменьшает влияние излучения на показания термометров, то влияние излучения стенки трубы, омываемой воздухом, полностью сохраняется.
Однако Г. П. Джордан ничего не говорит об изоляции этой стенки, так что точная картина величины ошибки измерения температуры отсутствует. Но неопределенное показание термометра или иного термощупа в потоке газа всегда характеризует слишком малую разность тем/ператур между газом и стенкой, когда безразлично, что горячее — газ или стенка. С повышением температуры эта ошибка будет расти. Так как коэффициент тей- лоотдачи равен количеству тепла, переданному на стенку или от нее, деленному на разность температур, следовательно, при таком методе измерения температуры коэффициент теплоотдачи будет завышенным, прйчем тем сильнее, чем выше температура. Поэтому эта ошибка измерения создает впечатление, что на коэффициент теплоотдачи влияет темпер ату р>а; в действительности этого влияния нет или оно ничтожно. Далее, с увеличением скорости воздуха величина этой ошибки будет уменьшаться. Следовательно, при очень больших скоростях воздуха влияние излучения окружающей среды исчезает вследствие переноса тепла конвекцией. Из этого следует ошибочность показателя степени для скорости в формуле коэффициента теплоотдачи. Однако Г. П. Джордан дополнительно проверял температуры и количества передаваемого тепла на специальной трубе, выполненной в виде калориметра, в котором количество отведенного тепла можно было определить '.путем точного измерения (количества охлаждающей воды и ее температуры. Поэтому такие измерения нужно считать достаточно точными и их можно рекомендовать для практического применения.
В. Нуссельт[73] в своей основной работе исследовал теплоотдачу в латунной трубе диам. 22 мм, которая обогревалась снаружи паром так, что температура ее на всей поверхности стенки оставалась равной 103° и не изменялась с течением времени. Скорости, исследованные им, брались в пределах от 0,6 до 38,7 м/сек, следовательно, охватывали очень широкую область. Температуры воздуха и газа изменялись в пределах от 20 до 77°. При этих условиях Нуссельт, естественно, не мог выявить, каково влияние температуры и диаметра трубы, и основывался в этом вопросе на теории подобия. Надо отметить, что вообще всем измерениям Нуссельта присуща большая точность.
Е. Шульце [74] измерял коэффициенты теплоотдачи от воздуха и дымового газа со средними температурами от 100 до 675° в бесшовных трубах диам. 25, 50, 80, 106 и 150 мм, охлаждаемых водой или воздухом. Несмотря на большие трудности в точном измерении высоких температур воздуха, эти опыты, проведенные в широкой области, имеют большое значение, так как ошибка в измерении температуры была проверена дополнительно.
Температура воздуха на входе и выходе трубы довольно точно измерена Е. Шульце при помощи отсасывающих термопар так, что, если учитывать температуру, измеренную по оси трубы обычными, отградуированными на истинную температуру воздуха термопарами, то такой метод вполне приемлем для получения правильных результатов. Даже очень гладкие и тонкие термопары, установленные в трубе, вызывали, как и в опытах Гребера, возмущения потока. При этих возмущениях коэффициент теплоотдачи увеличивается тем больше, чем меньше диаметр трубы. Поэтому подобная установка термопар может создать лажное впечатление о слишком большом влиянии диаметра на коэффициент теплоотдачи.
Измерения, проведенные фирмой «Бабкок и Вилькокс К°»[75] замечательны тем, что они были основаны на чисто калоримет рическом методе, что в значительной мере исключает температурную ошибку. В опытах применяли смесь отходящего газа с
Воздухом при начальной температуре обоих компонентов до 1200°. Состав смеси: 14,9% С02, 7,9% Н20, 6,8% 02, 70;4% Ы2. Этот газ протекал со скоростями от 4 до 15 м/сек через холоднокатаную медную трубу диам. 50,8 мм и длиной 6,1 му которая снаружи была разделена двадцатью отдельными водяными кожухами на 20 калориметров. Температуру отходящего газа измеряли позади трубы, охлаждаемой водой и вне области излучения охлаждаемых стенок при помощи ртутных термометров. Следовательно, значительной температурной ошибки быть не могло. Температуру газового потока в отдельных калориметрах рассчитывали из измеренного количества тепла. При этом возможность ошибки лежит в пределах точности наших значений удельных теплоемкостей и расхода газа. Эти способы измерения по сравнению с описанными ранее так принципиально новы, что они кажутся нам особенно важными.
Анализ всех без исключения измерений показывает, что результаты 40% опытов не совпадают. Это расхождение результатов наблюдается как в опытах отдельных исследователей, так и при сопоставлении их друг с другом, причем причины этих разбросов и расхождений не указаны. Очевидно, с одной стороны это объясняется неустойчивостью теплоотдачи, а с другой — неизбежностью ошибок в измерениях. Это можно сравнить с положением, когда в доме много часов, показывающих различное время, причем неизвестно, какие часы идут правильно. В этом случае можно быть уверенным, что среднеарифметическое значение из показаний всех часов даст наиболее точное время. Это преимущество среднеарифметического значения является причиной проведенного здесь анализа многочисленных измерений.
Влияние скорости. При равных диаметрах трубы и одинаковых свойствах веществ (при равных температурах) коэффициент теплоотдачи
А = С • т* ккал/м2-час-°С, (236)
Где С — постоянная и — скорость газа при нормальных условиях. Для обеих скоростей потока ш01 и ге>о2 по уравнению (236) должны быть справедливы соотношения
(237)
«а = С • о>ов. (237а)
Деля и логарифмируя уравнения (237) и (237а), получим для показателя степени при скорости соотношение:
Оценивая результаты опытов отдельных исследователей по уравнению (238), получим значения показателей степени для скорости, которые даны в табл. 5.
|
Таблица 5 Показатель степени для скорости
|
Если из всех рассмотренных выше измерений взять по чёты - ре-шесть пар значений, то по показателям степени можно выяснить, в каких случаях температуры были примерно равными, а скорости характеризовались достаточно широкой областью изменения. Это необходимо для получения достаточной точности измерения. Насколько позволяло равенство температур, Шульце ооставил группы равных скоростей с последующей подстановкой их в уравнение (238). Хотя Шульце при пересчете для большинства своих измерений получил равенство скоростей при степени, не совсем соответствующей 0,8, составленные им группы результатов измерений все же пригодны для наших целей, так как ири пересчете вследствие равенства скоростей получается лишь небольшая ошибка второго порядка. В исследованиях фирмы «Бабкок и Вилькокс К°» в основу были положены кривые, отражающие общие результаты (см. рис. 14).
Из табл. 5 следует, что из-за неустойчивых условий при теплоотдаче совершенно точного и постоянного показателя степени для скорости не существует. Однако видно, что показатель степени 0,8, многократно указывающийся как окончательно правильный. является завышенным. Среднее значение из всех показателей степени, согласно табл. 5, равно 0,752, что совпадает с величиной, указанной В. Нуссельтом [76]. Из табл. 5 также следует, что поскольку систематической ошибки в измерении нет, показатель степени для скорости будет уменьшаться с увеличением диаметра трубы. Это подтверждается измерениями как Джордана, так и Шульце. Кроме того, согласно результатам измерений фирмы «Бабкок и Вилькокс К°», показатель растет с увеличением температуры. Несмотря на эту, возможно, реальную зависимость показателя степени для скорости от диаметра трубы и температуры, в дальнейшем, учитывая сильный разброс всех результатов измерений, необходимо подставлять наиболее приемлемое значение показателя
П = 0,75 = const. (239)
Влияние диаметра трубы. По уравнениям (236) и (239) коэффициент теплоотдачи
А = С • w°0'75 ккал/м2*час*°С. (240)
Как известно, коэффициент теплоотдачи уменьшается с увеличением диаметра. Если это влияние диаметра представить снова в виде степени, т. е. через dmt то эта величина, сЛедова-. тельно, должна стоять в знаменателе. Тогда уравнение (240) преобразуется следующим образом:
Ш°’75
Ос == С'--------- ккал/м2*час-°С, (241)
Dm
»
Где С' — новая постоянная.
Для двух диаметров по уравнению (241) справедливы соот-. ношения:
Ш°-75
Ах = С'------ 5---- ккал/м2'Час-°С, (242)
Ш°-75
Аг = С'------ !---- ккал/мг'Час-°С. (242а)
*2
Деля и логарифмируя уравнения (242) и (242а), получим для показателя степени при диаметре следующее соотношение:
|
Т |
![]() (243)
(243)
Влияние диаметра трубы было исследовано лишь указанными здесь исследователями: Г. П. Джорданом и Е. Шульце. Джордан исследовал гладкие медные трубы без вытесняющих вставок диаметром в свету 12,9, 31,4 и 50 мм. Шульце исследовал стальные бесшовные трубы с диаметром в свету 25, 50, 80, 106 и 150 мм. Если оценить результаты измерений обоих исследователей по уравнение (243), то получим различные значения показателей степени при диаметре, приведенные в табл. 6.
|
Таблица б Показатель степени при диаметре
|
|
Г. П. Джордан........................................... |
12,9/31,4 |
0—0,30 |
0,09 |
|
» ................................................... |
12,9/50 |
0—0,26 |
0,12 |
|
» . . . ............................................. |
31.4/50 |
0—0,53 |
0,17 |
|
Е. Шульце.................................................. |
25/50 |
0,4-0,7 |
0,51 |
|
» ....................................................... |
50/106 |
0-0,1 |
0,05 |
|
» ....................................................... |
25/80 |
0,3—0,4 |
0/38 |
|
» ....................................................... |
50/150 |
0,22-0,26 |
0,24 |
|
» ....................................................... |
80/150 |
0,19—0,36 |
0,27 |
|
» ....................................................... |
106/150 |
0,6—0,8 |
0,73 |
|
Среднее значение.... |
0,28 |
Как видно из табл. 6, разброс здесь также значителен. Натянутая по оси трубы термопара в опытах Шульце возмущала поток, как выше уже объяснялось, тем сильнее, чем меньше диаметр трубы. Вследствие этого его измерения дали завышенные показатели степени при диаметре, поэтому необходимо пользо-
10 А. Шак
В. аться не указанным средним значением т=0,28, а более низкой величиной
|
(244) |
![]() M = 0,25 = const.
M = 0,25 = const.
Следует заметить, что эта величина, определенная из многочисленных исследований как средняя, соответствует требованию теории теплового подобия, так как
|
(245) |
![]() Ш ті — 0,2о 0,75 — 1,0.
Ш ті — 0,2о 0,75 — 1,0.
Все измерения проведены без успокоительного участка (или с возмущениями, вызванными введением в поток термопар), вследствие чего наблюдается нормальная турбулентность на входе. Принимая во внимание нестабилизированность теплоотдачи, для упрощения в формулу не введен показатель, характеризующий влияние длины, определенный Нуссельтом выше как функция (L/d)0'05 ; эта величина учтена в постоянной С'. Поэтому необходимо обратить внимание на то, что коэффициенты теплоотдачи в начале трубы (на входе) больше, а в конце трубы меньше по сравнению с средним коэффициентом теплоотдачи, получаемым по выведенным здесь формулам. В случае очень короткой трубы коэффициент теплоотдачи вследствие образования вихрей на входе имеет более высокое значение, чем в трубе нор* мальной длины, равной, например, 100 диаметрам. Если средний коэффициент теплоотдачи трубы длиной 100 диаметров принять равным а, то в трубе длиной 10 диаметров с учетом
(L/d)0,05он равен 1,12 a, a при длине трубы в 2 диаметра —
1,22 а.
В последних работах было установлено значительно большее влияние длины трубы, учитываемое функцией (Ь/с1) 0,13 (см. стр.,466 и далее).
Влияние температуры. По уравнениям (214) и (244) коэффициент теплоотдачи
Шп’
|
(246) |
![]() А — С'---------- ккал/м2’Час-°С.
А — С'---------- ккал/м2’Час-°С.
D0,25
![]() Если бы температура не влияла на коэффициент теплоотдачи, то по уравнению (246) должно было бы
Если бы температура не влияла на коэффициент теплоотдачи, то по уравнению (246) должно было бы
(247)
С' — величина постоянная для всех диаметров, скоростей и температур. Но сравнение с результатами измерений показывает, что величина С' ни в коем случае не остается постоянной.
Чтобы из этих величин выделить влияние температуры, при оценке необходимо учесть, что влияние скорости изменяется и может отличаться от принятого значения 0,75. Вследствие этого значения С' сравнимы только в том случае, когда значения скоростей близки друг к другу. На рис. 17 в качестве примера даны значения С' по результатам измерений Гребера. Обнаруживается явный их рост с повышением температуры. Еще сильнее этот рост наблюдается в результатах измерений Джордана и не-
|
 6 5
6 5
2 7
О 50 100 150 200 250 300 350
Температура воздуха. °С Рис. 17. Измерения Г. Гребера:
О — W0 *= 2,5 до 6 м! сек ф — W% = 7 до 14 мсйк
Сколько меньше (до полного исчезновения) — у Шульце. Следовательно, постоянная С' зависит от температуры. Эта зависимость выражается уравнением
TOC o "1-5" h z С = а + Ъ. fBI (248)
Где а и b — постоянные; tB— средняя температура воздуха. Для обеих температур tBi и tBi по уравнению (248) справедливо
С = a + b-tBl; (249)
С2 ~ я Ь • tB2. (249а)
Из этих двух уравнений следует, что
С —С'9
Ь= , ' . 2 • (250)
*В1 *В2
Коэффициент Ь выражает зависимость коэффициента теплоотдачи от температуры. На рис. 17 он равен тангенсу угла наклона прямой, соединяющей значения С', найденные по результатам измерений Гребера. В этом случае 6=0,002.
Если рассчитать b по уравнению (250) для различных температур при условии наибольшего постоянства скоростей, то получаются средние значения коэффициента Ь, которые даны в табл. 7.
10*
|
Таблица 7 Средние значения коэффициента Ь по результатам некоторых измерений
|
В значениях, полученных на основании результатов исследований фирмы «Бабкок и Вилькокс К°», необходимо выделить влияние излучения углекислого газа и водяных паров, что в настоящее время стало возможным благодаря новейшим данным [77]. Значения Джордана, вследствие их ненадежности, лучше не использовать, так как Джордан, как уже объяснялось, не предусматривал внесение поправки при измерении температуры воздуха. Такое измерение вследствие роста ошибки измерения с повышением температуры дает завышенный коэффициент теплоотдачи; таким образом, влияние температуры, по данным Джордана, будет завышенным. Поэтому в табл. 7 удельный вес его измерений при определении среднего значения коэффициента Ь уменьшен, и, несмотря на проведение им трех опытов, его измерения в качестве среднего значения приводятся всего один раз. Для остальных отдельных измерений Джордана получаются следующие средние значения Ь:
А ъ
11,9 0,0065
31,4 0,0045
50 0,0047
Учитывая приведенные выше рассуждения, в качестве среднего значения примем
Ь = 0,00168 = сопб^ (251)
Тогда по уравнениям (248) и (231)
А = С' —0,00168 . /в. (252)
В постоянную а вошли не только все ошибки измерения, но и ошибки расчета по формулам. Ее отклонение от среднего значения дает степень точности измерений и расчетных формул. Если при оценке измерений обнаружится, что колебания постоянной а значительны и нельзя недооценивать отклонения друг от друга средних значении отдельных измерений, то все же несомненна склонность коэффициента к колебанию. Поэтому применение среднего значения допустимо. Средние значения отдельных измерений даны в табл. 8.
|
Таблица 8 Средние значения d, вычисленные по результатам некоторых измерений
|
Следовательно, среднее значение
А = 3,55 = const. (253)
На основании этого коэффициент теплоотдачи воздуха в трубах равен
И*-75
|
(254) |
![]() А = I 3,55 + 0,00168/,,} • —— ккал/м?-час<°С
А = I 3,55 + 0,00168/,,} • —— ккал/м?-час<°С
Общая формула для коэффициента теплоотдачи
Если учесть определенное выше влияние диаметра и скорости, то, руководствуясь уравнением (175), получим формулу для определения коэффициента теплоотдачи в случае любых газов и перегретого пара:
Ю0’75
А = С • с? • X1" т • —о°25 - ккал/м2 ■ час • °С. (255)
Здесь
С — для всех газов и перегретого пара является постоянной величиной;
Ср— удельная теплоемкость, ккал/нмг • град;
X— коэффициент теплопроводности газа, ккал/м • час •
• град.
В соответствии с вышеизложенными физическими рассуждениями X необходимо было бы брать при температуре стенки трубы, а ср— при средней температуре газа. Но, принимая во внимание сильный разброс результатов измерений и тот факт, что упомянутыми здесь исследователями не установлено влияние температуры стенки, в дальнейшем необходимо значения как К так и ср брать при средней температуре газа или воздуха. Это дает возможность установить для каждого определенного газа точные формулы совершенно простого вида, для которых нет надобности тратить время на поиски в справочниках значений физических величин, пересчитывать их приблизительно в техническую систему и возводить в степень.
Сравнивая уравнения (254) и (255), получаем для воздуха
С-Ср. Х'-т = 3,55 + 0,00168 •/„. (256)
Правая часть уравнения (256) выражается прямой, левая — кривой. Естественно, эта кривая совершенно пологая и в данной области температур практически должна совпадать с прямой.
В общем, для температур £В1 и £в4 из уравнения (256) полу* чим следующие уравнения:
|
(257) (257а) Получим (258) |
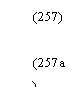 С • с", • X! ~т = 3,55 + 0,00168 • /в1;
С • с", • X! ~т = 3,55 + 0,00168 • /в1;
С • с?2 • 1'2 ~ т = 3,55 + 0,00168 •
Деля и логарифмируя уравнения (257) и (257а), лля показателя степени соотношение:
[ Хх • (3,55 + 0,00168 • и) 1
°е| хг- (3.55 +0,00168 • <вх) ]
|
|
Подставляя в уравнение (258) значения температур /В1 и получим значения показателя т:
*в1= 0; [78]В2 = 300°С; т = 0,823;
*вх = 50; *в2 = 300°С; т = 0,814;
И = 50; /в2>= 200°С; т = 0,812.
Так как по таблицам Юсти * удельная теплоемкость воздуха между 0 и 50 °С имеет аномально высокое значение, то для экстраполяции пригодны температуры выше 50 °С. На основании этого показатель степени для удельной теплоемкости
Т = 0,81
И, как следствие, показатель степени для коэффициента теплопроводности
1 —т = 0,19.
Есл>и эти значения подставить в уравнение (256), то общая постоянная
С= 19,3. (259)
Тогда общая формула для коэффициента теплоотдачи в случае технически шероховатой трубы, не имеющей особого успокоительного участка для всех газов и перегретого пара, запишется в следующем виде:
|
|
|
(260) |
Здесь ср — истинная удельная теплоемкость, ккал/нм* • град и X — коэффициент теплопроводности газа. Обе величины взяты при средней температуре газа в рассматриваемом сечении.
Это уравнение справедливо лишь для турбулентного потока, т. е. для i? e>3000. При ламинарном потоке будут справедливы формулы, выведенные выше.
Достоен внимания тот факт, что показатель 0,81 для ср довольно хорошо отвечает требованиям теории подобия, так как по уравнению (175) показатель т должен бы быть равным показателю степени для скорости, т. е. 0,75. Расхождение можно объяснить точностью измерений в данной области разброса результатов опытов и точностью формул.
Вязкость и коэффициент теплопроводности. В оригинальной работе (см. сноску[79] на стр. 139), показатель т в уравнении (255) определялся с помощью подстановки неправильно взятого значения удельной теплоемкости (0,77 вместо 0,81). Вследствие этого значение постоянной так же изменилось и стало равным 19,3 вместо 20,9. Однако эти изменения формул в числовом отношении оказались незначительными и лежали, особенно при температурах выше 300 °С, в пределах величины погрешности, вызванной недостаточным знанием значений коэффициента теплопроводности.
Чтобы в общем получить необходимые значения X, коэффициенты теплопроводности, измеренные для Нг, N2 и СОг в интервале температур до 300°, а у остальных газов и паров лишь до 100° или еще ниже, Экстраполировались по измеренным значениям на глаз. Но, с другой стороны, коэффициент теплопроводности можно рассчитать из соотношения *
• =-*—, (261)
Где К — коэффициент теплопроводности, ккал/м • час • град;
Cv— удельная теплоемкость, ккал/нм? • град;
П — вязкость, кг • сек/м2;
Е — должно быть, собственно, постоянной величиной. Но она все же изменяется с изменением температуры, а именно, в такой неопределенной форме, что в оригинальной работе пришлось отказаться от этого расчета для уравнения (260). Но так как изменение е, значительно меньше температурного изменения X, которое составляет 100% и больше, то коэффициент теплопроводности все же необходимо рассчитать по уравнению (261).
Для этого наряду с достаточно известной величиной си должна быть известна и вязкость т). Но величина г у большинства газов измерена лишь при температуре до 200—300°, что требует для более широкой области расчета динамической вязкости. Этот расчет ведется по достаточно надежной формуле Сутер - ланда, которая имеет следующий вид:
Т) = —ё. У.Т— кг-се к/м2. (262)
В этой формуле константы В и С определяются по двум измеренным значениям т), затем можно рассчитать вязкость для каждой
температуры. Так, например, для С02 получаем значения В = = 1,65 • 10-7 и С=255. С помощью уравнения (262) получены значения вязкости для важнейших газов, которые указаны в табл. 44 приложения (см. стр. 502). Теперь можно приступить к расчету X по уравнению (261). Значения е, рассчитанные из уравнения (262) для некоторых газов, даны на рис. 18, где штриховыми линиями представлены экстраполированные значения. Видно, что эта экстраполяция еще очень ненадежна; на-
|
А |
'"І |
||||||||
|
-- |
—— |
№. |
|||||||
|
**ч< |
|||||||||
|
"О >( |
— |
||||||||
|
' |
|
$ V* |
|
Температура. °С |
|
О ео ш зоо т 500.600 Температура. °С Рис. 19. Коэффициент теплопроводности азота и водяного пара по измерениям Кейса и Санделла |
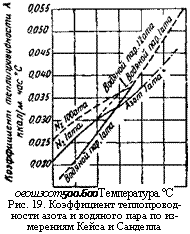 Рис. 18. Величина — в заВИСИМО-
Рис. 18. Величина — в заВИСИМО-
Ся, тг)
Сти от температуры
Пример, у водяного пара имеется налицо всего лишь одна опыт - ная точка измерения. С учетом вероятного хода кривой е экстраполяция проводилась также для азота и углекислого газа. Совершенно неясен ход кривой е, характеризующей водород. Это одинаково справедливо и для не представленных здесь значений е для других газов, в которых измерения проводились даже при 0°С. Несмотря на это, была проделана большая работа по расчету коэффициентов теплопроводности с целью получения хоть каких-нибудь значений, пусть даже неточных и вызывающих возражения. Эти значения даны в табл. 40 на стр. 498. За последнее время наши знания коэффициентов теплопроводности были расширены благодаря проведенным измерениям и экстраполированию.
Здесь необходимо упомянуть измерения коэффициента теплопроводности водяного пара и азота, сделанные Кейесом и Сан-
деллем[80], которые прежде всего ставили своей целью исследовать влияние давления. На рис. 19 даны результаты их работы. Из кривых следует, что коэффициент теплопроводности увеличивается с повышением давления: например, у водяного пара при 300°С в интервале от 1 до 12 ата он увеличивается приблизительно на 6%, а в интервале от 1 до 150 ата — примерно на 75%. Точно так же при увеличении давления с 1 до 100 ата повышает-
Jo
|
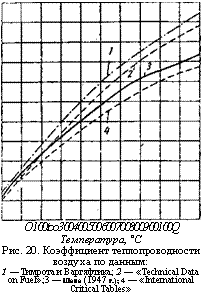
О 100 too 300 400 500 600 700 800 900 100Q Температура, °С Рис. 20. Коэффициент теплопроводности воздуха по данным: 1 — Тимрота и Варгяфтика; 2 — «Technical Data on Fuel»;3 — Шака (1947 г.); 4 — «International Critical Tables» |
 I 0.070
I 0.070
0.065
I 0.060
** 0,055
I
§ 0.050
§ 0.045
% О. ОЧО
%
0.035
I 0,030
% 0.025
10,020
K
Ся значение коэффициента теплопроводности у азота — примерно на 10%- У водяного пара давление оказывает тем меньшее значение, чем выше температура.
На рис. 20 даны коэффициенты теплопроводности для воздуха, взятые из различных источников. Наглядно показаны значительные расхождения (до 25%). Но это не является основанием для того, чтобы отказаться от коэффициентов теплопроводности, вычисленных вышеуказанным методом [81].
Применение формулы теплоотдачи к отдельным газам. Для каждого газа выражение 19,3-с^0*81 Х°-19можно преобразовать в простую температурную функцию, как это уже делали для более узкой температурной области в уравнении (256). В качестве таковых можно выбрать самые различные степенные функции или ряды. В данном случае необходимо отдать предпочтение стандартному выражению
19,3-4>81 • 1°'19 = а + Ы + с?, (263)
Где с может быть равна нулю, если функция описывается прямой.
При температуре 0°С а равна значению 19,3 •^0’81 *Х0’19; Ь и с определяются известным способом из величины 19,3 - с/’81-
•>°',9при наличии двух различных температур, лежащих выше 0°С. Таким образом, для различных газов получаются следующие формулы:
Воздух
А = [з,55 + 0,20 —----------- 0,0066 (—М*
[ 100 100 /
®п’75
|
(264) |
![]() А/л
А/л
Х---------- ккал/м2-час - °С;
А0,25
Углекислый газ (С02)
А = [з,82 + 0,70— -------- 0,033 (—УЧ х
1 100 I 100 /
|
(265) |
![]() Ш°-75
Ш°-75
X--------- ккал/м2-час-°С;
Л>.25
Водород
,0,75
|
(266) (267) (268) |
![]() Г * 1 Щ9
Г * 1 Щ9
А = 5,3 + 0,13--------- —- ----- ккал/м2-час-°С;
[ 100 ] 4°’25
Водяной пар
,0.75
Г * 1 щ
А = 3,8 + 0,26---------- ---------- ккал/м2'час-°С
Коксовальный газ (газ дальней подводки, городской газ)
А = [4,94 + 0,5 —-------- 0,024 (—)*] X
„.0,75
И/л
X--------- ккал/м2-час-°С;
А0,25
SHAPE \* MERGEFORMAT ![]()
|

|
Ккал/м2- час-°С-, |
![]() Метан (СН4)
Метан (СН4)
|
(269) (270) (271) |
![]() А = [4,23+ —---------- 0,019^——)2
А = [4,23+ —---------- 0,019^——)2
I 100 100 /
Этилен (С2Н4)
А = [4,48 + 1,42 -4-------- 0,07 )*] х
I. 100 ЮО / ]
Ш°-75
Х----------- ккал/м2-час-°С;
А0-25
Ацетилен (СгН2)
/ < 21 а>9,'75
4,58 Н---------- 0,055 [------ ) ----------- ккал/м2-час -°С;
Юо юо / ] Гі0*25
Газ при сгорании угля без избытка воздуха (17,6% С02 и 6,5% Н20)
А = [з,60 + 0,26 —------- 0,0076 /——VI х
|
(272) |
![]() I 100 I 100 / ]
I 100 I 100 / ]
Ш«*75
Ккал/м2'Час-°С.
А°-23
(1 — диаметр трубы в свету, м
/ — температура газа, °С.
Коэффициенты теплопроводности смесей газов (коксовальный газ, продукты сгорания) определяются по правилу смешения, хотя этот способ для коэффициентов теплопроводности неточен.
Для каналов с различной формой сечения вместо й подставляют гидравлический диаметр */= —, где / — 'поперечное сечение канала, ж2; и — соответствующая часть периметра канала, через который происходит теплообмен, м.
Вышеприведенные формулы действительны для всех давлений, так как влияние давления учитывается введением скорости №0 (т. е. нормального объема).
Влияние шероховатости поверхности было определено Г, Шефельсом * и Г. Г. Бёмом **. В соответствии с этим коэффициент теплоотдачи, вычисленный по уравнениям (265) — (272), в случае кирпичного канала обычной шероховатости в общем на 25% выше, чем в гладких трубах. В этих работа^ влияние температуры воздуха учитывается множителем |/ Т, что удовлетворительно совпадает с уравнением (254).
Таблица 9
|
Сравнение коэффициентов теплоотдачи различных газов
* Schefels G., Reibungsverluste in gemauerten engen Kanдlen und ihre Bedeutung fьr die Zusammenhдnge zwischen Wдrmeьbergang und Druckverlust in Winderhitzern. Arch. Eisenhьttenw.. 6 (1932/33), S. 477/86. ** Bцhm H. H., Versuche zur Ermittlung der konvektiven Wдrmeьbergangszahlen an gemauerten engen Kanдlen, Arch. Eisenhьttenw., 6 (1932/33), S. 423/31. |
Также важно установить, как отличаются коэффициенты теплоотдачи различных газов по своим числовым [82] значениям. В табл. 9 коэффициент теплоотдачи воздуха при 300°С принят равным единице. Увеличение коэффициента теплоотдачи с повышением температуры отражено в последнем столбце в виде исходной величины коэффициента теплоотдачи соответствующего газа при 0°С.
Вследствие того, что коэффициент теплопроводности при более высоких температурах уменьшается, 'тенденция к увеличению коэффициента теплоотдачи при температурах свыше 300° постепенно затухает.
Во многих случаях можно применять более простую приближенную формулу: для воздуха и продуктов сгорания
Ю°’75
А — 3^8---------- ккал/м2• час • °С. (273)
^0,25
Измерения Эванса и Сарьяна. Недавно вышла в свет работа
С. И. Эванса и Б. И. Сарьяна * по теплоотдаче в трубе от воздуха и дымовых газов, в которой содержатся важные результаты измерения различных величин, например влияния успокоения и возмущения потока. Такие измерения были проведены впервые.
Эта работа имеет большое значение и здесь необходимо дать ее основное содержание.
Была исследована теплоотдача от воздуха в интервале температур до 480°С и от продуктов сгорания городского газа до 870°С в трубах диам. 75 мм и длиной 2,5 м.
Истинная температура газа как в поперечном сечении, так и по длине трубы измерялась при помощи тонкой отсасывающей термопары. Расход определялся по перепаду давления, а распределение скоростей в поперечном сечении с помощью небольшой трубки Пито.
Измерения распространялись почти на все возможные состояния потока: нестабилизированная турбулентность, стабилизированная турбулентность, установка гладких вытесняющих вставок, завихрителей, ламинарный поток.
Стабилизированное турбулентное состояние потока достигалось установкой проволочных решеток в расширяющемся пространстве перед участком измерения и скругленным входом в трубу. Возмущенное турбулентное состояние потока вызывалось установкой винтообразной вставки из жести перед входом.
При установке вытесняющих вставок или завихрителей в трубе было принято во внимание излучение этих поверхностей (вторичные поверхности нагрева), учитывая его при расчете коэффициента теплоотдачи конвекцией уменьшением на соответствующую величину.
Содержание СОг и Н20 в продуктах сгорания менялось путем добавления С02 или Н20 в интервале 15,8—3,8% СОг я 21,5—5,0% Н20. Излучение эти[83] компонентов газа измерялось разностью между измеренной общей теплоотдачей и теплоотдачей конвекцией (воздух) при одинаковых условиях, сравнивая с величинами, полученными Хоттелем и Эджбертрм *.
В этих опытах учитывалось изменение коэффициента теплоотдачи конвекцией вследствие присутствия С02 и Н20, Доля излучения в общей теплоотдаче газа доходила до 25%.
Для коэффициента теплоотдачи при стабилизированном турбулентном состоянии потока оказалось подходящим уравнение (180):
Ъ - Яе0’8. (274)
X
В этом уравнении сг^А — известный безразмерный критерий Нуссельта {N11) и Яе— также безразмерное число Рейнольдса хюйу/цц. Правда, для инженеров, занятых расчетами, использование формул с безразмерными критериями означает лишнюю затрату временц. Но их большое преимущество выявляется в исследовательских работах и заключается в том, что они одинаково пишутся как в английской системе единиц, так и в немецкой технической системе и системе СОБ и имеют одинаковые постоянные, т. е. константа Ь во всех системах единиц постоянна.
Приводимые здесь обозначения:
А— коэффициент теплоотдачи конвекцией, ккал/м2 • час *0С; с1— диаметр трубы в свету, м
Л— коэффициент теплопроводности, ккал/м • час °С;
Ь— постоянная;
Яе— число Рейнольдса (в опыте Яе лежит между 690 и 15100);
Иу0— скорость газа (0°С, 760 мм рт. ст.), м/сек;
То— удельный вес, кг/нмг у]— вязкость, кг • сек/м2 g— ускорение силы тяжести, м/сек2.
Постоянная Ь колеблется между 0,0188 и 0,0222, но большинство значений лежит в интервале от 0,0198 до 0,0208. В качестве средней величины принимаем
Ь = 0,020.
В соответствии с этим формула для коэффициента теплоотдачи конвекцией в трубе при стабилизированном турбулентном состоянии потока запишется следующим образом:
![]() (275)[84]
(275)[84]
В случае нестабилизированного турбулентного состояния потока значения получаются на 30% выше, причем указанная постоянная
Как уже объяснялось, коэффициент теплопроводности определен в опубликованных работах со значительной погрешностью. Автор нашел, что значения коэффициентов теплопроводности, указанные в справочнике «Technical Data on Fuel», отражают наилучшие результаты измерений. На рис. 20 показано изменение коэффициента теплопроводности воздуха в соответствии с этими значениями, пересчитанными в технической системе единиц. Здесь же нанесена кривая изменения коэффициента теплопроводности в зависимости от температуры, построенная автором в 1947 г. на основании вычислений с учетом вязкости и критерия Прандтля. На рисунке указано также изменение коэффициента теплопроводности, по данным «Technical Data on Fuel», и включены также результаты измерений, проведенных русскими исследователями Тимротом и Варгафтиком, ставшие известными автору лишь позднее.
На рис. 21 изображено температурное поле при стабилизированном и возмущенном турбулентном состоянии потока [85] по по
перечному сечению трубы. Видно, что при успокоенном турбулентном движении температурное поле очень сильно изменяется по всей длине трубы, т. е. на длине, соответствующей 33 диаметрам. Но всегда наблюдается случай, когда теплоотдача будет начинаться при входе в трубу.
Особенное значение в этих опытах придавалось установлению оптимального соотношения между теплоотдачей и потерей давления, чтобы, наконец, ответить на вопрос, что выгоднее для увеличения коэффициента теплоотдачи — установка вставки или же гладкая труба с соответственно более высокой скоростью?
|
|
|
Рис. 21. Распределение температур в поперечном сечении потока при стабилизированном (а) и возмущенном (б) турбулентном движении |
|
ТОО 240 280 310 |
|
Те лтература. °С |
|
А |
Доказано, что установка гладких вытесняющих вставок ухудшает теплообмен; винтовая вставка несколько уменьшает коэффициент теплоотдачи, но слегка увеличивает общее количество передаваемого тепла. Разница получается от того, что вследствие увеличения теплопередачи труба может быть короче и поэтому потеря давления во всей установке с одинаковой теплопередачей несколько уменьшается.
В целом же вставки, повышающие теплоотдачу, практически ухудшают соотношение между теплоотдачей и потерей давления. Поэтому вставки рекомендуется устанавливать лишь там, где из конструктивных соображений необходимо применять относительно короткие трубы. К тем же самым результатам задолго до этих опытов пришел и автор (см. главу «Теплоотдача и потеря давления» на стр - 416.
Интересно сравнить формулу, полученную Эвансом и Сарьяиом, с уравнением (264) для воздуха.
Принимая коэффициент теплопроводности, по данным «Technical Data on Fuel» (см. рис. 20), составим табл. 10.
Из табл. 10 следует, что влияние температуры в обеих формулах совпадает, так как расхождения при 300 и 700° практически одинаковы. С увеличением скорости расхождения становятся меньше. Это объясняется тем, что в уравнении (264) скорость стоит в степени 0,75, по данным Эванса и Сарьяна, — в степени
11 А. Шак
|
Таблица 10 Сравнение формулы Эванса и Сарьяна с уравнением (264)
|
ОД С увеличением диаметра расхождения также будут уменьшаться и практически исчезать при диаметрах свыше 70 мм.
Впрочем, константа Ь принята Мак Адамсом равной не 0,02, а 0,0207. С этим значением константы Ь расхождения, указанные в последнем столбце табл. 10, уменьшаются примерно на 3 единицы.
Если же учесть еще, что уравнение (264) дает средний коэффициент теплоотдачи для случая затухающей нестабилизиро - ванной турбулентности, а формула Эванса и Сарьяна, напротив, указывает нижнее значение коэффициента теплоотдачи в случае стабилизированной турбулентности, то моджно говорить о полном совпадении обеих формул, полученных'независимо одна от другой.
Следовательно, для обычной в технике турбулентности потока необходимо, чтобы постоянная Ъ имела несколько более высокое значение: примерно 0,0215. Тогда остается еще ответить на вопрос растет ли коэффициент теплоотдачи пропорционально ®0;75 или до0,8? Но, вероятно, эта степень в еще меньшей меде, чем это указано на стр. 143, зависит от диаметра, так что никакого общепринятого значения для этих степеней не существует.
Сравнивая теперь коэффициенты теплопроводности, данные на рис. 19 и 20, находим, что коэффициент теплопроводности, по данным «Technical Data on Fuel», завышен. Напротив, кривая, характеризующая изменения коэффициента теплопроводности, по данным «International Critical Tables», очень хорошо совпадает с новыми измерениями Кейеса и Санделля, так что в области измерения, т. е. примерно до 400°, эти значения необходимо рассматривать как наиболее вероятные.
Так как новые коэффициенты теплопроводности примерно на. 10% меньше примененных Эвансом и Сарьяном, то, следователь - но, постоянная Ь должна быть в дальнейшем увеличена на 10%, после чего
Ь = 0,0235. (276)
Следовательно, при применении указанных новейших значений. % по Кейесу и Санделлю достигалось бы настолько хорошее совпадение с уравнением (264), насколько это возможно при наличии расходящихся данных по степеням при то. и при - этом для практически всегда существующего нестабилизированного турбулентного движения наличие постоянной 6 =0,0235 будет облегчать решение данной задачи.
На основании всего сказанного можно установить, что уравнение (264) и, следовательно, уравнения (263) и (265) — (272) подтверждены исследованиями Эванса и Сарьяна.
Теплоотдача в начальном участке. В начальном участке, т. е. при не возникшем еще скоростном и температурном поле, коэффициенты теплоотдачи во много раз (на 100% и более) выше, чем в области стабилизированного турбулентного движения. Это явление имеет большое практическое значение вследствие своего влияния на температуру стенки трубы (см. стр. 315), а если говорить в общем, то оно влияет и на величину среднего коэффициента теплоотдачи в трубе или канале, который при не очень длинных трубах, естественно, может быть очень значительным.
Поэтому также важно знать более точно зависимость, по которой коэффициент теплоотдачи уменьшается с увеличением длины трубы (следовательно, с убыстрением возникновения температурного и скоростного полей) и входит в значение, соответствующее бесконечно длинным трубам.
Необходимо еще упомянуть, что знание температуры стенки трубы важно как при высокой, так и при низкой температурах, так как при высокой температуре в стенке возникают напряжения, вследствие образования окалины снижается прочность, а при низкой — на стенке конденсируются водяные пары и серная кислота.
С учетом всего вышесказанного здесь подробно излагаются вопросы теплоотдачи в начальном участке.
К. Эльсер [86] теоретически исследовал теплоотдачу на термическом начальном участке в гидродинамически стабилизированном турбулентном потоке в трубе. При этом речь идет о стабилизированном турбулентном потоке в трубе, температура стенки у которой по всей длине постоянна. Это постоянство температуры стенки цачинйется от определенной точки и от этой точки начинается «термический начальный участок». Изучение этого участка позволяет ознакомиться с начальным участком, часто встречающимся в технике, который отличается от рассматриваемого здесь тем, что на нем не возникает стабилизированной турбулентности, но, проходя по начальному участку, поток изменяется и стремится к стабилизированному турбулентному движению. При этом Эльсер не исследовал характера'потока в начальном участке, на котором не возникает ни скоростное, ни температурное поле, вследствие чего коэффициент теплоотдачи должен иметь более высокое значение по сравнению с получающимися по формулам Эльсера.
Эльсер нашел, что коэффициент теплоотдачи в начальном участке определяется из следующей конечной формулы:
_ |
Nu = 0,183 • Re11'2 • Prmj f-j-'j. (277)
Приведенные здесь критерии аналогичны критериям, указанным на стр. 115. Решая это уравнение относительно а, получим
А = 0,183 • ~~ • ReVl 2 • Pr'/Z (277a)
Из этого уравнения следует, что в начальном участке коэффициент теплоотдачи уменьшается пропорционально корню третьей степени из d/x от самого начала теплопередачи (* = 0). Это уменьшение происходит довольно сильно, так что уже на расстоянии нескольких диаметров от начала возникновения теплопередачи появляется устойчивое состояние.
Напротив, по данным Эванса и Сарьяна, изменение теплопередачи в случае не развитой, следовательно, нестабилизирован - ной турбулентности (образование вихрей на входе) продолжается на более длинном участке.
На рис. 22 представлено падение коэффициента теплоотдачи конвекцией непосредственно позади винтообразной вставки - Коэффициент теплоотдачи на рассто5йши примерно 14 диаметров уменьшается на 2/з своего первоначального значения при наличии высоких скоростей и на Уг при более низкой скорости. Затем коэффициент теплоотдачи принимает постоянное значение, соответствующее стабилизированному турбулентному состоянию потока.
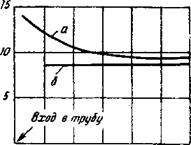
На рис. 23 нанесена расчетная кривая среднего коэффициента теплоотдачи npit возмущенном и стабилизированном турбулентном состоянии потока. Сообразно с этим средний коэффициент теплоотдачи на участке длиной 45 диаметров имеет практически постоянное значение, затем примерно на 10% превышает значе
ние коэффициента теплоотдачи при стабилизированном турбулентном состоянии потока. Вследствие влияния первой, сильно возмущенной части потока на его среднюю часть коэффициент теплоотдачи, соответствующий стабилизированному турбулентному состоянию, можно до-
|

|
Расположение Завихрителя |
![]()
|
О 40 80 ПО /80 200 Расстояние х. см |
![]()
|
Рис. 22. Падение коэффициента теплоотдач * после завихрителя |
![]()
|
20 |||® II. & & |
 Стичь лишь на бесконечно длинном участке трубьЪ.
Стичь лишь на бесконечно длинном участке трубьЪ.
Сравнение рис. 22 и 23 показывает, что коэффициент теплоотдачи, представленный на рис. 22, уже на участке длиной 120 см (на рис. 22: 190—70), т. е.
|
4 |
![]()
|
0/23 Длина труды, м |
![]()
|
Рис. 23. Изменение средних коэффициентов теплоотдачи при несггабшшзираван - ном турбулентном потоке: а — нестабилизированный турбулентный поток: б — стабилизированный турбулентный поток |
 16 диаметров позади места. возмущения принимает свое вероятное конечное значение. Напротив, на рис. 21, б изображено состояние, когда на расстоянии 32 диаметров еще не достигается форма стабилизированного турбулентного движения. По сообщению проф. Сарьяна это
16 диаметров позади места. возмущения принимает свое вероятное конечное значение. Напротив, на рис. 21, б изображено состояние, когда на расстоянии 32 диаметров еще не достигается форма стабилизированного турбулентного движения. По сообщению проф. Сарьяна это
|
Й И |
![]() Можно объяснить тем, что, несмотря на искусственную турбулентность, уже на расстоянии 16 диаметров образуется тонкий пограничный слой, который соответственно определяет теплоотдачу. Необходимо изучить эту проблему еще точнее.
Можно объяснить тем, что, несмотря на искусственную турбулентность, уже на расстоянии 16 диаметров образуется тонкий пограничный слой, который соответственно определяет теплоотдачу. Необходимо изучить эту проблему еще точнее.
Обе кривые на рис. 22 показывают, что уменьшение коэффициента теплоотдачи, взятое в процентах к его первоначальному значению, тем больше, чем меньше скорость. Например, при скорости 10 м/сек (0°С, 760 мм рт. ст.) коэффициент теплоотдачи уменьшался с 14,5 до 7,2, т. е. на половину, а при скорости 16 м/сек — от 16,5 до 10,5, следовательно, лишь на 64%. Из этого следует, что формулы, применяемые до сих пор для расчета падения коэффициента теплоотдачи (а пропорционален Ь/й), вероятно, неправильны и должны быть дополнены фактором, учитывающим скорость. В соответствии с этим влияние данного источника возмущений тем сильнее, чем меньше скорость.
По данным Эльсера (неопубликованное сообщение), при входе в трубу сначала возникает возмущенный ламинарный поток, который лишь на расстоянии около 15 диаметров переходит в (неразвитый) турбулентный. И лишь на расстоянии около 50 диаметров турбулентный поток развивается полностью (по измерениям Кайе, Кинэна и Мак - Адамса [87]). Получается странная кривая изменения коэффициента теплоотдачи. В плоскости поперечного сечения на входе а равен полуторному и двойному значению коэффициента теплоотдачи, которое устанавливается позднее, когда наблюдается установившееся состояние потока. При прохождении начального участка длиной 10 диаметров коэффициент теплоотдачи уменьшается примерно на седьмую часть своего значения при стабилизированном состоянии, оставаясь на этом уровне на участке длиной примерно 20 диаметров и достигая установившегося значения на расстоянии около 40 диаметров. Это изменение коэффициента теплоотдачи потока было измерено названными исследователями.
К. Эльсер в соответствии с этим указывает, что при входе в трубу сначала устанавливается ламинарный поток, который затем, проходя переходный участок, превращается в стабилизированный турбулентный поток. Эльсер рассчитал теплоотдачу на этом ламинарном начальном участке и нашел, что
А = 0,289 • - у • Не112 ■ Ргх/3 ккал/м*-час • °С. (278)
Здесь
Ь— расстояние от входа в трубу, м;
А — диаметр трубы в свету, м;
Яе и Рг — известные критерии (см. стр. 115).
Совершенно иное изменение коэффициента теплоотдачи в начальном участке по сравнению с данными Эльсера и Кайе, 'Кинэна и Мак Адамса, нашли Н. Г. Адамс, У. Е. Кеннель и 1^. Н. Аддомс [88] в опытах с паром. Они получили уменьшение коэффициента теплоотдачи на участке от входного поперечного сечения до места, где наблюдается стабилизированное состояние, пропорциональное (Ь1с1)~0-13,
/ А �-13
“ = <*1(7-) • (279)
Это уменьшение шло на расстоянии до 80 диаметров. В уточненной формуле упомянутые исследователи считают уменьшение коэффициента теплоотдачи в начальном участке пропорциональным выражению (1 + 2,3 - j - ); следовательно,
А = ао ( 1 + ' <28°)
В этих формулах L является расстоянием от места измерения до входного сечения, выражаемым в диаметрах трубы или з метрах. В уравнении (279) ai представляет собой коэффициент теплоотдачи во входном сечении, ао в уравнении (280) — коэффициент теплоотдачи при стабилизированном турбулентном состоянии потока. Уравнение (280) в данной математической форме справедливо, как и все степенные функции, так как оно при большой длине трубы тождественно с ао, который соответствует установившемуся состоянию потока при стабилизированной турбулентности. Но уравнения (279) и (280) не описывают наличия указанного выше, крайне сильного минимума коэффициента теплоотдачи на участке L длиной от 5 до 25 диаметров. Следовательно, это неожиданное появление минимума в значении коэффициента теплоотдачи на начальном участке необходимо изучить более тщательно.
По формуле 1 +2,3 — значение а, взятое на расстоянии
10 диаметров от входного сечения, на 23% выше коэффициента теплоотдачи при стабилизированном состоянии (L = oo) и даже на расстоянии 40 диаметров это превышение составляет 6%. Формула (L/d)0-13 дает уменьшение a на 74% первоначальной величины на расстоянии 10 диаметров.
Еще большее влияние образующихся при входе вихрей обнаружил Поензген в своих опытах по теплоотдаче от водяного пара [89].
По его измерениям состояние стабилизированной турбулентности появляется лишь после прохождения начального участка длиной
L = 2,65 + 8,9 • d м. (281)
Измерения проводились на трубах диам. 39,4 и 95,7 мм. Следо - вательно, длина трубы, необходимая для стабилизации потока, в соответствии с формулой (281) не зависит от диаметра.
Коэффициент теплоотдачи a на участке теплообмена, предшествующем постоянному минимальному значению ао, может определяться формулой
/ Т 0,156
А==Я°'(х) ’ (282)
Где а: — расстояние от начала трубы, м Ьм — определяется по уравнению (281).
Интересно отметить, что показатель степени, появляющийся в уравнении (282), практически равен найденному Мак Адамсом, Кеннелем и Аддомсом и определяется выражением
1 + 2,3^.
Вышеприведенные измерения и расчеты дали частично повторяющиеся результаты, так что необходимо было провести дальнейшее обобщающее исследование. Такое исследование частично с новыми измерениями, частично с использованием всех известных на сегодня опытов выполнено в исследовательском институте, Mannesmann — Forshungsinstitute (Duisburg — Hьckingen) Грассом[90] и в лаборатории Nat. Advis. Comm. Aeron Techn., Note No 1451/1948 (Washington). -
Как и следовало ожидать, тип входа сильно влияет на изменение коэффициента теплоотдачи и это позволяет объяснить часть вышеупомянутых противоречий.
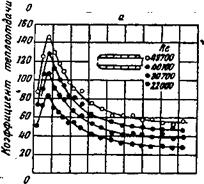
На рис. 24—26 изображены различные формы входа. Если в прошлых работах применялся лишь вход с острой кромкой (рис. 25, а), то в этом исследовании представлены все возможные входные условия.
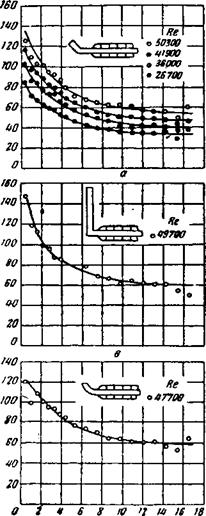
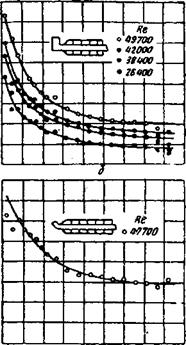
На рис. 27—29 изображено изменение коэффициента теплоотдачи в зависимости от длины трубы (в диаметрах). При этом х — длина трубы в м, считая от входного сечения, и d —диаметр трубы в свету. На рисунках за начало теплопередачи принято начало паровой рубашки, состоящей из отдельных камер. И. Грасс и американские исследователи ставили опыт так, чтобы холодный воздух протекал через трубу, обогреваемую конденсирующимся паром, причем количество конденсата в отдельных камерах паровой рубашки являлось мерой перенесенного тепла. Температуру стенки вследствие очень большого значения коэффициента теплоотдачи для конденсирующего пара принимали практически без ее измерения; с другой стороны, точность определения количества тепла, рассчитываемого по количеству конденсата, можно было контролировать, измеряя тепло, воспринятое воздухом. Все это обеспечивает большую точность данного метода измерения. Расхождение между величиной измеренного
|
Рис. 25. Различные формы входа типа II (*— длина трубы* м) |
|
Рис. 24. Различные формы входа типа I (х — длина трубы, м) |
![]()
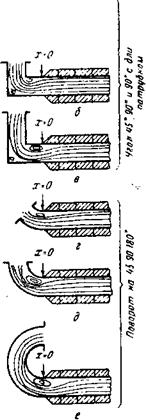 А — острая к ром ка; 6 — свобод ный конец трубы 9 — большой дна метр диафрагмы; г — малый диаметр диафрагмы
А — острая к ром ка; 6 — свобод ный конец трубы 9 — большой дна метр диафрагмы; г — малый диаметр диафрагмы
Х-0
|
Рис. 26. Различные формы входа типа III (х — длина трубы, м): |
А — плавный вход; $ — короткий начальный участок; в длинный начальный участок
|
Коэффициент теплоотдачи ос, ккал/м* час*С |
|
|
|
|
|
|
1 |
О 50 • из |
Т Ш ООО 700 700 |
||||||
|
Г“* |
||||||||
|
•V |
И> 38 ,у» |
|||||||
|
*41 |
"О |
|||||||
|
•т |
||||||||
|
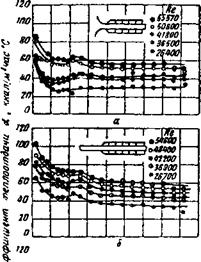
Й 6 8 10 12 11/ 18 18 О 2 * £ 8 10 12 Ш »1$ Расстояние х/О ъ О * Рис. 28. Изменение коэффициента теплоотдачи, вход типа И: х — длина трубы, м; Г> — диаметр трубы в свету, м |
|
Тепла, отданного парам, и теплом, воспринятым воздухом, составляло всегда менее 3%. Прежде чем перейти к выводу формул, необходимо несколько подробнее рассмотреть имеющиеся кривые. Формы входа типа 1 отличаются от рассматриваемого до сих пор острокромочного «стандартного входа» тем, что повороты трубы сделаны частич- Тг |

|
Т 5 юо 80 I €0 А(А |
![]()
|
~г |
||||||||
|
Не • 54800 О 60500 •42000 |
||||||||
|
І, і, э* |
||||||||
|
N |
О 36*00 • 26400 |
|||||||
|
*4 |
В |
|||||||
|
• |
||||||||
|
' |
||||||||
|
— |
Чхядя! |
Яв •28400 •22900 •17000 |
||||||
|
Ь_ |
||||||||
Но под острым углом. Как и следовало ожидать, скругленный роворот на входе, изображенном на рис. 24, е, дает наименьший! коэффициент теплоотдачи на входе и отношение максимального значения к величине коэффициента теплоотдачи, измеренного на расстоянии 17 диаметров, составляет 98:52, следовательно, лежит выше значения ссоо примерно на 90%. Как и ожидалось, сравнение (см. рис. 24, а, б) также показывает, что поворот под прямым углом дает коэффициент теплоотдачи более высокий, чем при 45°, а именно, их значения относятся как 165:133. Во всех случаях коэффициент теплоотдачи на первых 8 диаметрах сильно уменьшается, затем на расстоянии, около 17 диаметров приближается к значению асс. Так как числа Рейнольдса самых
Верхних кривых в случае, изображенном на рис. 24 а, б, а также
24, е, примерно одинаковы, сравнение рис. 24, а и 24, е показы
 Вает, что через 17 диаметров коэффициент теплоотдачи, характеризуемый первой кривой, достигает примерно такого же значения, что и в трубе, показанной на рис. 24, е, с меньшими возмущениями, в то время как сильное возмущение, характеризуемое рис. 24, б (поворот под прямым углом), не успокаивается и после 17 диамет
Вает, что через 17 диаметров коэффициент теплоотдачи, характеризуемый первой кривой, достигает примерно такого же значения, что и в трубе, показанной на рис. 24, е, с меньшими возмущениями, в то время как сильное возмущение, характеризуемое рис. 24, б (поворот под прямым углом), не успокаивается и после 17 диамет
|

|
О 2 4 В 8 Ю 12 Ш!6 18 Расстаони# х/О 9 |
![]() Ров, судя по тому, что а здесь имеет все еще величину 60. Если по рис. 24, б величину «со, соответствующую состоянию стабилизированной турбулентности, вшмем равной 50 ккал/м2 - •час°С, то, следовательно, значение а при входе с поворотом под прямым углом на расстоянии 0,5 диаметров от входа будет равно 185, т. е. 3,3 значения ссоо. Какой является эта величина в начальном входном сечении, на этот вопрос при помощи описанных измерений, естественно, нельзя дать ответа.
Ров, судя по тому, что а здесь имеет все еще величину 60. Если по рис. 24, б величину «со, соответствующую состоянию стабилизированной турбулентности, вшмем равной 50 ккал/м2 - •час°С, то, следовательно, значение а при входе с поворотом под прямым углом на расстоянии 0,5 диаметров от входа будет равно 185, т. е. 3,3 значения ссоо. Какой является эта величина в начальном входном сечении, на этот вопрос при помощи описанных измерений, естественно, нельзя дать ответа.
|
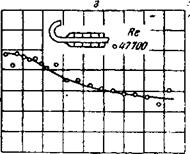
Рис. 29. Изменение коэффициента чеплоотдачи, вход типа III: х — длина трубы, м; О — диаметр тру - в свфгу, м |
![]()
|
Бы |
![]() В формах входа типа II интересен прежде всего вход с острой кромкой (рис. 25, а). Здесь коэффициент теплоотдачи на входе относится к коэффициенту теплоотдачи, взятому на расстоянии 17 диаметров как 132 : 60; следовательно, он в 2,2 раза больше. Так как при форме другого входа (рис. 24,
В формах входа типа II интересен прежде всего вход с острой кромкой (рис. 25, а). Здесь коэффициент теплоотдачи на входе относится к коэффициенту теплоотдачи, взятому на расстоянии 17 диаметров как 132 : 60; следовательно, он в 2,2 раза больше. Так как при форме другого входа (рис. 24,
Б) это отношение равно 165 : 60 (следовательно, больше в 2,75 раза), то из этого следует, что поворот на входе под прямым углом вызывает возмущение потока более сильное, чем простой вход с острой кромкой. Резкое уменьшение коэффициента теплоотдачи в случаях, показанных на рис. 25, а и б^прекращается на расстоянии около 6 диаметров; далее коэффициент теплоотдачи уменьшается медленно.
Минимальное значение коэффициента теплоотдачи на расстоянии 72 диаметров (рис. 25, б, ву г) объясняется, очевидно,
Установившейся возмущенностью в начале трубы, которая действует только на данном участке. Труднее объяснить второй максимум между 4 и 6 диаметрами, в случаях, изображенных на рис. 25 а, б. Можно было бы предположить, что это происходит потому, что ламинарный входной поток по Эльсеру переходит в турбулентный лишь после 4 диаметров, в то время как появлявшиеся ранее высокие коэффициенты теплоотдачи можно объяснить неразвитым температурным полем, т. е. высоким перепадом температур в прилегающих к стенке слоях. Но этому предположению противоречит рассмотрение случаев, показанных на рис. 29, а, в. В случае, изображенном на рис. 29, а, можно со всем основанием считать поток на !входе ламинарным.
Но в другом случае (рис - 29, в) поток вследствие длинного начального участка и высокого (53000) числа Рейнольдса после больших возмущений на входе с острой кромкой безусловно турбулентный, точнее, приближается к состоянию стабилизированной турбулентности. В обоих случаях—как в указанном ненарушающем сопловом входе (рис. 26, а), так и при стабилизирован ной турбулентности на входе (рис. 26, в) — коэффициенты теплоотдачи си совпадают почти точно. Из этого следует, что в противоположность взглядам Эльсера поток уже на входе всегда турбулентен и сильное повышение коэффициента теплоотдачи на входе объясняется лишь неразвитым температурным полем. Второй максимум в случаях, показанных на рис. 25 а. б и т. д., по мнению Грасса, объясняется тем, что в этом месте уже образованный пограничный слой вследствие нагревания и соответствующего расширения будет нестабильным.
Что касается влияния скорости на уменьшение а, то в противоположность высказываниям, приведенным на стр. 166, на рис. 27—29 нельзя отчетливо определить, имеет ли скорость сильное влияние на фактор повышения коэффициента теплоотдачи на входе. В некоторых случаях можно, разумеется, наблюдать, что этот фактор, т. е. отношение си:«оо, при малых скоростях (и соответственно при малых числах Рейнольдса) будет более высоким, чем при больших.
![]()
|
Часто применяют формулу Еида |
![]() Конечная формула для коэффициента теплоотдачи на начальном участке и коэффициент теплоотдачи в зависимости от длины трубы. В четвертом издании этой книги было указано, что вместо уравнения типа
Конечная формула для коэффициента теплоотдачи на начальном участке и коэффициент теплоотдачи в зависимости от длины трубы. В четвертом издании этой книги было указано, что вместо уравнения типа
Так как лишь по уравнению (283) с увеличением длины Ь коэффициент теплоотдачи принимает желаемое постоянное значение. Такая форма была окончательно применена американскими исследователями и Грассом. Из анализа уравнения (283), установлено, что его можно применять как для определения местного коэффициента теплоотдачи (на участке, начиная от £ = 0,5 й)> так и для среднего коэффициента теплоотдачи по всей длине трубы Ь. На основании этого для среднего 'коэффициента теплоотдачи аср по длине трубы Ь справедливо уравнение
Аср == • ^1 + | ккал/м2 • час • °С. (284)
В. табл. 11 приводятся значения с и сср для входа различных форм.
Таблица 11
|
Остоянные для входа в трубу различных типов
И для местного коэффициента теплоотдачи А = /1 + ккал/м2 • час • °С. (284а) |
Уравнение (284) дает средний коэффициент теплоотдачи по длине Ь, если —>5. Уравнение (284а) дает господствующий в
Каждом месте трубы местный коэффициент теплоотдачи для всех
Расстояний от входного сечения, если—=0,5.
Й
На этом проблему теплоотдачи на. начальном участке можно считать окончательно решенной[91].
Теплоотдача при пульсирующем потоке. Г. А. Гейвменн и
Н. Н. Нарайян Рао[92] исследовали влияние пульсаций в потоке на коэффициент теплоотдачи. Были исследованы потоки с числами Рейнольдса от 5000 до 35000 с пульсациями частотой от 5 до 33 гц (колебаний в сек.). Коэффициент теплоотдачи при этом повышался максимум на 30%. Но при малых колебаниях происходило уменьшение коэффициента теплоотдачи. Следовательно, ни в коем случае нельзя сказать, что пульсирующий поток всегда вызывает повышение коэффициента теплоотдачи по сравне
Нию с постоянным потоком. [93]
Определение коэффициента теплоотдачи по температурам
Во всех описанных измерениях коэффициента теплоотдачи измеряли увеличение или уменьшение температуры газа и—/2 °С и по этому перепаду определяли количество тепла <3 по уравнению
Ф = V • ср • (/х — /2) ккал/час. (285)
Если У7—обогреваемая поверхность, м2 tCт—средняя температура стенки, °С; и — средняя температура газа, °С, то
«•£•(/г — *ст) = Ф ккал/час (286)
Или
О
А = — -- —- ккал/м2 • час • °С. (286а)
Р • (*г — >ст)
При этом возникает практический вопрос: что понимать под средней температурой газа? Прежде всего—-это средняя температура на рассматриваемой длине; если эта длина невелика, то достаточно определить среднее арифмети*
Ческое значение из начальной и конечной температур *Х~У* . Но при этом
Необходимо учесть, что начальная или конечная температура сама ни в коем случае не однозначна, так как температура по оси потока газа отличается от температуры вблизи стенки, и необходимо условиться, какая из них должна быть принята. Принимаем во внимание три различные температуры: на оси, среднюю по сечению и среднюю температуру среды, протекающей через рассматриваемое сечение. Если в поперечном сечении трубы радиусом Го круга на расстоянии г от оси господствует температура tt то средняя по сечению тем - пература
2 р
*0 =------ ;------- • °С. (287)
Г0•[94] J
О
Нуссельт вел свои расчеты по этой средней температуре. Гребер *, напротив, делал упор на среднюю истинную температуру протекающего вещества с тем условием, что вещество в рассматриваемом месте цолностью перемешивается. Данная температура не совпадает с t Q, рассчитанной по уравнению (287), Тогда при определении «средней температуры жидкости», необходимо обратить внимание на то, что, например, в холодной трубе холодные слои вблизи стенки текут медленнее по сравнению с быстро текущими слоями по оси; поэтому средняя температура жидкости /ср лежит ближе к температурам на оси, чем к средней температуре по сечению. Это становится ясным при рассмотрении крайнего случая, когда слои, прилегающие к стенке, спокойны, и движутся лишь осевые слои. В этом случае /ср отражала бы температуру осевых слоев без учета слоев, прилегающих к стенке. Следовательню, коэффициенты теплоотдачи рекомендуется рассчитывать по средней температуре жидкости /ср» так как она одна является мерой теплосодержания протекающего вещества, которое необходимо знать и которое надо рассчитать с помощью законов теплопередачи. Эта температура вычисляется определенным методом с учетом распределения температур и скоростей в трубе, найденных из опыта [95]. Сообразно с этим средняя температура жидкости
TOC o "1-5" h z 'ср=-|- -^ + Т °С (288>
И средняя температура по сечению
= • Vе - (289>
Разность этих температур
'ср-*0 = 1Г -«А-Ы) °С - (290)
В этих уравнениях:
IА — температура протекающего вещества на оси;
— температура стенки трубы.
Средняя скорость потока была измерена в точке на расстоянии 0,78 г0 от оси. Средняя температура жидкости /ср господствует на окружности, удаленной от оси на 0,750 г0.
Правда, Е. Щульце измерял температуру на оси, но с помощью вышеуказанного уравнения переходил к /ср - Ритчелл измерял непосредственно /ср, так как его контрольный термометр помещался в месте образования вихрей* где весь газовый поток хорошо перемешивался при помощи крыльчатки. Гребер измерял частично среднюю температуру сечения, частично, вследствие вихреобразования, среднюю температуру жидкости tср . По уравнению (290) различие между и /ср невелико.
Теплоотдача в каналах любой формы. Часто теплоносители протекают не в круглых цилиндрах (трубах), а в каналах с сечениями другой формы. Чаще всего форма каналов бывает прямоугольной, кольцевой (т. е. между двумя концентрически расположенными трубами) и в форме пространства между параллельными трубами. В. Нуссельт [96], руководствуясь экспериментальными данными, а Джордан — расчетом, установили, что в сечениях любой формы необходимо вместо диаметра подставлять следующую величину (гидравлический диаметр):
С1^-Ц1м, (291)
Где / — поперечное сечение потока, м и — часть периметра, через которую происходит теплообмен, м. По уравнению (291), например, для круглого сечения, в котором теплообмен происходит через внешнюю трубу диаметром в то время как внутренняя труба й2 служит лишь для дросселирования,
(292)
4тс • с1г
Для прямоугольных каналов (со сторонами а и 6), в которых теплообмен происходит по всему периметру, гидравлический диаметр
Й = 2а_Ь_ ^ (2дз)
А + Ь
Применяя формулы для расчета гидравлического диаметра, исходят из предположения, что скорость потока по всему сечению канала одинакова (причем отказываемся от обычного профиля распределения скоростей). Это не относится к тому случаю, когда, например, у поперечного сечения узкий выход. При таких выходах среда в канале течет, естественно, медленнее.
В ' последнее время высказывались сомнения, к которым также присоединялся Нуссельт: привильно ли предположение, что для расчета гидравлического диаметра необходимо подставлять величину периметра канала, по которому происходит теплообмен?
Автор пришел к выводу, что лучше подставлять полную величину периметра, независимо от того, весь ли он участвует в теплопередаче или нет. Причина в том, что состояние потока и радиальный перепад температур мало влияют на теплопередающие стенки, независимо от того, передают ли тепло противолежащие стенки или нет. Сообразно с этим уравнение (291) в общем справедливо, причем и равно общему периметру потока, и уравнение (292) можно заменить на (291).
Теплоотдача в трубах при ламинарном потоке
В преобладающем большинстве практических случаев встречается турбулентный поток (по вопросу о турбулентном и ламинарном потоке смотри стр. 87). Раньше всех теплоотдачу при ламинарном потоке теоретически исследовал Нуссельт[97]. Он положил в основу известное параболическое распределение скоростей в поперечном сечении трубы и, предположив, что не существует переноса тепла конвекцией от оси к стенке трубы, составил тепловой баланс для участка трубы длиной Ах, на основании чего удалось получить дифференциальное уравнение теплоотдачи при ламинарном потоке. Решение уравнения дало сложную формулу, которая показывает, что коэффициент теплоотдачи сначала сильно уменьшается с увеличением длины трубы, но затем стремится к постоянному минимальному значению, которого он практически достигает после прохождения участка трубы длиной"
Ь = 0,2 —■*—м. (294)
X
Здесь, кроме известных обозначений, введены:
Г0—радиус трубы, м;
Ср — удельная теплоемкость вещества, отнесенная к условиям опыта, ккал/мъ°С; доср— средняя скорость по сечению трубы, отнесенная к условиям опыта.
Если пренебречь температурной зависимостью ср, то справедливо соотношение
Ср = ср — Акал/м3 °С (295)
« ^ при обозначении через ср удельной теплоемкости нормального объема (0°С, 760 мм рт. ст.).
С другой стороны,
TOC o "1-5" h z ®ср= “Чр • м/час. (296)
Согласно уравнениям (295) и (296)
Ср • “’ср — ср • йУ0ср. (297)
На основании этого уравнение (294) примет вид
Сь • а>0 • го
I - 0,2 —------- 2------- (298)
X
Или, если перейти к обычной размерности для скорости, выраженной в м/сек,
I = 720 • Ср ' Щ ' Г” м. (299)
X
Если учитывать температурную зависимость удельной теплоем-4 кости, отнесенной к нормальному объему, то обозначения здесь следующие:
Ср— удельная теплоемкость нормального объема при средней температуре среды по поперечному сечению трубы, ккал/нм3 град-,
Ьи0 — средняя скорость, соответственно при 0° С и 760 мм рт. ст., м/сек-, г0— радиус трубы, ж;
X— коэффициент теплопроводности, ккал/м • час ° С.
Уравнение (299), определяющее длину пути, которой должна пройти среда прежде чем установится амин, будет справедливо в том случае, если во входном сечении наблюдается равномерное распределение температур. Если же, напротив, происходит распределение температуры, соответствующее установившемуся состоянию теплоотдачи [98], то, конечно, около входа немедленно установится амин (пренебрегая образованием возмущений на входе).
Для коэффициента теплоотдачи, устанавливающегося после прохождения начального участка трубы длиной Ь, Нусеельт дает следующую простую формулу:
Амин = 2,576 • — ккал/м2 • час • °С (300)
Или, если относить, как обычно, к диаметру,
А„ин = 5,15 • — ккал/м2 • час • °С. (301)
С?
Следовательно, коэффициент теплоотдачи при ламинарном потоке и установившемся температурном поле не зависит от скорости и обратно пропорционален диаметру канала. Разумеется, перед участком Ь существует определенная зависимость от скорости, а именно: а увеличивается с увеличением т. Как показывает пример, рассчитанный Нуссельтом, в трубе диам. 22 мм средний коэффициент теплоотдачи от воздуха при прохождении первых 0,5 м увеличивается с 5,4 до 6,9, если скорость возрастает от 0 до 3 м/сек. Коэффициент теплоотдачи после прохождения участка Ь = 1,5 уже не зависел от скорости и был - равен амин = = 5,4 ккал/м2' час °С. Правда, свои эксперименты Нуссельт проводил лишь на трубе одного диаметра (22 мм), но измерения выполнял на различных газах и при различных давлениях.
Результаты этих опытов* хорошо совпадают с рассчитанными по уравнению (301) значениями амин.
Как показали новые измерения, формула Нуссельта [уравнение (301)] справедлива в том случае, если нет подъемной силы и возмущений при входе. Но вообще подъемная сила играет существенную роль в этом вопросе. Это следует из измерений Эванса и Сарьяна, результаты которых для различных скоростей даны на рис. 31. В этих случаях по формуле Нуссельта по лучается слишком заниженное значение коэффициента теплоотдачи. Поэтому в практических условиях при ламинарном потоке необходимо применять формулу Кольборна, которая учитывает влияние подъемной*силы критерием Грасгофа.
Эта формула Кольборна для теплоотдачи от газов и жидкостей при ламинарном потоке записывается следующим образом:
TOC o "1-5" h z X / V, • сп 1/3
А = 1,65 - — • (------------ Ф ) ккал/м2 • час • °С, (302)
Б/ X • £ / 4
где У0—количество жидкости или газа, протекающее за час
Через трубу, нм3/час;
СР — удельная теплоемкость среды, ккал/нм3 °С;
Ь—длина трубы, м;
Ф —условное обозначение выражения 14-0,015 бг,/3 , где С/ г—критерий Грасгофа
Сг = У2.
Г5 * ё
В этой формуле:
Р—коэффициент объемного расширения среды, 1/°С;
0—разность температур (среда — стенка), °С;
То—удельный вес в условиях опыта, кг/мг; g—ускорение силы тяжести, м/сек2.
На рис. 30 сравниваются результаты измерений Эванса и Сарьяна с результатами, полученными по формулам Кольборна и Нуссельта. Видно, что результаты, полученные по формулам Кольборна, очень точно совпадают с результатами измерений.
Так как естественная конвекция при ламинарном потоке играет решающую роль (на рис. 31 а вследствие этого увеличивается почти в 2,5 раза), то положение трубы, горизонтальное или вертикальное, должно иметь существенное значение.
Но по измерениям Киршбаума и его сотрудников (см. стр. 233) конвективные потоки появляются также в трубах малого диаметра, расположенных вертикально, а именно в трубе диам. 30 мм при скорости воды 0,1 м/сек. Такая скорость воды соответствует числу Рейнольдса, которое лежит уже значительно выше критического (2300) значения; следовательно, конвективные
потоки всегда существуют также в вертикально расположенных трубах при ламинарном движении. Это означает, что необходимо всегда. применять уравнение (302), которое учитывает эти потоки [99].
|
Рис. 31. Распределение температур в поперечном сечении ламинарного потока |
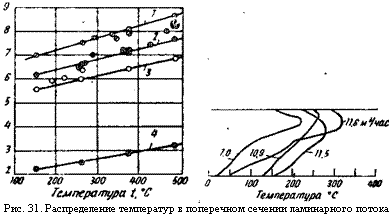 Рис. 30. Сравнение данных, полученных по измерениям Эванса и Сарьяна, с данными, полученными по формулам Кольборна (/, 2, 3) и Нуссельта (4) при различных скоростях ламинарного потока
Рис. 30. Сравнение данных, полученных по измерениям Эванса и Сарьяна, с данными, полученными по формулам Кольборна (/, 2, 3) и Нуссельта (4) при различных скоростях ламинарного потока
Теплоотдача пластин
Вопросы теплоотдачи применительно к пластинам при свободном потоке автор уже рассматривал на стр. 134, опираясь главным образом на исследования Юргеса, Шмидта и Бекманна.
Даже при очень малых скоростях[100] достигается турбулентное состояние потока воздуха. Это можно объяснить в соответствии с числом Рейнольдса большой протяженностью пространства, по которому движется воздух. С увеличением шероховатости поверхности коэффициент теплоотдачи увеличивался на 7% по сравнению с никелированной и полированной поверхностями. В опытах Юргеса была исследована стенка размером 0,5Х0,5 м со средней температурой 51,4°С; она омывалась воздушным потоком, средняя температура которого 20,4°С, подаваемым под давлением 1,05 ата. Основываясь на результатах опытов, Юргес определяет коэффициент теплоотдачи следующими уравнениями:
1) гладкая поверхность аг*ад = 6,122 • ну0,775 + 4,41 • е-0,6ш ккал/м2 • час • °С; (303)
2) окисленная поверхность после прокатки а0Ки„ = 6,137 • да0'780 + 4,60 • е_0'б1В ккал/м2 ■ час • °С; (304) 3) шероховатая. поверхность “шер = 6,649 • да0•784 + 5,03 • е~°-6ш ккал/м2 • час • °С. (305)
|
(306) (307) (308) |
![]() Эти уравнения Юргес заменяет следующими приближенными уравнениями: при скорости ш < 5 м/сек-.
Эти уравнения Юргес заменяет следующими приближенными уравнениями: при скорости ш < 5 м/сек-.
“мая = 4,8 + 3,4 • ха ккал/м2 - час • °С. аокиСл = 5,0 + 3,4 -10 ккал/м2 • час • °С ашеР = 5,3 + 3,6 • ад ккал/м2 • час • °С.
При скорости т > 5 м/сек:
|
(309) (310) (311) |
![]() Аглад — 6,12 • до0,78 «окисл^ 6,14 • ш0,78 аШер = 6,47 • ш0’78
Аглад — 6,12 • до0,78 «окисл^ 6,14 • ш0,78 аШер = 6,47 • ш0’78
В уравнениях (303) — (305) показательные функции е~0, учитывают влияние подъемной силы, которое быстро уменьшается с увеличением скорости хю и поэтому особенно хорошо выражается через функцию е. Юргес под т понимает действительную скорость воздуха, не отнесенную к нормальным условиям. Если же в отдельных случаях температура воздушного потока, омывающего поверхность, лежит значительно выше принятой здесь температуры 20°С, то необходимо напомнить, что по соответствующим результатам измерения т и у одинаково влияют на теплоотдачу. Из этого следует, что при температурах воздуха, отклоняющихся от 20°С, в уравнения (306) — (311) необходимо подставлять скорость воздуха, соответствующую, согласно характеристическому газовому закону, температуре 20°С. При этом, несмотря на изменение удельного веса у, уравнения должны да* вать правильные значения. Если, например, анемометр или иной измерительный прибор при температуре воздуха 60°С показы
вает скорость 5 м/сек, то в предыдущие уравнения необходимо
273 -1- °0
Подставлять значение скорости до = 5 —" - = 4,4 м/сек. Для
273 + 60
Кирпичной стенки и иных технических поверхностей расчет ведут по уравнениям (308) — (311). Если уравнения выведены для вертикальной стенки, то они безусловно применимы также и для горизонтальных стенок, так как вследствие происходящего вынужденного движения влияние подъемной силы отступает на задний план. Кроме того, теплоотдача при свободном движении первоначально спокойного воздуха, судя но сделанным ранее объяснениям (стр. 133—134), не очень сильно зависит от расположения поверхности (горизонтального или вертикального) .
Если пластина расположена в пространстве, ограничивающие поверхности которого характеризуются более низкой температурой, то для определения общей теплоотдачи необходимо к вышеуказанному коэффициенту теплоотдачи конвекцией прибавить еще коэффициент теплоотдачи излучением а „3 (см. рис. 15 и табл. 54). Если же эти поверхности имеют более высокую температуру и °С, то отдача тепла уменьшается на сумму аиз (*1 — 1пл)ккал/м2 • час -° С. В какой мере приведенные уравнения справедливы для более протяженных по сравнению с исследованными поверхностями, еще не выяснено. При оценке этого вопроса необходимо учесть, что температурное поле в воздушном потоке ни в коем случае не соответствовало установившемуся состоянию, которое образовалось бы при значительно протяженных поверхностях, создавая соответствующее скоростное поле при помощи тщательно проведенных мер (удлинение пластины). Следовательно, здесь имеем дело с опытами, которые соответствуют опытам Гребера, где газовый ноток с равномерной по сечению температурой (т. е. с неустановившимся температурным полем) поступает с установившимся нолем скоростей в трубу, воспринимающую тепло. Такое состояние вследствие более высокого радиального перепада температуры у стенки обусловливает более высокий коэффициент теплоотдачи по сравнению с тем, который существовал бы при установившемся температурном поле.
Из этого следует, что в случае протяженных поверхностей будут получаться заниженные по сравнению с рассчитываемыми из уравнений (306) — (311) значения коэффициента теплоотдачи; при этом предполагаем, что воздушный поток не отрывается от поверхности и не образует больших вихрей. В результате эти вихри снова вызывали бы увеличение коэффициента теплоотдачи, как указывалось выше в случае вертикальной пласти - . ны и при наличии свободной конвекции. Если не говорить об очень узких поверхностях, у которых краевые возмущения сильно влияют на коэффициент теплоотдачи, то ширина поверхности вообще на него не влияет.
Интересно сравнить значения, (полученные Юргесом, с коэффициентами теплоотдачи, наблюдаемыми в трубе. При скорости 8 м/сек в трубе диам. 150 мм Шульце нашел значение а = = 25 ккал/м2 • час *°С. По Юргесу же стенка при скорости потока 8 м/сек имела бы коэффициент теплоотдачи а = 6,2 X5,1 = = 31,6 ккал/мчас-°С. Так как стенку можно рассматривать к^к часть трубы бесконечно большого диаметра, которая должна иметь коэффициент теплоотдачи, меньший, чем у трубы диам. 150 мм, то необходимо считать завышенными значения, полученные Юргесом, для больших поверхностей. В опытах Юргеса воздушный поток проходил вдоль пластины высотой 250 мм и шириной 600 мм. Точное измерение распределения скоростей показало, что при различных скоростях невозмущенная скорость потока существовала уже на расстоянии 40 мм от поверхности пластаны. При этом падение скорости было сначала медленным, затем быстрым. Из этого Юргес делает вывод, что воздушный поток двойной толщины, т. е. около 80 лш, был бы достаточным, чтобы играть роль неограниченного воздушного потока. Отсюда можно было бы сделать вывод, что коэффициент теплоотдачи в трубах диаметром свыше 100 мм не должен уменьшаться с увеличением диаметра.
Следовательно, на основе предыдущих рассуждений относительно воздушных потоков, текущих параллельно поверхности длинной стенки, в общем необходимо брать значения коэффициента теплоотдачи, меньшие, чем указано в уравнениях (306) — (311), а именно: тем меньшие, чем длиннее поверхность, омываемая воздушным потоком.
Но практически воздушный поток большей частью направлен к стенке под углом, который лежит между 0° и 90°, что сильно увеличивает /коэффициент теплоотдачи. По наблюдениям Рейера, коэффициент теплоотдачи увеличивается в семь раз, если воздушный поток направлен перпендикулярно к поверхности меньшей длины цо сравнению с тем случаем, когда поток движется с той же самой скоростью параллельно поверхности. При поверхностях с большей протяженностью это повышение ощущается не так сильно, потому что нагретые воздушные потоки отклоняются к поверхности пластины и должны двигаться вдоль нее.
Резюмируя, можно сказать, что в случае плоской поверхности стенки, которая омывается воздушным потоком в неограниченном пространстве, благодаря нормальным составляющим скорости расчет необходимо вести, ориентируясь по меньшей мере на значения Юргеса. При этом необходимо учитывать еще
Коэффициент теплоотдачи излучением аиз, который определяют из рис - 15 (см. числовой пример на стр. 433) [101].
Теплоотдача в трубном пучке
В потоке газа, протекающего «поперек трубного пучка (перекрестный поток), условия движения и теплоотдачи, естественно, совершенно иные, чем при движении в трубе. Впервые теплоотдачу от нагретого до 300° воздуха к одиночной трубе Г. Рейер [102] исследовал в поперечном обтекании для шахматного и коридорного расположения труб. Трубы были длиной 40 см, диам. 4, 6, 10, 15, 18 и 28 мм. Поверхность имела обычную техническую чистоту обработки. В случае одиночных труб скорости составляли 2—6 м/сек, а в случае трубных пучков скорость, измеренная в самом узком сечении в условиях опыта, доходила до
13,4 м/сек. Трубный пучок при этом был помещен в канал шириной 40, высотой 16 и длиной 50 см. Опытную трубу или трубный пучок располагали параллельно стороне канала шириной 40 см и выводили ее концы через стенки канала. Стенки были хорошо изолированы. По трубам протекала холодная вода. Измеряя расход и повышение температуры воды, определяли подводимое-количество тепла. Так как температура трубы всегда была ниже 50°, а температура стенок канала поднималась до 200°, то происходила значительная теплоотдача излучением, определяемая расчетом. Затем величину ее вычитали из замеренной общей теплоотдачи. Это вносило определенную погрешность, так как трубы сделаны из различных материалов, коэффициенты лучеиспускания которых брались из различных источников. Так как гидравлический диаметр поперечного сечения канала был невелик, то нужно предполагать, что поток находился под заметным влиянием стенок канала, особенно его верха и низа, которые находились на расстоянии лишь 16 см друг от друга.
В значительно более широкой области исследовательским отделом фирмы «Бабкок и Вилькокс К0» были проведены измерения, в результате которых, кроме факторов, исследованных Рей - ером, было определено еще и влияние порядка расположения труб. Эти результаты являются исходной точкой последующего изложения.
О. JI. Пирсон [103], положив в основу теорию теплового подобия, исследовал нагревание воздуха, проходящего сквозь трубный пучок, состоящий из десяти рядов по девять труб в каждом. Внешний диаметр труб был равен 7,9 мм и длина 232 мм. Внутри их обогревали электрическим током. Поверхность была гладкой, металлической, потемневшей от нагревания. Температуру трубы устанавливали в интервале 120—400°; температура воздуха на входе составляла 15—25°, на выходе 60—230°С. Было исследовано 38 различных компоновок труб, причем осевые расстояния брались от минимально возможных до трех диаметров. Е. С. Хьюг [104] исследовал теплоотдачу в трубных пучках практически применяющихся размеров. Внешние диаметры труб были равны 12,7; 17,5 и 50,8 мм; длина каждой 1220 мм.
В пучках, составленных из труб диам. 12,7 и 17,5 мм, охлаждение осуществляли водой. Снаружи пучок омывался горячей смесью воздуха с газом, содержащим 1—2% Н20 и 1% СОг - Температура на входе была 315° и на выходе примерно 80°С. Пучок состоял из десяти рядов, в каждом из которых было, по десять труб. А пучок, составленный из труб диам. 50,8 мм, состоял из десяти рядов по девять труб и десяти —!по пятнадцать.
Трубы диам. 50,8 мм изнутри обогревались конденсирующимся паром, подаваемым под давлением около 1,25 ата, а снаружи омывались воздухом комнатной температуры. Все температуры измеряли специальным, точным методом; температуры газа — при помощи отсасывающей термопары. Общая точность измерений контролировалась по отдаваемому количеству тепла, которое, как и у Пирсона, измеряли независимо от подведенного тепла.
В целом было исследовано двенадцать различных компоновок при шахматном и коридорном расположении труб с изменением расстояния между осями от 1,25 до 3 диаметров. Числа Рейнольдса изменялись в интервале от 2000 до 70000. Хотя направление теплового потока, принятое Пирсоном, противоположно направлению, принятому Ниде в его опытах на трубах диам. 12,7 и 17,5 мм, оценка по теории подобия в области, где Яе = 10000—50000, показывает хорошее совпадение их результатов. При Яе = 5000 коэффициент теплоотдачи по Пирсону примерно на 10% меньше значения, данного Ниде. Совпадение результатов служит доказательством того, что коэффициент теплоотдачи не зависит или слабо зависит от направления теплового потока. Е. Д. Гримисон [105]1 использовал результаты обоих вышеупомянутых исследователей, применив теорию подобия, и сравнил их с измерениями других исследователей: Г. Рейера (на результаты измерений и теоретические выводы которого следует обратить особое внимание), Е. Гриффитса и Дж. Г. Оу - берри *2, Т. Линдмарка *3, В. Лориша *4, Е. Л. Чапелля, и
В. Г. Мак Адамса *. Гримисон нашел, что объяснение Рейером температурного перепада между газом и стенкой трубы нуждается в поправке и результаты его измерений рассчитал заново.
Измерения, описанные здесь, очевидно, отличаются значительной точностью. Резюмируя, можно утверждать следующее.
Показатель степени при скорости изменяется как с изменением расположения труб, так и числа Рейнольдса, а именно в пределах от 0,55 до 0,75.
В числе Рейнольдса d означает внешний диаметр трубы, а не гидравлический диаметр свободного пространства между трубами в пучке. В качестве скорости принято ее значение в самом узком поперечном сечении пучка, следовательно, взята максимальная скорость между трубами. В противоположность измерениям Рейера на показатель степени при скорости мало влияет шахматное или коридорное расположение труб. Особенно неожиданным является то, что в абсолютных величинах коэффициентов теплоотдачи при шахматном и коридорном раополо: жении труб с расстояниями между трубами в свету, равными около 1 диаметра, нет существенного различия, как предполагалось до сих пор. При небольших расстояниях между трубами (например, от 0,25 до 0,5 диаметра в направлении потока и несколько больших перпендикулярно ему) шахматноё расположение, напротив, показывает гораздо более высокие значения, особенно при малых числах Рейнольдса (ниже 8000). Так, при Re = = 2000 и межосевом расстоянии в направлении потока 1,5 диаметра и перпендикулярно потоку 2,5 диаметра получается, что коэффициент теплоотдачи при шахматном расположении труб в 1,8 раза больше коэффициента теплоотдачи при коридорном расположении. Напротив, при Re — 8000 и межосевых расстояниях в обоих направлениях 2,5 диаметра коэффициент теплоотдачи при шахматном расположении лишь на 6% выше, чем при кори - Дорном.
* С h а р е 11, E. L. & М с Adams, W. H., Trans. Amer. Soc. mech, Engrs., 48 (1926), p. 1201/28.
Опытное исследование теплоотдачи трубных пучков в зависимости от различных факторов см. дополнительно в работах на русском языке:
Антуфьев В. М. и Белецкий Г. О., Теплопередача и аэродинамическое сопротивление трубчатых поверхностей в поперечном потоке, Маш - гиз, 1948;
Романовский С. А., Исследование теплоотдачи и сопротивления трубных пучков в поперечном потоке вязкой жидкости, диссертация Киевского политехнического ин-та, 1953;
Кузнецов Н. В. и Карасина Э. С., Теплоэнергетика, № 6, 1954;
Исаченко. Ц. П., Теплоэнергетика, № 8, 1955; Сб. «Теплопередача и тепловое моделирование», изд. АН СССР, 1959;
Кузнецов Н. В., Изв. АН СССР, ОТН, в. 5, 1936; Изв. ВТИ № 5, 1947; № 8, 1948;
Тепловой расчет котельных агрегатов. Нормативный метод, ГЭИ, 1957. {Прим. ред.) ]
Число рядов труб сказывается на увеличении коэффициента теплоотдачи только до десятого ряда, а именно: при увеличении от одного до пяти рядов коэффициент теплоотдачи увеличивается от 70% своего максимального значения до 93% и от пяти до десяти рядов — от 93 до 100%. Необходимо отметить, что коэффициент сопротивления каждого ряда («коэффициент трения») одновременно уменьшается от ряда к ряду (примерно со 140% у (первого ряда труб до 100% у десятого ряда).
Все измерения могут быть охвачены следующей конечной формулой, справедливой как для шахматного, так и для коридорного расположения и для пучка с десятью рядами труб:
|
|
В этой формуле:
/р — величина, которая зависит от расположения труб;
X— коэффициент теплопроводности газа при средней температуре между газом и стенкой трубы, ккал/м • час • град т]—вязкость при той же средней температуре, кг. сек/м2;
То—удельный вес нормального объема, кг/м3;
— скорость прохождения единицы объема (при нормальных условиях) в самом узком сечении, м/сек;
(1—диаметр омываемой трубы, м.
Влияние расположения труб
Так как на коэффициент теплоотдачи дополнительно влияют как расстояние между трубами в обоих направлениях, так и число Рейнольдса, то необходимо ввести «фактор расположения» /р. Его значения даны на рис. 32 и 33. В большинстве случаев практическая область чисел Рейнольдса лежит в пределах от 2000 до 8000. Так, для обычных продуктов сгорания или для воздуха, например, при 10о = 3 м/сек, й = 0,03 м и 300°С число Рейнольдса получается примерно равным 4200. Автор выдазил фактор расположения, соответствующий числу Рейнольдса 2000, с помощью интерполяционной формулы - При коридорном расположении труб с достаточной точностью можно записать
![]()
|
(313) |
![]()
![]() /р. к = 1,07-0,65
/р. к = 1,07-0,65
Эта формула справедлива для чисел Рейнольдса, меньших 8000, и для межосевых расстояний, превышающих 15 диаметра,
|
Рис. 32. Фактор расположения /р при коридорном рас* положении труб |
|
Рис. 33. Фактор расположения /р при шахматном расположении труб |
Следовательно, для расстояний в свету больше 0,5 диаметра. Справедливость этого уравнения распространяется примерно до выполнения соотношения
Хю0 . й = 0,2,
Следовательно, большинстве практически существующих условий перекрывается. Сообразно с этим уравнение (312) для пучка с коридорным расположением труб преобразуется следующим образом:
0,0755 — 0,046 ' “ ’
|
А = |
„0.61
»9.01
|
°С. |
![]()
|
(314) |
![]() Ккал/м2 • час
Ккал/м2 • час
^0.39
Или, записывая упрощенно,
|
1.5 “І |
|
.&) |
|
Гм. V 0, 61 ш0 10 |
|
(^) |
|
|||||
|
|
|
|||
|
|||||
|
Здесь |
![]() ~ — межосевое расстояние между трубамй вдоль по-
~ — межосевое расстояние между трубамй вдоль по-
Тока газа, й — диаметр труб [106];
— межосевое расстояние между трубами поперек
Потока газа, й — диаметр труб[107].
С ростом числа Рейнольдса /р в уравнении (312) всегда стремится к единице и при Яе = 20000 становится равным 1, а при дальнейшем увеличении /р в соответствии с выражением в скобках в уравнении (314) приближается к 0,071. Яе =*= 2000 при диаметре трубы 30 мм соответствует примерно скорости
= 14 м/сек.
Из уравнения(314) следует, что при увеличении продольного шага между трубами выражение в скобках, а с ним и значение а сначала очень быстро увеличиваются, чтобы затем, при дости-
-^-=2,5 остаться постоянным. С увеличением с1
Жении значения
|
0,286 |
|
/р. ш = 0,874 + |
|
(іг) |
|
. ^Ро-То |°>61 |
|
X |
|
Ккал/м2 • час • °С. |
|
Й0.39 |
|
0,062 + °’02°- + 0,059 • ' «по 2 Л |
|
Т |
|
Сообразно с этим уравнение (312) для пучка с шахматным расположением труб преобразуется следующим образом: |
|
0,020 № |
|
0,059 |
|
То'61 X |
|
0,062 + |
|
„0,61 |
|
„0.61 |
|
Ккал/м2 • час • °С. |
|
(316) |
|
X |
|
Л),39 |
|
Или упрощенно а |
|
||||
|
||||
|
||||
|
||||
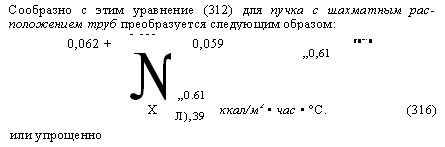 |
||||
|
|
|||
|
Циент теплоотдачи при шахматном расположении на 14% больше; если же установить = 1,5 и =3, то коэффициент
Й г/
Теплоотдачи при коридорном расположении даже на 1 % больше, чем при шахматном. Очевидно, завихрения и большие расстояния при коридорном расположении играют особенно важную роль. Что касается коэффициента теплоотдачи, то он по американским исследованиям в случае коридорного расположения
И при нормальных расстояниях между трубами = 2^
|
Ь То’61 ^.61 |
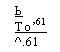 Примерно на 45% больше, чем по измерениям Рейера. При шахматном расположении эта разница составила лишь около 20%. Влияние природы газа. Если попытаться функции
Примерно на 45% больше, чем по измерениям Рейера. При шахматном расположении эта разница составила лишь около 20%. Влияние природы газа. Если попытаться функции
= f(t) (317)
Для отдельных газов выразить, как и при рассмотрении теплоотдачи в трубе, простыми температурными зависимостями, то мы встретимся с определенными трудностями. Так, для водорода значение выражения Х/г] 0,61 при повышении температуры возрастает и соответственно коэффициент теплоотдачи увеличивается пропорционально от 1,23 при 0° до 1,57 при 200°, т. е. на 27%, а при последующем повышении температуры до 300° сохраняет постоянное значение. Такое поведение коэффициента теплоотдачи противоречит результатам проведенных опытов. Кроме того, необходимо учесть, что коэффициент теплопроводности К в уравнении (301) содержится в первой степени. Следовательно, по тем же причинам, что и при расчетах теплоотдачи в трубе (см. стр. 139), удобнее применять вместо вязкости удельную теплоемкость. Переход осуществляется с помощью соотношения (182)
TOC o "1-5" h z —-—= const. (318)
С. Y)
Если найденную из этого уравнения ц подставить в уравнение (301) и учесть, что с — удельная теплоемкость единицы веса, т. е.
С = —ккал/кг • °С, (319)
Yo
То для коэффициента теплоотдачи для всех давлений получаем
Ш0’61
А = с ■ /р • X0’39 • ср,6‘ • —ккал/м2 • час • °С. (320)
Постоянную С нужно определять опытным путем, основываясь на измерениях, которые приводят к уравнению (301), т. е. при
применении воздуха со средней температурой 200°, как и в уело - виях опыта.
Сравнивая уравнения (320) и (312), получим
^0,61 ^0,61
С = 0,071 ----------- — . (321)
■п0[108]61 с0'61
1 ср
Если в уравнение (321) подставить значения физических величин, справедливые для воздуха при 200°, то получим
С == 51,0.
Сообразно с этим коэффициент теплоотдачи при поперечном потоке через шахматный или коридорный трубный пучок будет равен
|
(322) |
![]() Іх = 51,0 • /р • X0,39 . Ср’61-------- ^---- ккал/м2 • час, • °С.
Іх = 51,0 • /р • X0,39 . Ср’61-------- ^---- ккал/м2 • час, • °С.
Р ^0,39
В этом уравнении отражено уменьшение влияния К на коэффициент теплоотдачи и вновь учитывается влияние хорошо известной величины ср. Поэтому становится более возможной экстраполяция.
Функцию X0,39 • Ср61 для различных газов можно выразить с помощью простых температурных зависимостей*, причем, как и прежде, значение функций должно быть таким, чтобы они легко могли быть рассчитаны на логарифмической линейке. Для воздуха,
TOC o "1-5" h z х°.зэ > со. б1 = 0^27у~Т (323)
Или приближенно
Х0.зэ. со. б! = 0 и +_о 009 (324)
100 ;
Функция Л/л0'61 приближенно может быть выражена соотношением
—ПХ-, =*= 72,0 + 3,6 • -±-. (325)
Т]0*61 100
Для максимального значения температуры около 150°, которая была положена в основу в американских работах, изменение коэффициента теплоотдачи составило 12% по уравнению (324) и 9% (по уравнению (325). Разница этих изменений лежит в преде-
Л ах точности измерений. Экспериментируя на воздухе и сильно разбавленными отходящими газами, американские исследователи не смогли сделать выбор между различными формулами теории подобия. Вопреки этому уравнение (322) подтверждается
Опытами так же хорошо, к! к и уравнение (312). Как и при рас
Смотрении теплоотдачи в трубе, в качестве расчетной необходимо выбрать среднюю температуру среды, воспринимающей или отдающей тепло. Следовательно, в уравнении (323) значение Т— есть средняя абсолютная температура воздуха в рассматриваемом поперечном сечении. Значит для коксовального газа
TOC o "1-5" h z X0-39. 61 = 0,012 у'г" (326)
Или приближенно
Х0-39 • с°*61 = 0,21 + 0,025 • — ; (327)
100 '
Для водяного пара
Х°.39 # со. б1 = 0>006 ^/у (328)
или
Х°. 39. со. в1 = о, 10 + 0,016-—(329)
100
Для углекислоты (С02)
TOC o "1-5" h z X0,39 • Ср'61 =а 0,11 + 0,018 • ~~~ I (330)
Для продуктов сгорания угля (теоретическое горение)
X0,39 . с°рЪХ = 0,029 (331)
Или
Х°-39.с°-61 = 0,12+ 0,01-^-; (332)
Для метана (СН4)
|
С°р,61 = 0,13 + 0,027 ; (333) |
![]() ^0,39 „0,61
^0,39 „0,61
Для водорода
Х0> 39 • с°р'61 = 0,035 уТ (334)
V
TOC o "1-5" h z ИЛИ,
X0,39 • Ср"61 — 0,24 + 0,016 • > (335)
Для этилена (С2Н4)
X0,39 • с°р-61 = 0,12 + 0,044 ----- —. (336)
р 100
Важно установить, насколько коэффициенты теплоотдачи при
Одинаковых условиях проведения опытов отличаются один от
Другого вследствие различной физической природы газов. Если
Коэффициент теплоотдачи для воздуха принять равным 1, то
Можно составить табл. 12, где в качестве исходной температуры
|
 Выбрано значение 300°*
Выбрано значение 300°*
|
Рост коэффициента |
||
|
Газ |
Коэффициент |
Теплоотдачи при |
|
Теплоотдачи |
Увеличении |
|
|
При 300° С |
Температуры от 0 до 300° |
|
Таблица 12 |
|
Сравнение коэффициентов теплоотдачи различных газов при поперечном потоке |
|
Воздух...................... Продукты сгорания Водяной пар. . . Водород................... Углекислый газ. . Коксовальный газ. Метан........................ Этилен...................... |
Температурная зависимость для воздуха очень близка к зависимости для дымовых газов, так как удельная теплоемкость О2 увеличивается гораздо больше, чем удельная теплоемкость Ы2. Значительная температурная зависимость этилена позволяет применять этот газ для точного измерения общего температурного влияния на коэффициент теплоотдачи. Сильное отличие водорода от всех других газов позволяет также более точно исследовать коэффициент теплоотдачи этого газа.
Формулы для теплоотдачи различных газов. Подставляя уравнения (326) — (336) в уравнение (322), можно выразить коэффициенты теплоотдачи для" различных газов. Для воздуха при шахматном или коридорном расположении труб
4 л— о'!?'61
А == 1,38 • у Т • fp • —о~з9 - ккал/м2 • час • °С
Или, подставляя /р из уравнения (313) для коридорного расположения труб, получим^
1,48---------- Л-1-
|
Акор |
![]()
|
№ |
„0.61
|
X |
|
Й0.39 |
|
Ккал/м8 • час • °С. |
|
|
Если же подставить /р из уравнения (315) для шахматного расположения труб, получим
,395
|
У ЇХ |
![]() Аш = Гі,205 + —-,395„ + 0,116 •
Аш = Гі,205 + —-,395„ + 0,116 •
|
^о0'61 |
|
А 0,39 |
|
Ккал/м2 • час • °С. |
|
|
||
Аналогично для продуктов сгорания угля (теоретическое горение) :
4 /--- ® *
|
(340) |
![]() А = 1,48 - у Т • /р • —о"з9~" ккал/м2 • час • °С;
А = 1,48 - у Т • /р • —о"з9~" ккал/м2 • час • °С;
|
|
|
Для водяного пара |
|
(341) |
|
Для углекислого газа (С02) |
|
0.61 |
|
^0,39 |
|
Ккал/м2 • час • °С; |
|
А = 5,61+0,92 |
|
100 |
|
|||
Для коксовального газа (газа дальней подводки и городского газа)
|
|
|
|
|
|
|
|
Для водорода
|
|
(344)
Для метана
|
|
|
А = 6,63+ 1,38 . |
|
1C |
Для этилена
( T “-о'61
6,
|
. а == 6,12+2,24 |
![]()
|
(346) |
![]() 12+2,24--- • L —
12+2,24--- • L —
V I00 / d0'39
Фактор расположения /р для шахматной компановки труб можно определить из уравнения (315) или по рис. 33 и для коридорной компановки — из уравнения (313) или по рис. 32. Эти формулы справедливы для всех давлений, так как изменение плотности учтено в выражении через т0.
Теплоотдача одиночной трубы
Измерения Г. Рейера (см. стр. 185), проведенные с применением теории подобия, для теплоотдачи от воздуха, протекающего перпендикулярно к одиночной трубе (находящейся в горизонтальном положении), дали следующую формулу:
|
|
Ккал/м2 • час • °С. (347)
Если, подставив значения физических величин, эту формулу представить в виде простой температурной функции, то для коэффициента теплоотдачи от протекающего воздуха к одиночной трубе получим
Кроме Рейера, опыты по теплоотдаче от воздушного потока к одиночной трубе провел И. А. Хьюгс[109]. Он также применил деревянный канал, но воздух подавал комнатной температуры
и опытную трубу брал длиной 1 м. Труба обогревалась изнутри насыщенным паром давлением 1 ати, а передаваемое количество тепла определялось по количеству образовавшегося конденсата.
Нуссельт [110] обобщил эти опыты с помощью предложенной им теории (рассмотрение подобия) и нашел следующую формулу для определения теплоотдачи конвекцией от газов, движущихся поперечно к трубе:
А = 0,067 • — • (1273 + ±_ЕЩ�,716 ккал/м2 • час • °С.
А т) ; §
Здесь величины Х-у и ц вновь «взяты при средней температуре между газом и поверхностью трубы. Рейер оценил опыты Хьюг - са по своим формулам и пришел к следующему уравнению:
А = 0,326 • — |°’555 ккал/мг • час • °С.
Показатель степени в этой формуле практически совпадает с показателем, найденным Рейером. Напротив, постоянный коэффициент примерно на 10% меньше коэффициента, вытекающего из опытов Рейера. Это объясняется более интенсивным перевешиванием воздуха в опытах Рейера, вызываемым установленной впереди успокоительной [111] решеткой. Поэтому при расчетах в случае не завихренных потоков, пожалуй, лучше применять постоянный коэффициент, найденный Хьюгсом. Сообраз-/ но с этим уравнение (348) примет вид
А = [ 3,6 + 2,7--------- )---------- ккал/м2 • час • °С. (348а)
1000 ) <*0’44
Показатели 0,56 и 0,44 практически совпадают с показателями 0,61 и 0,39, которые справедливы для трубного пучка. В целях сравнения и для более простого пользования формулами, уравнение (348а) необходимо пересчитать на показатели 0,61 и 0,39. Это делается следующим образом. Необходимо, чтобы
Ш0’56 ЙУ0’61
--------- — £ . ------------- .
^0,44 <*0.39
В сущности С должен быть постоянным коэффициентом, но это не всегда так. Однако, если С изменяется не очень сильно, то можно установить некоторое среднее значение.
|
Из предыдущего уравнения |
![]()
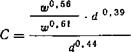 Или, вычисляя
Или, вычисляя
![]() Коэффициент С необходимо вычислить лишь для двух экстремальных и для среднего значений: нижнее экстремальное значение до = 1 м/сек, й = 0,01 м9 С = 1,25; верхнее экстремальное значение до = 10 м/сек, с? = 0,1 м, С = 1,0; среднее значение до = 5 м/сек, (1 = 0,03 м, С = 1,1. Сообразно с этим при С = 1,1 сшибка составляет в общем менее 10% и таким образом уравнение (348а) дает результаты в пределах допустимой погрешности. Затем, как показано выше, при использовании формулы для теплоотдачи в трубе очень трудно точно определить показатели степени и вполне может оказаться, что показатели степени до0,61 и с!0,39 даже правильнее, чем до0,56 и с?0,44. В пользу этого можно было бы сказать, что показатель степени при диаметре 0,44 в сравнении с обычными показателями степени пр# диаметрах кажется достаточно высоким. Следовательно, уравнение (348а) при С = 1,1 преобразуется в окончательную формулу для коэффициента теплоотдачи к одиночной трубе от воздуха, омывающего ее в поперечном направлении:
Коэффициент С необходимо вычислить лишь для двух экстремальных и для среднего значений: нижнее экстремальное значение до = 1 м/сек, й = 0,01 м9 С = 1,25; верхнее экстремальное значение до = 10 м/сек, с? = 0,1 м, С = 1,0; среднее значение до = 5 м/сек, (1 = 0,03 м, С = 1,1. Сообразно с этим при С = 1,1 сшибка составляет в общем менее 10% и таким образом уравнение (348а) дает результаты в пределах допустимой погрешности. Затем, как показано выше, при использовании формулы для теплоотдачи в трубе очень трудно точно определить показатели степени и вполне может оказаться, что показатели степени до0,61 и с!0,39 даже правильнее, чем до0,56 и с?0,44. В пользу этого можно было бы сказать, что показатель степени при диаметре 0,44 в сравнении с обычными показателями степени пр# диаметрах кажется достаточно высоким. Следовательно, уравнение (348а) при С = 1,1 преобразуется в окончательную формулу для коэффициента теплоотдачи к одиночной трубе от воздуха, омывающего ее в поперечном направлении:
Ккал/м2 • час • °С. (349)
Если сравнить эту формулу с уравнением (322), справедливым для трубного пучка, то при факторе расположения [р = 0,72 обнаружим аналогию. Так как /р в%общем лежит между 0,9 и 1*0, то, следовательно, коэффициент теплоотдачи для одиночкой трубы при одинаковой скорости составляет примерно 75% коэффициента теплоотдачи в трубном пучке.
Следовательно, с помощью этого коэффициента /р = 0,72 можно рассчитать теплоотдачу от других газов к одиночной трубе по уравнениям (340) — (346).
Общее уравнение для коэффициента теплоотдачи от газа, протекающего поперечно к одиночной трубе, по уравнению (322) с /р = 0,72 запишется
|
|
Уменьшение теплоотдачи в случае одиночной трубы на 25% по сравнению с теплоотдачей в пучке труб физически объясняется тем, что в пучке труб образуются вихри вследствие обтекания впереди стоящих труб, которые отсутствуют в ^случае одиночной трубы.
Ч0'61
Выражение ——-— представлено графически на рис. 34. d >
С. У. Черчиллем и Дж. К. Бриром [112] исследована теплоотдача к одиночной трубе при высоких температурах (азот от 300 до 1000°С, причем стенку трубы охлаждали до 38°С). Для коэффициента теплоотдачи, осредненного по периметру цилиндра, получается
Nu = 0,60 • Rem. Prm • fZь_°l12. (351)
tctj
Бросается в глаза, что в эту формулу наряду с критерием Прандтля (входит температурная функция, наличие которой, собственно, не допустимо, так как все температурные влияния должны быть отражены в физических величинах числа Рейнольдса
И особенно в критерии Прандтля Ср —— , если используется
^сек
Теория подобия [113].
|
|
Спорость urt м/сек 0)0,61
Рис. 34. Выражение ~т:
FlUi о У
Причина, пожалуй, в том, что для физических величин температура протекающего газа принята Т0 °К, в то время как в действительности правильнее было бы взять среднюю температуру между Г0 и
Значения коэффициентов теплоотдачи, вычисленные по уравнениям (351) и (349), даны в табл. 13.
Таблица 13
|
Теплоотдача к трубе, омываемой в поперечном направлении
|
Данные табл. 13 подтверждают первоначальную интерполяционную формулу, данную автором. Результаты вычислений хорошо совпадают с новыми измерениями, так что нет смысла отказываться от этой простой формулы *.
Теплоотдача при обтекании шара
Для средней теплоотдачи от обогреваемого паром шара, кск торый омывается воздухом, Дж. М. Кэри [115] найдено, что
В точке, где давление струи уравновешено противодавлением,
Следовательно, коэффициент теплоотдачи значительно выше.
Уравнение (352) также можно выразить с помощью более удобной и простой температурной. функции. С погрешностью примерно 3%, которая полностью перекрывается погрешностью,, связанной с незнанием точного значения коэффициента теплопроводности газа, для воздуха, обтекающего шар, получим
Г------- Шл'53
А =? (0,90 + 0,115 у Т ) ккал/м2 ■ час ■ °С. (353)
Здесь Т° К—абсолютная температура воздуха.
Влияние шероховатости трубы. При исследовании одиночной трубы Рейер менял поверхности, во-первых, путем установки на передней стороне трубы ребра толщиной й/Ю и, во-вторых, путем фрезерования 12 продольных канавок шириной 0,2 мм. Кроме того, он исследовал изменение теплоотдачи путем образования сильной турбулентности воздушного потока на гладкой трубе, помещая перед ней трубный пучок. Оказалось, что теплоотдача - после осуществления этих мер сильно увеличивается. Максимальное увеличение оказалось в случае гладкой трубы с турбулизацией воздушного цотока; при небольших скоростях (порядка 2 м]сек) это увеличение составило 47%, а при более высокой скорости (порядка 5 м/£ек) —примерно 55% по сравнению с невозмущенным потоком при тех же скоростях. Установка ребра также усилила влияние скорости. При малых скоростях а - был примерно на 10%, а при высоких скоростях — на 15% выше, чем на гладкой трубе. Наибольший рост показателя степени при скорости наблюдался у трубы, снабженной канавками. В этом случае коэффициент теплоотдачи а при низких скоростях падал даже ниже значения, получаемого на гладкой трубе, а при высоких скоростях а примерно на 30% был выше. Это явление Рейер объяснил тем, что при малых скоростях воздух остается в канавках неподвижным, образуя изолирующий слой. Лишь при более высоких скоростях этот слой исчезает и наступает турбулентное состояние потока, вызванное канавками. Замечательно, что коэффициент теплоотдачи обнаруживает дальнейший рост примерно на 10%, если кромки канавок остались с заусенцами, т. е. если они не были зачищены.
Этот факт подчеркивает, как сильно влияние на теплоотдачу конвекцией незначительных, но резких неровностей поверхности.
Рейер сравнивает свои наблюдения с измерениями Отта, который исследовал теплоотдачу плоских поверхностей с различной шерохо1ватостью. Поверхности были образованы - пакетом динамного железа, в котором тонкие листы чередовались с изолирующими слоями. Это придавало поверхности значительную шероховатость. Хорошо отлакировав эту поверхность, так что она стала гладкой, Отт нашел в соответствии с вышеизложенными результатами, что с увеличением скорости наблюдается значительно более слабый рост коэффициента теплоотдачи гладкой поверхности по сравнению с шероховатой. При скорости,2 м/сек коэффициент теплоотдачи в случае шероховатой поверхности на 25% меньше, а при скорости 20 м/сек на 37% больше, чем коэффициент теплоотдачи в случае гладкой поверхности. При скорости 4 м/сек оба коэффициента теплоотдачи совпадают.
Измерения Юргеса, изложенные на стр. 134, также показали, что с увеличением шероховатости растет и влияние скорости на коэффициент теплоотдачи.
Из рассмотренных «выше измерений можно сделать вывод, что для шероховатой поверхности показатель степени при скорости больше, чем для тлэдкой. При этом коэффициенты теплоотдачи изменяются так, что при малых скоростях а равен или ниже, а при высоких скоростях более чем на 50% выше коэффициента теплоотдачи, чем в случае гладкой поверхности. Таким образом, имеет смысл создавать искусственную шероховатость лишь при высоких скоростях, например выше 4 м/сек. Разумеется, этот предел скорости зависит как от вида шероховатости (чтобы беспрепятственно могли образовываться спокойные слои), так и от вязкости и плотности протекающего вещества (в форме числа Рейнольдса). В соответствии с этим предельная скорость, при которой наступит повышение коэффициента теплоотдачи, вызванное шероховатостью, при удвоенной вязкости по сравнению с воздухом равнялась бы 5 м/секу а при удвоенном удельном весе—1,2 м/сек. Но эта зависимость может быть также иной, чем пропорциональная числу Рейнольдса.

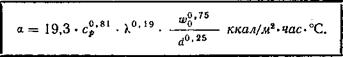
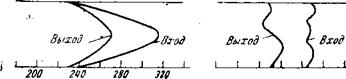
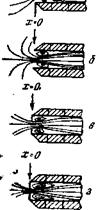
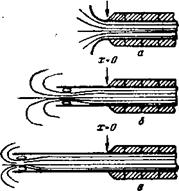
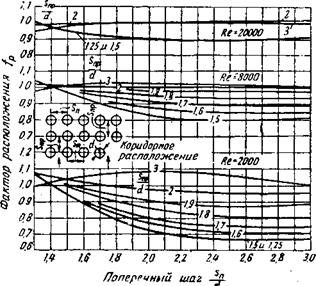
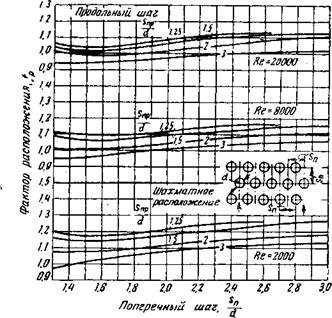

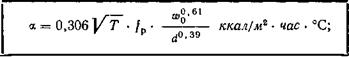
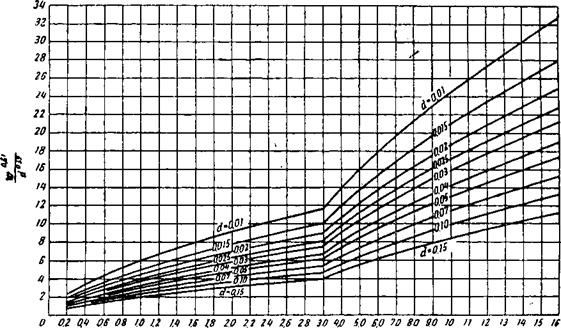
 Опубликовано в
Опубликовано в