ВЛИЯНИЕ ПЕРЕМЕННОЙ температуры газа и воздуха В РЕГЕНЕРАТОРЕ на коэффициент теплопередачи
 3 июня, 2013
3 июня, 2013  admin
admin Опубликованная * ранее автором формула была выведена с некоторыми допущениями, необходимыми в процессе интегрирования. Поэтому эта формула дает правильные результаты лишь в случае регенераторов с равными водяными числами газа и воздуха, что Практически встречается очень редко. Следовательно, для этой важной части знаний по регенераторам необходимо вывести новые формулы.
В газовый период
= “г (8г — 8г. пов) ' иах ' а тг ккал (700)
И соответственно, исходя из свойств кирпича,
(!()г = -- 2~............ 71 аЙг пов ■ и лх ккал. (701)
Здесь, кроме известных обозначений,
И~— пёр*ме? р взываемой поверхности нагрейа, м х — расстояние от входа горячего гэза, м.
Следовательно," Цйх — омываемый элемент поверхности в рассматриваемой точке, удаленной на расстояние а: л« от входа горячих газов. Ниже будем пользоваться обозначением йРх или С1.х — Рх ж2, чтобы иметь возможность охватйть также и регенераторы, поверхность нагрева которых из-за насадки не имеет точно определенного периметра. Приравнивая уравнения (700) и (701) и деля на ^тг. получим равенство
£ ' * ‘ Т ^ ^Г. ПОЙ
----- 2----- • Ч • “ вР (*г - 8г. пов) • (702)
В этом уравнении отсутствует искомое возрастание температуры газа ~—.
Атг
Однако Э1Ч) повышение температуры газа появится, если уравнение (702) еще
Раз продифференцировать по тг. Получил»
TOC o "1-5" h z «•[193]•7-1 «г.«,
2 ' (?03)
Зи,........ с 8 ’" . з.-у, + ±8аа.. (704)
2 • «г
С • 5 - 7 • ТГ) ^ &г. пов
Выражение ——т~--- •--------------------------------------------------------------------- по уравнение (701) $гщ»;не что иное,
- «:г
как количество тепла ц ккал/м2 .шс (удельная теплопередача), передаваемое на 1 м2 рассматриваемого участка х за врем» Яг, равной 1 часу. Следовательно,
С • $ • 7 • 1) пов
TOC o "1-5" h z = ц ккал}м* час (705)
2 4тг у '
«ли после дифференцирования
£ • 8 • 7 * ТЗ „Лв
--------- — •--------- (706)
2 </т^ йтг
С учетом этих уравнений уравнение (704) преобразуется следующим об
Разом:
Й$г 1 2д
-г - Зг---------- • ~г~ +------------- *---- вС/час. (707)
атг аг атг с 8 у г)
Это дифференциальное уравнение в такой форме решить нельзя, так как оно содержит слишком эднрго переменных. Проанализируем данное уравнение. сШ |»
Величина —------ представляет собой повышение температуры газа за 1 час,
Й~г
Ее можно записать также в виде
—, (708)
Сі тг Дхг
А также
<*<7 ?тг-?о
---------- • (709)
И хг ДХр
Здесь:
$го — температура газа на расстоянии х в начальный момент времени, °С;
—температура газа на расстоянии х, спустя Тг часа*, *С;
Яср —удельная теплопередача на расстоянии х за время т/2, ккал/м2- . час (следовательно, среднее значение, предполагая линейный характер изменения температуры);
Яо — удельная теплопередача на расстоянии х в начальный момент времени, ккал/м2 • час
Ях ~Я — удельная теплопередача в точке х, спустя т часа; г
Атг — рассматриваемый отрезок времени, час.
Следовательно, уравнение (707) запишется в виде дифференциального уравнения
»г. хг“»го 1 2-9
------ Е_------ _------------------ ^-------- +---- —- С/час.-------------------- (710)
Атг аг Атг с-5*7-т|
Здесь вместо <7 [уравнение (707)] введено значение <7,?р, так как <7 — производительность поверхности нагрева за время йхт. Если же рассматривать конечный отрезок времени Ат, то вместо ц необходимо подставить среднее за время Ат г значение <7гр. Палее:
СР — средняя величина удельной теплопередачи по всей поверхности
И. х=*Рх за время тг, ккал/м2 . час;
<?0СР - т*то же, для времени О;
Уо — количество греющего газа, нм?/час
Ср «— средняя удельная теплоемкость данного количества газа в области рассматриваемых температур, ккал/нм?. град.
На основании этого из теплового баланса получаем соотношения:
TOC o "1-5" h z рх ' *Чср = ^гО • ср ■ (&п — ахг) ккал/нас; (711)
Рх ■ <7оср = ''го • ср ■ (&гх ~ 8го> “кал/час. (712)
Здесь 0Г1°С—постоянная температура газа на входе. Из уравнений (711) и
(712) следует равенство
Рх (?тгСР - <7оСр) = ^Г0 • ср * (&го - 9г ^ ккал/час. (713)
Но в уравнении (710) дано не среднее значение теплопередгчи по всей поверхности Рх ^2» а значение в точке х. Определив коэффициент теплопередачи, будем иметь
%
TOC o "1-5" h z ср =------------------- (&Г. Ср тг ~ &в СР т.) ккал/м* • час; (714)
Тг. п г *
Чо СР = “ • (9гОСР — авОСр) ккал/м*■ час-, (715)
<7 = -- --------- (8Г — 9В ) ккал/м‘ час; (716)
Г X
Ъг. п
У.
Д0 = —:— . (0Г§—&в0) ккал/м2'час. (717)
тг. п
8 этих уравнениях:
^г. СРтг —средняя температура газа за время тгдля поверхности
Рх омываемой газом;
^в. СРт — средняя температура воздуха за время т для поверхности Рх. омываемой воздухом;
^г. оср и ^в. ос р —то же» Для времени 0 (начало);
$г х —температура газа за время тг в рассматриваемой точке х;
&го — то же, для времени 0;
&Вт и 8В0—соответствующие температуры воздуха;
Тг. л—продолжительность газового периода (половина периода).
Из уравнений (714)—(717) следует
^г. СР тг ^в. СР тв &Г.0 СР ^в. О СР
Чср-*.ср—(7|8>
Теперь с достаточной точностью
8г. СР Т. — ®В. СР Т. 8г. СР 0 ~ 8в.0СР
8Г1г-*в‘в #Г0~°В0
Следовательно, соответствующие температуры изменяются все одинаково. Поэтому будет еще точнее, если вместо обеих частей уравнения (719) подставить среднюю во времени величину
^г. СР ^в. СР
А и
^г. ср в. ср
Тогда уравнение (718) примет вид
СР — ^в СР
9тгср - <70 СР = "Г--------- 1ГГ------ ~ Ч»} ккал/м* час - (720)
' г. ср в. ср
Здесь СР и 9В ср — средние температуры по всей поверхности Т7* за данный отрезок времени; следовательно, &г. ср и &в. ср—средние во времени температуры поверхности с1Рх в точке, удаленной от входа. на расстояние хм. Если выражение дх СР—<?оср из Уравнения (720) подставить в уравнение
(713) и решить его относительно Яхф—Яо» то
V TOC o "1-5" h z - с А _____ 0 ;
„_______ 0 р п а X ГСР ВСР /79П
Ч Чо - рх ('гтг го) 8гСр_»вСр - <7 >
Если же ях —подставить в уравнение (710) и для сокращения и более г
Удобной характеристики повышения температуры газа за время Дтг положим, что
»г, г-»гО = Д»г °С.
То для искомого повышения температуры газа после омывания поверхности получим выражение
|
И |
![]() Л»г =------------------ ;------ ^РАтЛ----------- —--------------- °С. (722)
Л»г =------------------ ;------ ^РАтЛ----------- —--------------- °С. (722)
С.,.т. . . , Гср 8СР
?х ^г. СР ““ &в. СР /
Это уравнение отличается от упомянутого в начале, ранее выведенного уравнения величиной —-Г...ср,<)в-ср— в знамена-
^г. СР ^в. СР
Теле. Она равна 1 лишь для регенераторов, в которых газ и воздух имеют равные водяные числа, т. е. Уот-срГ= Уол'С в.
Определив коэффициент теплопередачи регенератора;—можем найти
Щср 1— • (вг. ср — ®».ср) ккаА’/л^* нос, (723)
Тгл
Подставляя это выражение в уравнение (722), получим уравнение, по которому можно рассчитать повышение температуры газа, омывающего поверхность Fд. м2 в интервале времени 'А*г часа:
|
|
|
(724) |
Коэффициенты х и ц[г относятся р рассматриваемой точке регенератора.
Температуры *г. ср и $в. ср можно рассчитать, исходя из теории теплообменников или соответственно регенераторов. При противотоке [см. уравнение (507)] имеем
TOC o "1-5" h z ' рх ' (~------------------- Ч
&г. ср-»в. ср=(»Н-*э2ср)- е ' °С. (725)
При этом водяное число газа за период
^т-Уто-с г - тг. п ккал/пер °С (726^
И воздуха
УВ = Ув0 - сРв • хв. п ккал/пер-сС. . (727)
&г1—температура газа на входе, °С;
&в2ср — средняя температура воздуха на выходе, °С. Необходимо учесть, что обычно по теории регенераторов расчет ведут по средним во времени температурам; поэтому с самого начала в уравнение (725) была подставлена величина &,..ср вместо . Следовательно, &г. ср— &в. ср является средним значением величины &г<ср— &в. ср по поверхности нагрева Рх.
Таким образом, пользуясь известным способом, по уравнению (725) найдем среднее значение
|
”К. СР1~ |
|
”К. Ср2 |
|
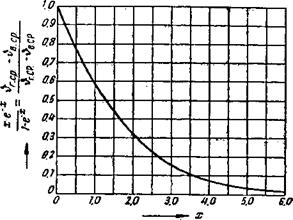
Рис. 59. Отношение средних температур—^^-------- |
|
|||
|
|||
|
|||
|
|||
|
|
||
|
|||
(период газа — <1)
Следовательно, по уравнениям (725) и (729)
|
(*Ч) |
|
Г. СР ' |
|
В. СР |
|
|
|
|
|
|
|
|
|
|
Это выражение зависит лишь от «переменной
1
|
(731) |
И изображается на рис. 59. Однако кривая на рис. 59 рассчита-
№ И7Г
На лишь для случая, когда — < 1. Если —— > 1,
|
|
||
|
|||
|
|||
|
|||
Затели в уравнении (730) будут положительными.
Теперь* известны все величины для расчета повышения температуры газа по уравнению (724) в каждой точке регенератора и для любого отрезка времени 1Лагг.
Для расчета изменения температуры воздуха во времени служат нижеследующие уравнения (обозначения те же, что и для газового периода, но со значком *в>).
TOC o "1-5" h z Л1, = • (»„.„ев — 8„) арх ■ * % ккал> (732)
Л 8в. пов- **Х ккал - (73Э)
Из этих уравнений таким же способом, как и в случае уравнения (704), по
Лучим
CS.-r.-l) ^»в. пов /,й
F------ (734)
rfxB 2аь dx dzb
Следовательно, то же самое уравнение, что и уравнение (704). Но в противоположность уравнению (705)
Cs-t-I dVnoB
Чл------ „ • . • (735)
2 dzB
Отрицательный знак перед------- означает уменьшение температуры ^в-пов*
ИТв
Теперь тем же способом, что и для уравнения (710), получим
|
(736). |
![]() ___________________ 2дв. 1 dqB
___________________ 2дв. 1 dqB
Dz в csi^i ав dzB
Или
|
(737) |
![]() А»в _ 2Уср [ 1
А»в _ 2Уср [ 1
Ахв cs-fr) ав dzB *
Так как Фвв >#вх, то Фвх — 0ВО =— Д0В.
Если і7 лі2 — общая поверхность нагрева регенератора, то при противотоке в точке Fi воздух будет омывать поверхность F—F|. На рис. 60 нанесены кривые, схематически характеризующие изменения температуры.
В случае воздуха для противотока из теплового баланса следует
TOC o "1-5" h z (Р - Fi) ‘ Чв чср = V0B • С#>в (»„ Тв - 9в1); (738)
№ 0 СР == ^0в * срв (^в 0 ^в I) * (739)
Отсюда
(■F “ F1> (Яв О СР Я Т ер) = ^Ов * СРъ ' ^вО х) * (74°)
Уравнения (714)—(717) остаются неизменными, однако для их решения необходимо рассчитать средние значения по поверхности, омываемой воздухом. Следовательно, по уравнению (720)
^г. ср * ^в. СР
Яв твср Яъ о СР = "7 За ’ хв о)* (741)
^г. ср ^в. ср
По методу, примененному к уравнению (722), определяем изменение температуры воздуха после омывания поверхности нагрева ^ — Л м2 за время Дт„ часа:
|
, , ^0всРв^г. ср ^в. ер) 1 |
|||
|
С ‘ $ • ч • Г1 |
^ ав.(ґ-ґ,). |
(^г. СР ~ ^в. Ср] |
|
|
А 9- — |
2х(&г. ср-&в. ср)- |
Дхв |
°С. |
|
1 А О |
А а "г. ср ив. ср |
||
|
- — а^Р-РО |
®г. СР —9в. СР |
|
2 ' ^в. гр Дтв |
|
ИЛИ |
|
(743) |
|
(742) |
![]()
|
Поверхность нагрева Рх, м2 |
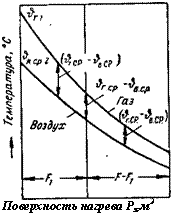 Здесь ■О'г. ср и ■в'в. ср—средние значения температуры газа и воздуха по поверхности, омываемой воздухом.
Здесь ■О'г. ср и ■в'в. ср—средние значения температуры газа и воздуха по поверхности, омываемой воздухом.
Рис. 60. Распределение температуры в противоточном теплообменнике
Из рис. 60 видно, что для расчета средней разности температур по поверхности, омываемой воздухом до рассматриваемой точки 5ь по смыслу в качестве начальной разности температур необходимо подставлять величину ■вр. ср—&„.гр. Если изменяющуюся разность температур между Р х= Р и Рх = Р обозначить через Ог — Ов, то по теории теплообменников, работающих по принципу противотока (см. ниже уравнение 775 на стр. 396), подставляя значения, данные на рис. 50, имеем
и среднее значение разности температур на щоверхности ^ — /м, омываемой воздухом,
Е
У. СР — &«ХР =* Р^_Р1 ' ■ (вг. ср—»в. ср) х
Р,
TOC o "1-5" h z - к • 1РХ-Р,) ■ (—---- Ц
Хе ^ (1РХ (745)
»,ср - »«р - ' *г-,-7|,Я’ , ■ X
^("57 “'п)
Х\-е г »>}■ (746)
Следовательно, искомое соотношение разностей температур в воздушный период равно
/ Уср ~ Уср _ ^ ^ (№у Ц7„) (747)
V 8Г. СР — 8В. СР / _ж . (/г_/г,) ./_!------------------------ !_
Функция ---------------- , где
1 —е~х
* = *. (/=■ _/?х). V
Уг Ув)
Дана на рис. 61. Здесь ^ м2 — общая поверхность нагрева и Т7 —
— Т7! — поверхность нагрева, омываемая воздухом до рассматриваемой точки. Однако кривая на рис. 61 рассчитана лишь для
^ 1 случая, когда —51 < 1 . Если же — > 1, то выражение
№ в У* г Гг
—— будет отрицательным, вследствие чего показатель в уравнении (747) будет положительным.
Если регенератор работает по принципу прямотока, то в газовый период получаются такие же соотношения, как и при противотоке, следовательцо, повышение температуры газа при прямотоке в соответствии с уравнением (724) будет равно
Но в этом уравнении разности температур ^г. Ср“~ ^в «'р и &г СР — &вСР имеют иное значение по сравнению с противотоком. По теории теплообменников [уравнение (531), стр. 322] при прямотоке переменная разность температур
—
|
|||||
|
|||||
|
|
|
|||
Здесь опять подставлены средние во времени температуры ^г. ср и
'вер •
|
Е. о |
|
|
15 10 |
|
О ал ко м го и ю м «о аь 5.0 56 ьо ~ - X |
|
ФГ Т'Р (период дутья — <1) № в? |
|
|
Йц,^р1-------- ^К. Ср2 Рис. 61. Соотношение оредних температур—^—— |
 |
Усредненная в данной точке разность средних по времени температур »получается из уравнения (749)
Рх р 1_Л
|
Г. СР в. СР" |
![]() Ір,; (750)
Ір,; (750)
После интегрирования
|
|
||
|
|||
|
|||
|
|||
|
|||
Следовательно, по уравнениям (749) и (750)
|
^г. гр ^в. ср ®г. СР — 9в. СР |
![]() %’р*' (-^— + -4-) X
%’р*' (-^— + -4-) X
TOC o "1-5" h z »'г /
Г(— +—)
Ч гг ув )
Х---- £------------------------- . (752)
—% рх + _
1 _е V *г *в)
Это выражение является одинаковым по форме с уравнением (730) и отличается лишь переменной:
Нг+^г)- <753>
Значение этой (переменной определяется по рис. 61.
Для расчета изменения температуры воздуха справедливы те же уравнения, что и для газа, так как воздух омывает ту же поверхность Рх ж2, что и газ. Следовательно, изменение температур воздуха при прямотоке после омывания поверхности Р х равно
*(*%. ср ^В. Ср) Д тв_____
^ в о * ср. В ' (^Г. гр ^в.
В. прям
V п • * • 5 • 7 • Ч
^г-сР ^в-ср
|
1 |
![]()
|
^У'Чг. СР ^в. ср) |
![]() СрЛ ’
СрЛ ’
Величину ----- - сР ав‘ср - определим из уравнения (752) или
^г. СР ~ ^в. СР
По рис. 61.
Некоторые замечания к вопросу изменения температуры газа и воздуха. Результаты, рассчитанные по уравнениям (724) и (743), очень хорошо совпадают с результатами современных измерений. При исследовании работы каупера, проведенном Г. Нойманном, А. Шаком, П. Кюном и В - Франценом *, получились следующие результаты:
На стороне отходящего газа ёыло
Х = 6,0 ккал/м2 • пер • °С в = 0,05 м
&г. ср-&в. ср = 70°С т= 1850 кг/*»;
&г. ср-&в. ср= 170 °С т) = 0,95;
У0 = 5500нм3/час с • в • 7 • т) = 18,5 ккал/м2- °С;
Ср. == 0,36ккал/нм3 • °С аг = 6,2ккал/м2-час°С;
Тг - п — 2 часа Рх = /■ = 6450 л2;
___________________ ст = 0,21 ккал/кг ■ °С.
* ММ, Уагте51е11е, УЛХЕИ., №. 82 (1926).
Если эти значения подставить в уравнение (724), то увеличение температуры отходящего газа за 1 час будет равно
МГ = 22,2°С.
По результатам измерений эта величина 22° С (см. рис. 13 названной работы).
На стороне горячего воздуха х = 10 ккал/м2 ■ пер > °С
5 = 0,05 м
&т ср—&в ср = 300 °С с = 0,25 ккал/кг • °С;
Ав = 8,5 ккал/м2 • час • °С у — 1850 кг/м3;
Ув0 = 15 000 нм3/Час •»} = 0,95;
СРь = 0,33 ккал/нм3 - °С с-в - = 22,0 ккал/м2 • °С;
^г. ср:—®в. ср = ^0 С. ^^ = 24808;
— ^ = 6450 лі2.
Если эти значения подставить в уравнение (732), то изменение температуры горячего воздуха
Д;(в2 = 118°С/час.
По результатам измерений это изменение температуры равнялось 120° С (см. рис. 14 названной работы).
. Так как точность измерения значений а, с, в, у, л и температур невелика по сравнению с полученным здесь совпадением результатов измерений и расчета, то такое совпадение надо считать случайностью. Поэтому никаких количественных выводов по точности формул в процентах сделать нельзя. Но практически уравнения (724) и (743) соответствуют требованиям точности. Следовательно, можно провести наиболее важную часть предварительного расчета регенератора, например определить падение температуры горячего воздуха или увеличение температуры отходящего газа, что зависит от массы кирпича, заполняющего регенератор.
Но вопреки прежним предположениям, дело не в том, что регенератор содержит большую массу кирпича или соответственно плотный кирпич, а в том, что вблизи выхода рассматриваемой среды, например воздуха, будут предприняты соответствующие меры; поэтому в формулах, характеризующих падение температуры, выражение х & , р—&в. ір) представляет собой удельную теплопередачу в рассматриваемой точке, например на горячей сто
роне регенератора, а не среднюю удельную теплопередачу по всему регенератору. Аналогично произведение с-Б-уп в этих уравнениях представляет собой аккумулирующую способность кирпича в рассматриваемой точке, а не среднюю величину по всему регенератору. Это, разумеется, справедливо при. том условии, что величина поверхности, зависящей от с, у, т], такая, что появляющиеся в холодной части более сильные изменения температуры вследствие малых значений с, у. Л могли бы затухать. Для этого при нормальных условиях поверхность нагрева должна составлять примерно 20% всей поверхности. В кауперах на горячей стороне разность температур между средами газ—воздух &г. ср—&в. ср большая, а на холодной стороне — ма^ая. Опираясь на выведенные формулы, в результате этого получим сильное падение температуры горячего воздуха и слабое повышение температуры отходящего газа. Поэтому конструктивные мероприятия должны быть направлены на то, чтобы на горячей, стороне использовали болей массивный кирпич с возможно более высокими значениями удельного веса у, удельной теплоемкости с, коэффициента теплопроводности X и с соответствующей степенью использования ть иными словами, с возможно более высокой аккумулирующей способностью с-в-ул - На холодной стороне можно применять почти любой кирпич с небольшой аккумулирующей способностью и с большой поверхностью нагрева каждого квадратного метра. Следовательно, 1 м2 поверхности нагрева характеризуется не только весом кирпича, но и потребностью пространства тем в большей степени, чем толще кирпич. С другой сто. роны, общая поверхность нагрева решающим образом влияет на коэффициент полезного действия регенератора. В этом разделении аккумулирующей массы и поверхности нагрева лежит экономическое значение многозонного воздухоподогревателя, который, следовательно, экономически более выгоден, чем однозонный с равной аккумулирующей способностью и равной поверхностью нагрева каждого квадратного метра по всей высоте нагревателя.

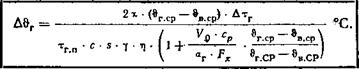
 Опубликовано в
Опубликовано в