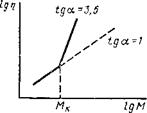
Для полимеров, молекулярная масса которых М>МК (Мк ха­рактеризует размеры отрезка цепи, определяемого физическими узлами молекулярной сетки полимера, ответственными за вязкое течение), при измерениях вязкости в условиях простого сдвига в статическом режиме нагружения оказывается справедливым соот­ношение г] = АМ3>5 (где А — постоянная для полимеров данного ви­да). Обычно самое низкое значение Мк = 4000 у линейного полиэти­лена, тогда как у ПС значение Мк на порядок выше (4-104).

Расстояние между узлами сетки полимера Ме связано с Мк со­отношением Мк = 2Ме. Значение Ме обычно определяется из дина­мических измерений. Из рис. 6.3 следует, что если М<МСу то t]~М*, а если М>МК, то М3>5, Для олигомеров М<МС, а для полимеров, для которых характерна связанная с энтропийным эф­фектом способность к большим обратимым деформациям, М^МК.

Структурирование полимеров приводит к образованию сетки, связывающей их макромолекулы между собой и определяющей проявление ими высокоэластичности. Если известны основные зна­чения (Мк и Ме), то все линейные полимеры можно нормировать (разделить на эти величины), ибо только начиная с этих значений появляется аномалия вязкости, обусловленная появлением струк­туры. По нормированным значениям можно производить класси­фикацию полимеров и определять значение их кинетического сег­мента течения (по Эйрингу). При М = 20Ме и М=Мк завершает-

ся формирование признаков высокополимерного состояния и уве­личивается однородность надмолекулярной структуры (развитие плато высокоэластичности).

У линейных полимеров узкого молекулярно-массового распре­деления проявляются следующие особенности: а) при изменении молекулярной массы от Мк до 3Мк начинает существенно прояв­ляться неньютоновское течение полимеров, т. е. их вязкость при повышении напряжения Р уменьшается; б) у полимеров с более высокими значениями М наблюдается ньютоновское течение, раз­рыв или отрыв от поверхностей ограничения (стенок) и явление сверханомалии вязкости [18; 6.1].

Когда структура полимера становится однородной, при скоростях происходит медленное течение и перемещение центров тяжести макромолекул, как у простых жидкостей, а при больших напряжениях Р оно распределяется по узлам структуры, вызывая, как и у резины, скольжение по стенкам (при этом критическое зна­чение ук зависит от М). В случае полидисперсного полимера кар­тина будет иной, но также имеет место проявление критического напряжения Рк. Для линейных полимеров характерна сложная за­висимость вязкости от М, причем значения ц при значениях М ни­же и выше Мк отличаются. Сверханомалия вязкости отчетливо проявляется в случае узких распределений М, а для полимеров с широким распределением молекулярной массы проявляется суще­ственная зависимость y=f(M) и более размытое явление сверх­аномалии [6.7]. При этом и для последних существует критическое напряжение, выше которого установившееся течение становится невозможным.

При динамическом режиме кроме сдвиговой вязкости измеряют модуль упругости G' и модуль потерь G". Для сравнения полиме - ов по их вязкостным характеристикам (оно проводится при тем - ературах на равной удаленности от соответствующих Тс) важна х нормировка. Для сравнения нужно брать соответствующие ве - ичины при одинаковых отношениях Т/Тс и М/Мк в случае узкого* аспределения молекулярной массы; приближенно это возможна для широкого распределения по молекулярной массе. Важность измерения при разных частотах определяется тем, что наличие- максимумов на температурной и частотной зависимостях G" дает более однозначную характеристику резкого изменения свойств полимеров.

В случае динамического режима нагружения справедливы сле­дующие соотношения для модулей сдвига G' и круговой частоты 0:

0=0,40'; O’max=0,46O'max; % *>max=f{T, M).

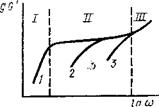
Высота максимума G" не зависит от М, а его положение па Шкале со и Т зависит от М3>5. Положение максимума на кривой g G"=f(u>) для узкого распределения определяется молекулярной ассой полимера: lg Gmax =А—1 (чем больше М, тем

больше глубина минимума). Минимум будет сдвигаться по частот­ной шкале, что отвечает соотношению lgcomin=fi—lg(M/AfK). Фи­зический смысл минимума на зависимости lgG/7=/(со) связан с появлением первых признаков потери сегментальной подвижности или началом перехода в стеклообразное состояние. Этот минимум^ как и максимум tg6=/(co), появляется раньше, чем область плата на зависимости lgG' = /(co). Для полидисперсного полимера эта плато не будет горизонтальным, а максимумы G" и tg 6 являются* более размытыми.

При выполнении условия у=ы имеет место корреляция между модулем G и сдвиговым напряжением Р. Значение этой корреля­ции состоит в том, кто характер кривых течения можно прогнози­ровать по результатам динамических измерений и наоборот [72]..

При динамических измерениях по зависимостям lg G lg G" = = /(0) можно установить область перехода полимеров из однога деформационного физического состояния в другое (рис. 6.4). Осо­бенно отчетливо это проявляется, когда М = 20 Ме. Если М=Ме, то плато высокоэластичности на зависимости lg G7 = /(0) практи­чески не проявляется. Переход в высокоэластическое состояние всегда реализуется при напряжениях Р=105~106 Па. Кривые 1, 2+ 3 на рис. 6.4 и 6.5 соответствуют различным значениям нормиро­ванных молекулярных масс М/Ме. Установившееся течение разных полимеров при сдвиговых напряжениях реализуется при Р = = 104-106 Па.

Из сопоставления представленных на рис. 6.4 и 6.5 кривых lg Gx = /(lg со) и lg G,,=/(lgco) видно, что последние кривые пред­почтительнее для количественной характеристики условий перехо­да полимеров из вязкотекучего состояния в высокоэластическое

{по максимуму) и в стеклообразное (по минимуму). Условия Р = const и Y = const в неустановившемся процессе течения поли­мерной системы отражают различия в ее поведении при разных режимах испытания. При этом не имеет существенного значения, жаким путем достигается установившееся течение, так как между

Рис. 6.4 Рис. 6.5

Рис. 6.4. Зависимость логарифма динамического модуля сдвига G' от лога­рифма частоты со:

/—для М=20Ме; 2 — для Af=5Afe; 3 — для М—Ме; I, II, /// — области соответственно

-вязкотекучего, высокоэластического и стеклообразного состояний полимера

Рис. 6.5. Зависимость логарифма модуля потерь G" от логарифма частоты со:

/ — для М=20Мв; 2 —для ЛГ=5Мв; 3 — для М—Ме

.скоростью деформации вязкого течения у» напряжением сдвига Р ш вязкостью установившегося течения ц = Р/у имеется вполне од­нозначная связь.

В случае деформации одноосного растяжения, как и при про - ютом сдвиге полимеров с узким распределением, при больших, М вязкость ц постоянна. Разрыв образцов таких полимеров проис­ходит при Рраст> 105-т-106 Па. Зависимость т] = f(M) для разных полимеров такая же, как и при сдвиге: т^М1 и г]~М3»5. Так как энергии активации обоих этих процессов (течении при сдвиге и растяжении) одинаковы, есть основание считать, что в данном случае будут проявляться те же основные закономерности, что обусловлено сходством молекулярного механизма течения. Следо­вательно, фундаментальные физические закономерности при рас­тяжении будут теми же самыми, что и при простом сдвиге.