Работа энергетической системы источник питания — сварочная дуга — ванна протекает устойчиво, если источник доставляет до­статочное количество энергии для процесса сварки и покрытия по­терь в системе. Возникающие при горении дуги возмущения наруша­ют устойчивое состояние системы и вызывают переходные процес­сы, характер и скорость протекания которых связаны с энергией, накопленной в магнитных и электрических полях системы, а также энергией, переходящей в тепло. Если после прекращения действия возмущения система возвращается в исходное равновесное состоя­ние, то равновесие является устойчивым, если не возвращается — неустойчивым. При возвращении системы после окончания действия возмущения в состояние равновесия могут наблюдаться отклонения величин, характеризующих режим сварки (тока, напряжения), от: их значения до начала действия возмущения. Если при наличии этих отклонений качество сварного соединения остается в допустимых пределах, то свойства энергетической системы признают удовлетво­рительными.

Современная сварочная техника использует для питания дуги кроме хорошо известных источников питания (трансформаторов, коллекторных генераторов постоянного тока) источники нового ти­па, имеющие корректирующие обратные связи по энергетическим параметрам (ток, напряжение), предназначенные для создания ус­ловий устойчивого горения дуги и поддержания установленного ре­жима. Такие обратные связи имеют источники питания для сварки как плавящимся, так и неплавящимся электродом, как на посто­янном, так и на переменном токах. Благодаря корректирующим обратным связям 6 энергетической системе создаются условия для возникновения воздействия, направленного на подавление возму­щений, возникающих в процессе сварки.

Устойчивость горения сварочной дуги при малых отклонениях напряжения на дуге. Влияние формы внешней статической харак­теристики источника питания и формы статической вольт-амперной характеристики дуги на устойчивость горения дуги впервые было показано в исследованиях Кауфмана [2], который установил, что ду­га постоянного тока данной длины, с падающей вольт-амперной ха­рактеристикой при малых токах, переходящей в пологопадающую, горит устойчиво при питании от генератора с постоянным выходным
напряжением лишь в том случае, когда последовательно с дугой включено определенной величины добавочное сопротивление R. Ус­ловие устойчивого горения дуги было записано в форме следующе­го неравенства:

(Шд/d / -}-•??> О, (1.10)

где dUjJdl—производная вольт-амперной характеристики дуги в данной точке, a R — добавочное резистивное сопротивление в цепи дуги.

Дальнейшее развитие этот вывод получил в работах В. П. Ники­тина [9], И. Я. Рабиновича [11], К. К - Хренова [15], Ю. П. Петрунь - кина (1934) и ряда других авторов применительно к специальным генераторам, имеющим падаю­щую внешнюю характеристику.

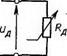
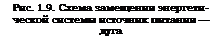В работах [9, 11] выявляются условия, при которых дуга горит устойчиво, не переходя в другие виды электрического разряда, при питании от генератора постоянно­го тока,- имеющего падающую внешнюю характеристику. Сдела­но предположение, что вольт-ам­перная характеристика дуги так­же падающая. Обе характеристи­ки являются нелинейными зависимостями напряжений от тока I. Для генератора это U—f(I), а для дуги UR—f(I). Сделано также предположение, что сварка производится вручную плавящимся электродом, что дуга горит стационарно и замыканий дугового про­межутка каплей не происходит. На рис. 1.9 приведена электриче­ская схема замещения энергетической системы источник питания — дуга. Источник питания не имеет корректирующих обратных свя­зей. Дуга замещена нелинейным резистивным сопротивлением Rn. На схеме Е — э. д. с.; R0 — внутреннее сопротивление генератора;

— резистивное сопротивление сварочного контура, включающее и сопротивление вылета электрода; L — индуктивность сварочного контура. Условные положительные направления токов и напряже­ний здесь и далее указаны стрелками.

На рис. 1.10 приведены внешняя статическая характеристика ге­нератора U=f(I) и вольт-амперная статическая характеристика ду­ги t/H=f(7). Эти характеристики имеют две точки пересечения В и А, которые являются точками равновесия энергетической системы, когда при данном значении сварочного тока /р Ur>=UR. r> (токи и напряжения, соответствующие состоянию равновесия, записаны с индексами «р»: /рВ; /рЛ; t/pB; UvA; Uд. рВ; Дд. рл). Выясним, какая из точек пересечения характеристик является точкой устойчивого рав­новесия, т. е. при каких условиях при малом изменении, например, длины дуги, вызвавшем изменение тока и напряжения, система в состоянии поддерживать устойчивый дуговой разряд. Составим для сварочного контура уравнение по второму закону Кирхгофа. Ис­
пользуя схему рис. 1.9 и обходя контур по условному положительно­му направлению тока і, получаем

et=iR — и--иА. (1-11)

Если учесть, что | <С ^ь, a eL=—Ldi/dt, получим

« = йд + Ldi/dt. (1.12)

Из уравнения (1.12) следует, что

di/dt=(u, — ua)/L, (1.13)

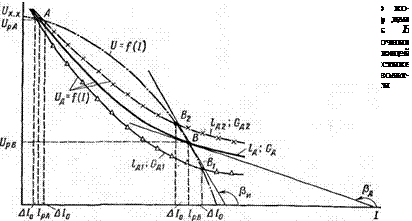а это значит, что скорость изменения сварочного тока во время пе­реходных процессов в энергетической системе тем меньше, чем боль­ше индуктивность сварочного контура. Когда энергетическая систе­ма в равновесии, то и=ип при допущении, что R = 0, di/di = 0.

При данном токе в цепи дуги /=/р в точке пересечения внешней характеристики генератора и статической вольт-амперной характе­ристики дуги и~ил (U — это Up, a Un — это (Уд. р).

Исследуем на устойчивость горение дуги при токе 1рв и напря­жении Uрд, т. е. в точке В пересечения характеристик, соответствую­щих длине дуги /д и проводимости G разрядного промежутка (рис. 1.10). Допустим, что в некоторый начальный момент времени ^ = 0 возникло возмущение по длине дуги. Длина дуги стала /д2, причем /д2>^д - Длине дуги /д2 соответствует уже другая вольт-амперная ха­рактеристика дуги. В новых условиях уменьшилась проводимость G разрядного промежутка Gn2<GK, что явилось причиной уменьшения тока /Рв на Д/0. В последующие моменты времени малое отклонение тока Д/0 будет изменяться во времени. При изменении тока в энер­гетической системе возникает переходный процесс и все величины, связанные с током, изменяются. Для аналитического исследования процессов, протекающих в энергетической системе генератор — сва­

рочная дуга, возникающих при малых отклонениях тока (А/) вбли­зи точек равновесного состояния системы, в технике пользуются ме­тодом линеаризации нелинейных функций U=f(I) и Ua=f(I) вбли­зи точек В и А. Небольшой участок ([17] нелинейной характеристики заменяют отрезком прямой, касательной к соответствующей нели­нейной характеристике в точке равновесия. В литературе [9, 11] делают, кроме того, еще два допущения: исключают влияние дина­мических свойств сварочного генератора и не учитывают явления саморегулирования дуги при сварке плавящимся электродом при небольших плотностях тока, что позволяет рассматривать этот про­цесс сварки как эквивалентный процессу с неплавящимся электро­дом. Применяя метод линеаризации при малых отклонениях от ус­тановившегося состояния [10,12], выражают напряжения генератора U=f(I) и дуги Un—f(I) через их значения при равновесии Uv и Uav и при приращении тока А/, разлагая нелинейные функции U=f(Iv+ +А7) и (7д=Д/р+А7) в ряд Тейлора по степеням А7. Отбрасывая члены ряда второго и больших порядков, получают выражения для напряжения дуги и генератора вблизи точки равновесия В:

7/д=7/д. р+Д7/Д)Р=7/,р+(^/=/рД7 = 7/л. р+7?диф. дД7; (1.14) 7У = 7Ур + Д7/=7/р + (-^)/в/рД7 = 7/р+7?дифд7, (1.15)

где 7?диф. д и 7?диф — дифференциальные сопротивления соответствен­но нелинейного участка электрической цепи с дугой и генератора при 7=7Р (напомним, что индекс «р» означает в данном случае рав­новесное состояние при отсутствии возмущения).

Для получения закона изменения приращения тока Al=f(t) сле­дует подставить в исходное дифференциальное уравнение (1.12) вместо и и цл их значения, соответствующие равновесному состоя­нию энергетической системы (имеющей в качестве источника энер­гии генератор постоянного тока), т. е. U и t/д, которые в равновес­ном состоянии равны, а затем вместо производной сварочного тока

(7р+Д7). Проделав эти преобразо­

вания, получим

L4r+{R-Ф-д-^Ф)д/=0- (1Л6)

Если рассматривать разность дифференциальных сопротивлений как дифференциальное сопротивление системы генератор — дуга (7?дИф. с) и допустить, что величина индуктивности L, включенная последовательно с дугой, не зависит от значения сварочного тока, то можно получить линейное однородное дифференциальное урав­нение первого порядка, описывающее переходный процесс измене­ния Al=f(i):

д/=о. (1.17)

d t. L к ’

Корень характеристического уравнения дифференциального уравнения (1.17)

Т

где т — постоянная времени цепи, равная L/Ддиф. с. После решения уравнения (1.17) получим закон изменения AI = f (t):

А1=А10е~*! (1.18)

В реальных условиях величина индуктивности цепи сварочного тока L>0. Для того чтобы при t-yoo приращение тока затухало (Д/-Я)), необходимо, чтобы Ддиф. с было больше нуля. Возникшее приращение А10 затухает, если р<0.

В литературе [10, 12] дифференциальное сопротивление энерге­тической системы источник питания — дуга обозначают % и назы­вают коэффициентом (критерием) устойчивости, для которого мож­но записать:

Ку = ^диф. с = - Ядиф. д — ^диф = — 77~)/=/р - (1Л9)

Условием устойчивости горения сварочной дуги без корректиру­ющих обратных связей является неравенство

ку> 0. (1.20)

Рассмотрим на конкретном примере, устойчиво ли горит дуга в ■случае ручной дуговой сварки при малых отклонениях сварочного тока в точке равновесия В пересечения падающих статических ха­рактеристик источника и дуги. В качестве источника питания принят генератор постоянного тока, в сварочный контур которого последо­вательно с дугой включена индуктивность.

Для точки В дифференциальное сопротивление дуги (dUK/dI)i=ip =tg рд<0, так как угол |3Д тупой (рис. 1.10). Пусть, на­пример, р = 160°, tg рд=—0,36. Дифференциальное сопротивление источника. dU/dI=tg ри= —1,73. Дифференциальное сопротивление энергетической системы 7?диф. с = Ддиф, д—^?диф. и = —0,36—(—1,73) = = 1,37. Следовательно, в точке пересечения характеристик дуги и источника питания коэффициент устойчивости ку>0. Возникшее от­клонение сварочного тока затухает. Скорость затухания малого ■отклонения тока зависит от абсолютного значения ку и величины Л1о, что следует из выражения

Дадим физическое толкование критерию устойчивости ку. Допу­стим, что при горении дуги, когда 0Р было равно (Уд. р, произошло отклонение сварочного тока / от значения /р до (1рВ—А10). Измене­ние тока вызовет появление э. д. с. самоиндукции в индуктивности L, включенной в сварочный контур генератора. Э. д. с. самоиндук­ции складывается с напряжением генератора. Напряжение на раз­
рядном промежутке возрастает, что вызывает увеличение напряжен­ности электрического поля в разрядном промежутке. Ток вследствие этого возрастает до значения 1рв. Горение дуги устойчиво. Для точ­ки В коэффициент ку>0.

Определим коэффициент устойчивости для точки А. Из рис. 1.10 следует, что

Коэффициент устойчивости Ку для точки А меньше нуля и равновес­ное состояние энергетической системы неустойчивое. Если при горе­нии дуги произошло по какой-либо причине увеличение тока, то - ток будет возрастать до тех пор, пока не достигнет значения 1Рв » пока напряжения U=f(I)I==i9B и £/д=/(7)/=ірВ he станУт равны­ми. Если же ток 1рА уменьшился на Д/0 (влево от точки А на рис. 1.10), то он будет уменьшаться до тех пор, пока дуговой разряд не - прекратится из-заі недостаточной напряженности электрического по­ля в разрядном промежутке.

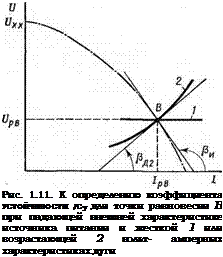
Определим ку для точки В пересечения падающей внешней ха­рактеристики источника питания U=f(I) с жесткой и возрастающей вольт-амперными характеристиками дуги (рис. 1.11). Дифференци­альное сопротивление дуги в точке В для кривой 1 равно нулю, так как (dVjJdl) 1==1В =0, а для кривой 2 (dU^jdI)i=iв>0.

Определив ку по (1.19), получаем, что коэффициент устойчиво­сти системы в рассмотренных конкретных условиях работы положи­телен для обоих случаев.

Допустим, что вольт-амперная характеристика дуги возрастаю­щая (см. рис. 1.7, в). Тогда, как следует из (1.19), коэффициент устойчивости ку получается положительным, если источник питания имеет падающую, жесткую и возрастающую внешнюю характери­стику; в последнем случае при условии, если

dU„ I. dU і д/ |'-'рв дI

Однако практика показывает, что при питании дуги от источника с жесткой или пологовозрастающей внешней характеристикой про­цесс сварки протекает более устойчиво, чем при питании от источ­ника с падающей и особенно крутопадающей внешней характери­стикой. Это объясняется следующими причинами: 1) при выводе вы­ражения ДЛЯ определения Ку были сделаны допущения О ТОМ, что источник энергии (генератор) безынерционен, и 2) не учитывалось явление саморегулирования сварочной дуги. Фактически процесс сварки плавящимся электродом был заменен процессом с неплавя - щимся электродом. В подтверждение можно привести пример, хо­рошо известный технологам-сварщикам. При сварке под флюсом устойчивость горения дуги выше, если источник питания обладает жесткой или возрастающей внешней характеристикой, а не падаю­щей характеристикой.

Выполнение неравенства ку>0 является необходимым, но недо­статочным условием устойчивого горения сварочной дуги при сварке плавящимся электродом.

Современные источники питания для сварки неплавящимся и плавящимся электродом имеют корректирующие обратные связи, обеспечивающие устойчивое горение дуги и установленный режим

или используются источники питания параметрического ти­па ( см. гл. 6).

Эластичность дуги. Для

устойчивости горения дуги важ­ное значение имеет эластич­ность. Дуга считается эластич­ной, если дуговой разряд про­должает существовать при от­носительно значительном уве­личении длины дуги, вызван­ном разными технологическими причинами. Исследования пока­зали, что при данных физико­химических условиях существо­вания дугового разряда в зави­симости от плотности тока су­ществует некоторый минималь­ный ток дуги, при котором ду­говой разряд становится не­устойчивым, а при дальнейшем уменьшении тока переходит в недуговые формы. Эластичность ду­ги оценивают и количественно. Критерием эластичности дуги явля­ется ее наибольшая длина /ДМакс, при которой еще сохраняются условия для устойчивого дугового разряда. При этом ток в сва­рочной цепи, несмотря на значительные отклонения от /р, все же ос­тается больше минимального тока /д мин, при котором меняется вид электрического разряда. При токе /</дмин дуга угасает, но про­водимость G разрядного промежутка не равна нулю, что в первую очередь объясняется остаточной ионизацией плазмы, а также эмис­сионной способностью электродов. Величина /дмин зависит от ве­личины сварочного тока при устойчивом горении дуги. Чем больше /, тем при прочих равных условиях дугу можно растянуть на боль­шую длину. Эластичность дуги зависит также от вида характерис­тик источника питания дуги, а также от их взаимного расположе­ния в точке пересечения В, когда Uv= £/д. р при /=/рв, от величины напряженностей электрического поля в столбе дуги и в приэлек - тродных областях от величины эффективного потенциала ионизации столба дуги и величины /дмин от динамических свойств источника энергии и параметров сварочного контура.

Если электромагнитная инерция источника энергии незначитель­на, а его динамические свойства высоки, то при уменьшении тока и увеличении 1Д быстро возрастает э. д. с. источника, благодаря чему
увеличиваются его выходное напряжение, напряжение на разрядном промежутке и напряженность электрического поля в нем. Таким об­разом сохраняются условия для поддержания дугового разряда. Уменьшение сварочного тока вызывает перераспределение энергии: энергия, накопленная в магнитном поле индуктивности (при нали­чии таковой) при токе /р, преобразуется в энергию электрического поля разрядного промежутка вследствие появления в сварочной це­пи э. д. с. самоиндукции, индуктированной при изменении магнит­ного поля, сцепленного с витками индуктивности, включенной по­следовательно с дугой. Э. д. с. складывается с напряжением источ­ника и увеличивает напряженность электрического поля разрядного промежутка.