Закон Гука верея только в начальной стадии нагружения. Ранее при одномерном напряженном состояния да полагали, что материал переходят в пластическое состояние при условии до­стижения максимальных напряжений ЄГ, предела текучести <Ss, й^6&(Т> (см. § 2.1).

В общем случае напряженного состояния возникает вопрос, какая комбинация компонент напряженая определяет переход материала из упругого состояния в пластическое и наоборот, в настоящее время получили широкое распространение два условия текучестис

1) условие максимального касательного напряжения (усло­вие (условие Трескаг-Сен-Веваяа), когда выполняется одно или два из трех равенств:

IV*aM5 JVSHs HV6*NS, (7.II)

где б1 ,0^,63 - главные нормальные напряжения (зто усло­вие текучести использовалось ранее в подпараграфе 4.7.5);

2) условие постоянства интенсивности напряжений (усло­вие Мизеса)

6t*A, (7.12)

где б; - интенсивность напряжений, равная

бГ^ iferbyf+(бf 62f+(V6xf + 6(г|у+ г+т|х) -=

• (7.13)

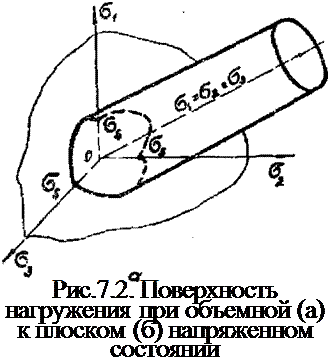
Уравнение (7.II) описывает поверхность правильной ше­стигранной призмы, а (7.12) - поверхность кругового цилиндра с осями, равнонаклоненяши к коордннатнш осям о, , 0г t о. (рас.7.2). Эти поверхности назкважтгсЕ поверхностями нагруге-
шя (яли поверхностями течения). Они отсекает на осях 64 •,

, 63 отрезки длина 6Ь.

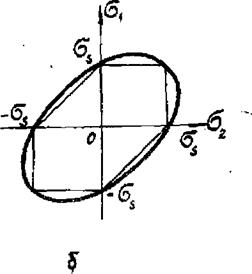
При плоском напряженном состоянии ( 63 = 0) уравнения (7.II) я (7.12) опнснвает след пересечения поверхностей приз­ма и цилиндра с плоскостью б*бг, которой представляет собой шестиугольник и эллипс (ряс.7.2,б).

В общем случае условием Мизеса (7.12) пользоваться удоб­нее» чем условием ТрескагОзв-Венана (7.II). так как не тре­буется поиска максимального касательного напряжения путем пе­ребора напряжений 6{ ,б4, 6Ъ. К тому же для основных конст­рукционных материалов условие Мизеса более точно отражает условие перехода в пластическое состояние. Поэтому в даль­нейшем мв будем пользоваться условием Мизеса. Можно отметить, что разница между двумя условиями невелика (ряс.7.2,б).

Поверхность нагружения в пространстве напряжений отде­ляет при данном состоянии материала область пластического деформирования от области упругого деформирования. Введем Функцию нагружения, определяемую внражением

. (7Д4)

Рассмотрим случай нагружения материала при условии ss(TVconst и б5= О, т. е. примем, что температура материала не меняется, а напряженное состояние плоское. Пусть началь­ное состояние характеризуется точкой 0 (ряс.7.3), б^б^-О.

Нагрузим материал по пути ОМ (напряжения б, и 6^ меняется непропорционально). В конце нагружения материал перевел а

ш

клаета^есйоа состояние (точка М, $ « 0). Далее догрувжм ма- теркая жа d6i£ е где б. б,г - векторная сумма de>, ш d6£ . До­гружение проведем либо к упругой деформащш (разгрузке, еслж вектор d6;2 направлен внутрь области 5<Q )» шбо к

пластической деформации (нагружения, если вектор Аб, г наг-

правлен наружу)„ Приращение d.652 , совпадащео с каеательг - ной к поверхности нагружения (нейтральное изменение), приво­да" только ж уіщутим деформшрш. Последний случай может тттъ да сто, например, если составляющие интенсивности на - щмщвйп& бі перераспределяются, но так, что 6t= const.

Пдаерідность нагружения не является фиксированной, она оцш делается мгковешш (текущим) пределом текучести н зави - сит от текущих температурная условий и все! предшеотвутщей истории деформирования. Здесь возникает вопрос, но какому вшшу изменяется поверхность нагружения при шшстческж дофоркирозакчя <, Подход при определении этого закона, как ж условия возникновения пластических деформаций (7.12), бази­руется на гипотезе "единой кривой". Согласно этой гипотезе воз кржвве деформирования при различная напряженных состоя - киях укладявевтся в одну и ту же ("единую)" кривую в коорди­натах ектсйоввность напряжений - интенсивность деформа - щй рч,

Еі= ~Ъ~І(£х~Ц)*+(£ї”ег)&+(ez~ех)£+ + jfyz+Ігх) ~

е, - главнне динейнне деформации. Так как вид кривой

б^е.^ не зависит от характера (мерности) напряженного со­

стояния, то ее можно определить, например, из опатов на простое растяжение. Вели теперь объединить результати опнтов цри различной температуре, то получим единую поверхность не­изотермического деформирования б^е^Т) и поверхность не - изотермического пластического деформирования 6t= 6s(et, T) „ os - ре делящую условия возникновения и развития пластические формаций в зависимости от температуря и степени деформирова­ния (рис.7.4). Поверхности нагружения в координатам б, е 6, t

&ъ (оши рис.7.2,а) соответствует одва точка на поверхности пластического деформирований брб* (s; ,Т) (при изотроюкегг ;?*г

рочненнз рацдаврхноегн йш? ружеанл: тшвгos т закещу

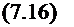йі=б, е,:=е-£0=£-«б0-г.-.1

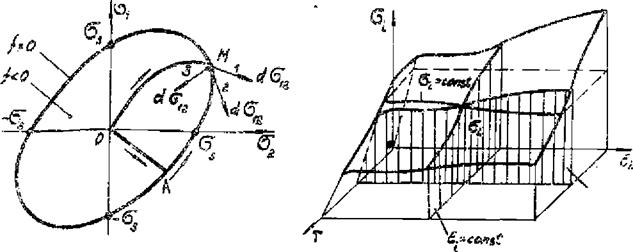Рио.7.4. Поверхность яеизо- термического деформирования

Следует отметить, что, вводя єдину» поверхность пласти­ческого деформирования 6L=6s(tL^ , мы предполагали

справедливость модели изотропного упрочнения (см. § 2.2), со­гласно которой поверхность нагружения равномерно (изотропно) расширяется. Эксперименты подтверждают справедливость моде­ли для относительно несложных путей нагружения, когда плас­тическая деформация развивается преимущественно в одной на­правлении. Например, модель изотропного упрочнения не мохег; отразить эффект Баушингера, который заключается в том, что предварительная пластическая деформация одного знака ухудша­ет сопротивляемость материала пластической деформации обрат­ного знака. Так. пластическое растяжение стержня приводит к

заметному снижению предела текучести при последующем сжатии этого стержня.

Эффект анизотропного упрочнения можно учесть, жестко смещая поверхность нагружения в направлении деформирования относительно центра системи координат. Тогда при повторной нагружении в направлении предыдущей деформации предел теку­чести возрастет, тан как произошло упрочнение, а в обратном направлении упадет, так происходит разупрочнение - г - (ш, рис.2.4,а). Следует отметить, что эффект анизотропного упроч­нения значительно усложняет расчетную схему, а главное, тре­бует дополнительных исходных экспериментальных данных о по­ведении материала при соответствующем знакопеременном на­гружении. Учитывая эти сложности, а также незначительное влияние эффекта анизотропного упрочнения при расчете свароч­ных деформаций и напряжений, этим эффектом, как правило, пре­небрегают.