Уравнение деформации идеальной резины
 20 ноября, 2013
20 ноября, 2013  admin
admin Соотношение для опытной проверки идеальности резины можно получить из уравнения (3.31).
Прежде всего можно показать, что объемным членом в выражении (3.31) можно пренебречь, как весьма малым. Так как V2 = = kV0fX мало (k= 10~4 м2/МН), то где V — реальный объем
деформированной резины. Оценка показала, что можно считать (dV/dX)p, T = 0 с точностью, лежащей за пределами ошибок эксперимента. Столь же малым поэтому является и член (dVJdX) Р, т, который в дальнейшем можно не учитывать. Это означает, что резину при растяжении можно считать несжимаемой. В силу этого выражение (3 9Q) упплтттооТСог гг :аст ьъА
(dUxJd't)P}T=VQf — Т (dV0f /дТ)рЛ, (3.33)
причем справа стоят члены, поддающиеся измерению на опыте. Это соотношение позволяет на основе эксперимента решить вопрос о степени идеальности резины.
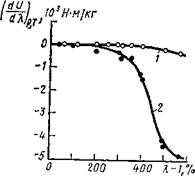
В результате было установлено, что в отсутствие кристаллизации при растяжении ненаполненная резина ведет себя как идеальная почти до разрыва (рис. 3.5, кривая 1), т. е. (dUi/dX)p)T = 0 (но (dU2ldX) Р)т¥= 0). -
После замены в формуле (3.32) энтропийного члена его выражением (3.27) получим для идеальной резины
f=±T(dV0f/dT)M, или (д In l/oF/д In Т)м= 1.
|
|
^0
Рис. 3.5. Кривые, демонстрирующие роль внутренней энергии при деформации (растяжении) резины из натурального каучука (ненаполненная) с 2% серы:
1 — при 80° С (кристаллизация при растяжении не наблюдается); 2 — при 25° С (при растяжениях больше 200% наблюдается кристаллизация)
Из того, что (dVi/dX) р, т=0, и из первого соотношения (3.28) следует, что У0/ не является функцией давления р. Следовательно, In Vof=ln Г+1п[ф(Я)], где ср(Я) —некоторая произвольная функция деформации. Отсюда Уо/=Гср(Я). Таким образом, для идеальной резины характерно уравнение состояния следующего вида:
(3'34)
Vo (Р> т)
Вид функции ф(Я) находится из опыта или методами статистической физики. Иногда удобно условное напряжение f заменить истинным о. Между ними при условии (дУ/дХ)Р, т = 0 существует простая связь o=Xf. Учитывая это, получим
ГГ~~ЯХу(Х)- (3,35)
|
•о-ц |
|
(3.36) |
|
о=Е00(1— 1); /=Е< |
|
где равновесный модуль Есо является функцией температуры и давления, что согласуется с формулой (3.35). |
Из опыта и расчета следует, что ниже 100—200% растяжения наблюдается простой закон деформации сшитого элагтомепя при растяжении:
Чтобы вскрыть физический смысл величин Uu Su определяющих уравнение состояния резины, рассмотрим полимерную сетку без теплового расширения (а = 0) и сжимаемости (£ = 0). Для нее U=U, S — S и соотношения (3.24) и (3.31) совпадают. В этом случае под U и S следует понимать конфигурационные энергию и энтропию, обусловленные изменением конфигурации молекулярных цепей при высокоэластической деформации. Для реального полимера с тепловым расширением и сжимаемостью роль конфигурационных функций состояния играют U и, S. Это следует из того, что нарастание высокоэластичности резины определяется изменением последних, а условием идеальности является не (dU/dk) Р, т = 0, a (dUi/dX)PtT = 0.
Энтропия S2 че имеет отношения к нарастанию высокоэластической упругости резины и поэтому не является конфигурационной энтропией. Действительно, (dS2ldk) РчТ = aV0 (до/дк) V>T = aVoEoo,
если учесть формулу (3.36). Отсюда видно, что (dS2/dk) Р, т не изменяется при изменении конфигурации цепей и вообще не меняет знака при переходе от сжатия к растяжению, тогда как о вместе с (dS]/dk)p, T меняет знак.
Таким образом, термодинамический анализ и результаты опытов позволяют утверждать, что сшитый эластомер при малых и средних деформациях ведет себя как идеальный и высокоэластичностъ име - ei энтропийную природу (в пределах ошибок эксперимента, т. е. с точностью в несколько процентов). Наличие теплового расширения приводит к тому, что напряжение, как это видно из формулы (3.34), не вполне строго пропорционально температуре.
Наличие кристаллизации при растяжении искажает идеальные свойства резины в сильной степени (рис. 3.5, кривая 2).

 Опубликовано в
Опубликовано в