И интервале времени «тц < т < (пхк + Т[) мате­матическая модель регенеративного аппарата описывается систе­мой дифференциальных уравнений переноса энергии (тепла) в по­токе «горячего» теплоносителя и в насадке:

(дТ,. дТ. д'1, дТл

Р |СР. + иь, + Щ, Ъ + Щ,, - ь) =

А дТ, я дТ, я дТ.

"ЕЛ'1Т + г/--?Г+^'-ЯГ: <6-3>

ДО д . 30 . д, 30 , д, 39

Р*>т 1н = тх1'тх + т^щ+т^5,- (6>4)

Здесь п — количество циклов до начала исследуемого процесса; хц — длительность цикла, равная сумме газового Х1 и дутьевого ха периодов; ы>Х1, до,,,, шг< — проекции вектора скорости потока газа в канале регенеративной насадки, полеченные в результате решения гидродинамической задачи; Т —температура «горячего» теплоносителя (дымовых газов); 0—температура насадки; р, X, ср — плотность, коэффициент теплопроводности, теплоемкость го­рячего теплоносителя (с индексом 1) и твердого тела (с индексом т).

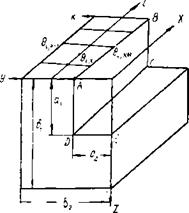
При прямоугольной форме канала для теплоносителей (рис. 6.2) задаем такие краевые условия:

Начальное распределение температуры в твердом теле

Ъ(х, у, г, п, хц) = /| (х, у, г); (6.5)

Граничное условие третьего рода на поверхности АВСД 50 I

= а' аь г% а2* г* х)~ 6(*» а2, г, х]; (6.6)

-X ^ Ктдг

Граничное условие третьего рода на поверхности ДЕКС

= а, (х, г/, а, х) ТI (х, у, аи х) — 6 (х, у, аи х)]. (6.7)

Полагая, что распределение расходов «горячего» и «холодного* теплоносителей по каналам регенеративного аппарата равномер-

Ное, можно ожидать симметричность температурного поля. Тогда в ПЛОСКОСТИ ух при 2 = 0 И 2 = 6]

= 0; — = У Г=и дг

(6.8)

= 0;

Г=Ь,

Плоскости гх при у = 0 и у = -*.£1

(6.9)

= 0.

Ду І!/=0 Начальное распределение тем- ператур в «горячем» теплоноси- теле С момент времени П-ц Т (х, у, г, п-ц) = Ти (6.10) Может быть принято равным тем- пературе «горячего» теплоноси- теля на входе в аппарат. Полученное в результате реше- ния системы (6.3)—(6.4) при кра- сных условиях (6.5)—(6.10) рас- іі ределение температур в твердом теле О [.V, у, г, (/гтц 4- ті)] к момен- ту времени (/г-ц + ті) позволяет перемти к решению задачи пере- носа тепла от насадки к «холод- ному» теплоносителю. В интерва- ле Бремени (ПТц + Ті) < х < (п 4- 1) математическая модель регенеративного теплообменного Аппарата описывается системой уравнений переноса тепла в потоке «холодного» теплоносителя и насадке; /дТ, дТ„ дТ, дТ,

У=Ь,

Рис. 6.2. Элемент объема насадки воздухона гр евател я

ДТ0

_д_ 0/2 а ог2,д <"2. Дх '2 0х ^ ду '2 ду дг 2 дг ' Дь_о дч а, ао а ао РтСрг >т ду Лг ду ~Г дг т дг- Краевые условия запишем аналогично периоду взаимодействия насадки с «горячим» теплоносителем: П[х, у, г, (л-ц + 'сО] =Ь(х, У, 2); (6.12) — ; = а2(*, у, аи х) |0 (л-, у, аи х)— Т-г (х, у, а, г)]; (6.13)

(6.11)

/, I 2 і 01 2 0] 2 . 012) _ Р2Ср* 1“аГ + ^ Ж + ~дї + ~дг) ~

. дп ~Лі^

= 0.2 (х, а-7, г, х) [0 (я, а2, г, г) — Т2(х, а2, г, т); (6.14)

Ф) -'"О!	. дО Ліаі
= 0;	(6.15)
= 0,

Ао _ п _ ■> 50

У=о=0: (6Л6>

'дуц^ь, и’ 'ду

Т2х, У, г, (/гтц + Т|)] = Т2). (6.17)

Здесь а! (х, у, г, т) — распределение коэффициента теплоотдачи от «горячего» теплоносителя к насадке по периметру и длине канала; а2(х, у, г, х)— распределение коэффициента теплоотдачи от насадки к «холодному» теплоносителю по периметру н длине канала. В формулах (6.10), (6.17) Т\, Т— соответственно тем­пературы газа и воздуха на входе в насадку.

Разработанные методы аппроксимации дифференциальных уравнений в частных производных системами алгебраических уравнений [73] позволяют находить чнсленные решения задачи о распределении температуры в потоках теплоносителей и в на­садке. Однако для решения задачи, описываемой системами уравненнй (6.3) — (6.4), (6.11) — (6.12) при краевых условиях (6.4) — (6.10), (6.12) — (6.17), необходимы ЭВМ с большой оперативной и внешней памятью.

Получить расчетное или экспериментальное распределение скоростей в сеченнях каналов регенеративных теплообменных аппаратов достаточно сложно. С учетом существенного прева­лирования одного линейного размера (высота канала) течение теплоносителей можно рассматривать как одномерное, а ско­рость потока определять как среднерасходную по уравнению сплошности.

Тогда математическая модель теплового взаимодействия «го­рячего» потока п насадки примет вид

[дТ, — дТЛ а. (х, т) I

Р, сР| (-^ + -£) = д ■ {Т1 - 0П); (6.18)

ДО д. (30 д . дд /с ш

РтСгт^ = Гх тТх + 'ду 'Гх (6Л9>

В интервале /гхц < х < (пха х^ при краевых условиях

О (х, у, лхц) = /, (х, £/); (6.20)

1 69 1тГу

1Т§ = а, (х, х) [Г, (х) — 0 (дг, а, х)]; (6.21)

= 0 (6.22); Ті (х, лхц) = Гц. (6.23)

!/=*,

Решив систему (6.18)—(6.19) при краевых условиях (6.20)— (6.23) для момента времени (ятц+ті), получим распределение температур в твердом теле как начальное для решения задачи переноса тепла от насадки к потоку «холодного» теплоносителя, описываемой уравнениями (6.19) и

/дТг, - дТЛ а,, (х, т) 2

Р2Ср. Ьг + ^2 ^ (6‘24)

В интервале времени (/гтц + ті) < т < (п + 1) т., при краевых ус­ловиях

(6.25) (6.26)

6[лг, У(тц + ті) = /2(лг, у);

Ае Гу

>тТу

У=а

Ао Гу

I

У=Ь

О (6.27); Т2[х, (піц + ті) = Г2і,

(6.28)

0„ — температура поверхности канала, функция координат времени; и), и»?—среднерасходные скорости «горячего» и «хо­лодного» теплоносителей; Z — периметр канала; 5—-площадь по­перечного сечения канала.

Математическая модель переноса тепла в регенеративном теилообменном аппарате, описываемая системами уравнений (6.18), (6.19) и (6.24) — (6.19) при краевых условиях (6.20) — (0.23) и (6.25) — (6.28), используется для опнсаппя и изучения переходных режимов работы аппарата.