Пузырьки газа, образовавшиеся в сварочной ванне, вследствие разностей плотностей металла и газа будут стремиться выйти на поверхность расплава. Очевидно, что весь процесс удале­ния газового пузырька из сварочной ванны можно разделить на два этапа: перемещение пузырька к границе металл — газ или металл — шлак в зависимости от применяемого способа защиты и переход газового пузырька через межфазную грани­цу. Чаще всего процесс перемещения пузырьков в жидкости

описывают формулой Стокса

2 (рм — Рг) 9 11м

Довольно точно величину скорости перемещения пузырька можно рассчитать по формуле Стокса лишь при Re ^ 2,0. По-видимому, в сварочных процессах, особенно в случаях, когда металл сварочной ванны подвергается интенсивному пе­ремешиванию, использование формулы Стокса приведет к не­верным результатам.

Уравнение (IV.41) справедливо для случая, когда в подни­мающемся пузырьке не происходит циркуляция газа, которая в реальных условиях имеет место. Скорость подъема пузырька при наличии в последнем циркуляции газа может быть опре­делена по формуле

(IV.42)

где т]г — вязкость газа.

Поскольку т)г <£ т]м, расчеты обычно ведут по упрощенной формуле

°=JVLere

Из сопоставления формул (IV.42), (IV.43) с (IV.41) видно, что при наличии в пузырьках внутренней циркуляции скорость движения пузырьков в расплаве увеличивается. Однако урав­нения (IV.41) — (IV.43) справедливы для сферических пу­зырьков.

Между тем известно, что на поднимающийся пузырек, по­мимо сил поверхностного натяжения, которые стремятся при­дать ему сферическую форму, действуют также силы трения и градиент давления жидкости, стремящиеся деформировать пузырек. В конечном итоге форма пузырька будет определять­ся соотношением действующих на него сил, величина которых, очевидно, зависит от размера всплывающего пузырька.

Согласно П55], радиус пузырька, не деформируемого при всплытии, г = (324т)„ ам_г/рtag2)'7', где ам_г — поверхностное натяжение расплава.

В стали форма поднимающихся пузырьков будет сфериче­ской, если их радиус меньше 0,1 • 10“~3 м. Пузырьки большего размера должны деформироваться при подъеме, причем де­формация их будет значительной, если г« Уои^г/(£.

Поскольку в сварном шве обнаруживаются поры диаметром (2—3) • 10~3м, в процессе их перемещения возможна деформа­ция пузырьков. Поэтому для описания движения крупных пу­зырьков в сварочной ванне, очевидно, следует пользоваться формулой Маленкова [132]:

<IV-44>

где гэ — радиус, эквивалентный радиусу сферического пу­зырька.

Формула (IV.44) справедлива для случая турбулентного всплытия пузырька эллипсоидной или грибовидной формы, что подтверждается и экспериментами [23]. Сравнение значений скорости подъема пузырька, определенных по формулам (IV.41) — (IV.44), свидетельствует о том, что деформация пу­зырька приводит к снижению скорости его подъема, а значит, повышает вероятность застревания пузырька в металле шва.

На скорость движения газового пузырька оказывают влия­ние поверхностно-активные элементы, присутствующие в расп­лаве, а также скорость движения других пузырьков. При на­личии в расплаве поверхностно-активных элементов скорость подъема пузырька [269]:

г, — і) Зт)м + з% + Зуі

ст 2тім + Зт, г + ЗТі,

где цСт — скорость подъема пузырька, рассчитанная по фор­муле (IV.41);

Г — адсорбция поверхностно-активного вещества; D — ко­эффициент молекулярной диффузии; С — концентрация по­верхностно-активного вещества.

Поскольку г]р <£ т)м, вязкостью газа можно пренебречь. Тогда выражение (IV.45) примет вид

Из анализа формул (IV.46) и (IV.47) видно, что при отсутствии в расплаве поверхностно-активных элементов или при очень не большом их содержании (С->0) выражение (IV.47) переходит в формулу (IV.43).

Если содержание поверхностно-актив­ных веществ в расплаве достаточно вели­ко, то скорость подъема мелких пузырь­ков должна хорошо описываться форму­лой Стокса. Это связано с тем, что при значительном содержании в жидкости поверхностно-активных элементов за счет адсорбции их на поверхность пузырек — жидкость могут образоваться пленки, которые будут иметь значительную толщину и высокую прочность. Появление этих пленок приводит к тому, что пузырьки начинают двигать­ся аналогично твердым шарикам, движение которых в жидко­сти описывается формулой (IV.41).

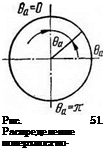
При движении газового пузырька адсорбированные на его поверхности поверхностно-активные вещества будут неравно­мерно распределены на границе пузырек — расплав. В лобо­вой части пузырька содержание поверхностно-активных эле­ментов будет меньше, чем в кормовой. Распределение поверх­ностно-активного компонента на поверхности пузырька в за­висимости от угла 0а (рис. 51) описывается [155] следующим уравнением:

где ДСср — перепад концентрации компонента в диффузион­ном слое; v — скорость подъема пузырька.

Как видно из уравнения (IV.48), с повышением скорости подъема пузырька неравномерность в распределении поверх­ностно-активных элементов на поверхности газового пузырька увеличивается и может достигать значительных величин. По данным [155], при всплывании пузырька аргона на его корме могут создаваться 20—30-кратные пересыщения по N2 и S и 3—5-кратные пересыщения по Оа. Это может ускорить проте­кание реакций и способствовать образованию сульфидов, нит­ридов и оксидов. Таким образом, по-видимому, не только нали­чие неметаллических включений влияет на процесс порообра­зования (см. гл. III), но и наличие пузырька в металле свароч­
ной ванны может способствовать образованию неметалличе­ских включений.

Все рассмотренные закономерности относятся к случаю всплытия единичного пузырька. В реальных же условиях воз­можно одновременное перемещение в расплаве нескольких пузырьков, когда каждый из перемещающихся пузырьков вызывает образование в расплаве течений, которые, действуя на другие пузырьки, будут изменять условия их движения. Изменения эти будут во многом зависеть от формы и размеров сварочной ванны.

В системе, не ограниченной стенками, каждый из пузырьков при своем движении увлекает за собой окружающую жидкость, что приводит к снижению сопротивления жидкости и повыше­нию скорости подъема пузырьков. Для случая параллельного движения двух сфер сопротивление их движению, согласно

М. Смолуховскому, уменьшается в -^-лг^т^цсозу 4- раз (где

z 0П

6П — расстояние между пузырьками; у — угол между лини­ей центров и направлением движения пузырьков; гг и г2 — радиусы первого и второго пузырьков).

При движении частиц в ограниченном пространстве вблизи поднимающихся пузырьков жидкость увлекается вместе с ни­ми, а вдали от них перемещается в обратном направлении. По­этому при движении нескольких пузырьков в ограниченном пространстве скорость подъема их будет меньше, чем при подъ­еме единичного пузырька.

Иногда для расчета скоростей подъема пузырька с учетом ограниченности объема жидкости пользуются формулой Ладен - бурга, полученной для случая перемещения частицы сфериче­ской формы по оси бесконечного цилиндра, радиус которого равен гц, и уточненной Г. Барром [161;

К сожалению, недостаток экспериментальных данных, подт­верждающих справедливость формулы (IV.49), заставляет ос­торожно пользоваться ею для практических расчетов.

Несомненно одно, что во всех случаях при увеличении рас­стояния между всплывающими пузырьками взаимное влияние движения пузырьков снижается. Обычно при всплытии не­скольких пузырьков их взаимным влиянием на движение друг друга можно пренебречь [282], если 6П ^ 2 (2г — In 0,05/-), т. е. примерно при 6П = Юг.

Таким образом, на процесс подъема пузырьков в расплаве влияет наличие поверхностно-активных элементов в расплаве,

Рис. 52. Схема перехода газово - Рис. 53. Схема образования от - го пузырька через границу ме - верстия в пленке по Де Фризу, талл — шлак.

размеры пузырьков и их взаимное расположение, физические свойства расплава, размеры, конфигурация и температура сва­рочной ванны.

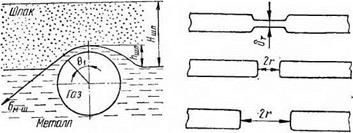
Ранее было отмечено, что для сварочных систем характер­ны два вида межфазных границ, через которые переходят газо­вые пузырьки, удаляемые из сварочной ванны: металл — газ и металл — шлак (рис. 52). Рассмотрим вначале процесс перехода газовых пузырьков через границу металл — газ.

Как показали эксперименты (2841, при приближении пу­зырька к свободной поверхности жидкости происходит изгиб последней. При этом скорость подъема пузырька снижается, а поднятая пузырьком жидкость стекает с поверхности купо­ла. В результате изгиба свободной поверхности жидкости происходит увеличение поверхностной энергии системы, что приводит к большему отклонению системы от равновесия и снижению ее устойчивости.

По данным [284], для стали пленка остается устойчивой, если ее толщина не меньше (0,01—0,02) • 10~3 м, что гораздо больше размеров молекул. Поэтому для описания процесса разрушения металлической пленки, очевидно, справедлива модель разрушения полимолекулярных пленок, разработан­ная Де Фризом. Согласно этой теории, разрушение пленки начинается с образования в ней отверстия (рис. 53), на что необходимо затратить энергию. Это связано с тем, что в первый момент образования отверстия в пленке происходит увеличе­ние поверхности системы, величину которой можно подсчитать по формуле

AS = Л28т (Г mi г, + — 2л |г min + - тг)2 .

где б, — толщина пленки; /тш — минимальный радиус от­верстия.

Наибольшее увеличение поверхности раздела достигается при г = ^ бт. В этом случае

ASmax = (-Х - — Я) 6?—0,736?.

Поскольку увеличение свободной энергии системы при рас­ширении отверстия, или энергия активации А, равна произ­ведению AS на См__________ г (поверхностное натяжение), то

Атах ~ ASmax^M—г О,736^0м—г - (IV.50)

Таким образом, на процесс разрушения пленки в наиболь­шей мере будет влиять толщина пленки, а значит, и факторы, от которых зависит эта толщина.

При выходе газового пузырька на поверхность расплав, находящийся между внутренней и наружной поверхностями пленки (см. рис. 52), будет стекать в сварочную ванну, что при­ведет к утонению пленки.

Обозначим скорость истечения расплава в точке на расстоя­нии х от центра пленки через vn. Силы тяжести расплава, содержащегося между двумя симметричными участками плен­ки, которые находятся друг от друга на расстоянии 2х, уравно­вешиваются силами вязкости [5250]:

— Рм g *=11м-|г - (IV.51)

Проинтегрировав уравнение (IV.50), получим зависимость скорости потока от расстояния х

Vn = ^ (6т - 4х^). (IV.52)

Как видно, с увеличением вязкости и уменьшением плот­ности расплава скорость истечения расплава, а значит, и ско­рость уменьшения толщины стенки уменьшается.

Однако в условиях сварки вследствие быстротечности про­цесса образования сварного шва особое значение будет иметь скорость разрушения пленки. Первым начал изучать процесс разрушения пленки Дюпре. Приняв, что поверхностная энер­гия пленки полностью переходит в кинетическую энергию жид­кости, он получил следующее уравнение баланса энергий:

О С т’р 1 с Я.2

гоп 2 2 АпОтрм0р,

где рм — плотность расплава; S„ — площадь пленки.

Отсюда скорость разрушения пленки

vp = V 4ам_г/рмбт. (IV.53)

Однако результаты экспериментов свидетельствуют о том, что значения скорости, полученные из формулы (IV.53), за­вышены.

Более точно процесс разрушения пленки описывает урав­нение [323], полученное при допущении, что скорость распро­странения круговой волны пк, действующей против сил поверх­ностного натяжения двухсторонней пленки, постоянна и со­ставляет

= У 2ам_г/рп6т. (IV.54)

Разницу в скоростях разрушения пленки, определенных по формулам (IV.53) и (IV.54), можно объяснить следующим об­разом. Как известно, разрушение пленки, согласно схеме Де Фриза, начинается с образования круглого отверстия. При расширении этого отверстия перед краями фронта распростра­няется ореол [323], представляющий собой утолщенную часть пленки. При этом часть кинетической энергии рассеивается и потери составляют примерно 50 % [20, 308].

Из выражений (IV.50), (IV.54) следует, что энергия актива­ции при расширении отверстия и скорость разрушения пленки зависят от величин поверхностного натяжения и толщины плен­ки. При этом, чем меньше величина поверхностного натяжения, т. е. при наличии в расплаве поверхностно-активных элементов, тем заметнее уменьшаются величины энергии активации и ско­рости разрушения пленки. Наличие поверхностно-активных ве­ществ в расплаве делает пленку более устойчивой и затрудняет удаление пузырьков из металла в атмосферу. Это подтвержда­ется экспериментами [247], в результате которых установлено, что в чистой воде пузырек лопается сразу при подходе к поверх­ности. Однако если пузырек был защищен мыльной пленкой, то он сохранялся на поверхности до 10 с. Разрыву пленок спо­собствуют вибрация металла сварочной ванны и его перемеши­вание, газовые потоки, перепад температур и т. д.

Исследование с помощью киносъемки процесса разрушения пузырьков на поверхности воды показали, что при разрыве пузырьков диаметром до 0,1 • 10_3м выброс жидкости не про­исходил, а при разрыве пузырьков диаметром более 3 • 10~3 м образовывалось несколько сотен мелких капель. Очевидно, что в момент разрушения пузырьков на поверхности сварочной ванны также может произойти разбрызгивание материала плен­ки. Если считать газ, находящийся в пузырьке, идеальным, то
при разрушении пузырька может быть совершена работа

А = (Рата + - Ро) Ут ІП {1

где VT — объем пузырька; Р0 = = 2d г.

Если принять Ратм = 0,1 МПа, о = 1000 мДж/м2, то в результате разрушения пузырька радиусом г = 0,1 • 10_3 масса металла 0,41 х X 10 кг может приобрести ско­рость 0,10м/с. Следовательно, раз­рушение газовых пузырей, выхо­дящих на поверхность металл — газ, может стать одной из причин разбрызгивания металла.

При наличии на поверхности сварочной ванны оксидной пленки или слоя шлака при переходе пузырька из металла в шлак вместе с пузырьком, как показали исследования на моделях [47], уносится и металлическая оболочка. Последняя затем превращается в каплю, которая может опуститься в сва­рочную ванну, если еще не успеют закристаллизоваться шлак и металл сварочной ванны. Объем металлической оболочки, уносимый пузырьком, примерно в два раза меньше объема пузырька [171]. Это справедливо для случая всплывания пу­зырьков, отстоящих друг от друга на расстояние не менее 4г.

Очевидно, что процесс перехода газовых пузырей из метал­ла в шлак будет зависеть от соотношения между кинетической энергией поднимающегося пузырька, энергией поверхностного натяжения, которая будет возрастать с увеличением размеров купола (см. рис. 52), и потенциальной энергией столба шлака и металлической оболочки купола. Поскольку толщина металли­ческой оболочки очень мала, ее влиянием можно пренебречь. Тогда условие перехода пузырька из металла в шлак запишет­ся следующим образом:

где цм — вязкость металлического расплава; рг и pmj, — плот­ность газа и шлака соответственно; 0М-Ш — межфазное натя­жение на границе металл — шлак.

Увеличение разности между кинетической энергией и сум­мой поверхностной и потенциальной энергий повышает веро­ятность перехода пузырька из металла в шлак. Следовательно, скорость перехода пузырьков будет увеличиваться с ростом размеров пузырька и с уменьшением величин ом-ш, #шл, т]м, ршл. По-видимому, протеканию процесса перехода газовых пу - пузырьков из металла в шлак будет способствовать переме­шивание металла сварочной ванны, так как при этом должна увеличиться кинетическая энергия пузырька.

Следует учесть, что увеличению размеров купола поднима­ющегося пузыря будут препятствовать и силы вязкости шлака. Поэтому повышение вязкости шлака, очевидно, будет затруд­нять переход газового пузыря из металла в шлак вследствие снижения скорости его подъема [14, 135].

Газовый пузырек, вышедший на границу металл — шлак и энергетически не способный перейти через эту границу, мо­жет разрушиться. При этом вероятность разрушения пузырь­ка будет во многом определяться скоростью удаления распла­ва из зазора между шлаком и газовым пузырьком, которую можно определить из выражения (IV.53).

Наличие потерь металла из сварочной ванны при сварке под флюсом и без флюса подтверждают и результаты эксперимен­тов, проведенных авторами данной монографии следующим об­разом. Пластина из иизкоуглеродистой стали в течение (16,4— 23,9) 10 с расплавлялись угольной дугой без флюса и под флю­сом ОСЦ-45. В последнем случае толщина флюса составляла (3—6) • 10~3м, что обеспечивало наличие на поверхности ме­таллической ванны шлакового покрова.

При сварке без флюса поверхность планок была покрыта мелкими брызгами, диаметр которых в основном не превышал 0,8 • 10”3м, а расстояние от оси валика составляло 1 • 10 1 м и более.

Потери металла, которые определялись по разнице массы пластин до и после сварки, увеличивались с возрастанием силы сварочного тока (см. рис. 54) при сварке с флюсом и без флюса.

Повышение напряжения дуги снижает величину потерь. Так, при (Уд = 30 В и /св = 320 А масса разбрызгиваемого металла составила 11,5 • 10—3 кг. Вероятно, это, как и при уда­лении неметаллических включений, связано с тем, что увели­чение ширины сварочной ванны, которое происходит с увели­чением (7Д, затрудняет удаление пузырей из расплава.

Как было показано, удаление газовых пузырьков из сва­рочной ванны во многом определяется устойчивостью пленки купола металла, образуемого пузырьком при выходе на поверх­ность металлического расплава. Совершенно очевидно, что при сварке в потолочном или вертикальном положении за счет действия сил тяжести скорость истечения металла из пленки будет ниже, чем при сварке в нижнем положении. То же самое наблюдается и при сварке угловых, тавровых и крес­товых соединений по сравнению со стыковыми соединениями. Кроме того, при сварке в потолочном или вертикальном по­ложении, а также при сварке угловых, тавровых и крестовых соединений в нижнем положении подъемная сила, действующая на пузырек, не будет целиком способствовать, а при сварке в потолочном положении будет даже препятствовать выходу пузырька к поверхности металла. Вследствие этих причин по­ристость в швах угловых, тавровых и крестовых соединений, а также при сварке в потолочном и вертикальном положениях будет Еыше, чем при сварке стыковых швов и при сварке в ниж­нем положении.