Анализ вариантов использования квантовых преобразователей дифференциального типа говорит о разнообразии задач, решаемых з различных условиях с их помощью. Рассмотрим ряд важных прак­тических примеров, где без существенного изменения дифференциаль­ной схемы удается получить несколько весьма - полезных эффектоз (усиление-, преобразование фазового сдвига в частоту и т. п.).

Дифференциальные квантовые преобразователи являются преж­де всего помехоустойчивыми устройствами, так как внешние син­хронные помехи в дифференциальных схемах компенсируются.

Эта важная особенность дифференциальных преобразователей при более детальном анализе влияния внешних помех дополняется еще одним, не менее полезным свойством. Оно связано с сущест­вованием зон полной нечувствительности к внешним источникам по­мех, создающим в месте расположения квантовых датчиков различ­ные по модулю наводки. Покажем, что это оказывается справедли­вым в широком спектре частот, практически встречающихся в реаль­ных условиях эксплуатации.

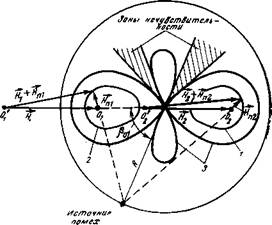
Вид индикатриссы, определяющей влияние внешних магнитных наводок на квантовый дифференциальный преобразователь при по­стоянстве модуля помехи в зоне одного из датчиков, при отсутствии помехи во втором датчике и изменении угла ориентации вектора помехи относительно оптической оси <ро описывается функцией, вы­текающей из формулы (1-25)

т » У Н1 + н - 2Н, нп cos р01 - Н„ (2-31)

где #п — напряженность поля внешней помехи; АН — разность моду­лей поля в зоне датчиков.

Характер индикатриссы в общем случае определяется, исходя из векторной диаграммы на рис. 2-4, и зависит от закона изменения

Рис. 2-4. Характер влияния источников магнитных помех на выходной сигнал преобразователя.

напряженности источника помех в пространстве. Индикатрисса по* мех 3 соответствует случаю, когда источники помех действуют в зо* не каждого из датчиков и имеют разную амплитуду. Точки О і и Ог обозначают центры частотных датчиков. Источник помех перемещав ется по радиусу R. Именение амплитуды помехи в каждом датчикеопределяется внутренними индикатриссами 1 и 2, а девиация частск ты на выходе преобразователя находится в соответствии с соотно^ шением (2-13) по формуле

-1 Я2 + ЯП21) + 2кг (I Я, + Яш| - | Я2 + ЯП2|) Н (2-32)

или, поскольку k2Hi<^ku

Характер кривых Af=f($0) при Яі = const подтверждает факт существования зон, в которых квантовые преобразователи нечувст* вительны к неоднородным помехам типа градиентов поля, создаваем мым близко расположенными электротехническими устройствами.

Особый случай представляет режим работы квантового преобра­зователя, используемого в качестве фазометра, когда внешние гар­монические возмущения в каждом частотном датчике равны по мо­дулю и имеют некоторый фазовый сдвиг. Этот режим может быть создан путем возбуждения колец Гельмгольца датчиков, сдвинутыми по фазе электрическими сигналами с частотой Йі и одинаковой амплитудой іUт.

Частота на выходе каждого из датчиков в соответствии с форму­лой (2-1), если пренебречь для упрощения коэффициентом ki, оказы­вается равной:

f = біЯо + ktf (Um, 2)

или

(2-34)

ktGUm.

fs = * 0 + —£— sin (Q,< +,<p),

где G — постоянная колец Гельмгольца датчика; R — сопротивление его обмотки; Vo — начальная частота в поле Я0.

sin-|-- (2-35)

Разностная частота

Д i = fi — h = — 2fe, t/mcos

T

dt = 2kxUm

sin dt (2-36)

0

Если определить число периодов AM разностной частоты за вре­мя Т, равное периоду низкой частоты Qif то оно окажется пропор­циональным фазовому сдвигу:

T

A^=J| Af I

9 или, при углах у <[30°, когда sin-^-

Т

о

о

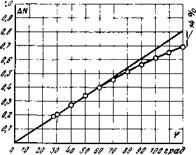
Внешняя характеристика квантового ^фазометра при больших фазовых сдвигах имеет заметную нелинейность, если судить по ре­зультатам расчетов по точной формуле (2-36) (рис. 2-5,а).

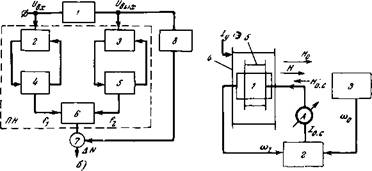
На рис. 2-5,6 показана блок-схема цифрового преобразователя фазы, построенного на основе дифференциального преобразователя

<*)

напряжения ПН, состоящего из двух частотных датчиков 2 и 3 с усилителями в цепи обратной связи 4 и 5, а также фильтра разностной частоты 6. Кванто­вые датчики преобразователя возбуждаются сдвинутыми по фазе сигналами, снимаемыми с входа и выхода контролируе­мого объекта 1. Блок 8 воз­буждается напряжением низ­кой частоты и управляет элек­тронным ключом 7 на входе счетчика импульсов разностной частоты AN.

Полоса пропускания преоб­разователя фазы для цезиевого

Рис. 2-5. Градуировочные кривые Рис. 2-6. Блок-схема системы преобразователя фазового сдви - синхронизации дифференциаль - га (а) и блок-схема цифрового ного квантового преобразова - преобразователя фазового сдви - теля, га (б).

варианта составляет, как следует из табл. 1-2 и (приведенного ниже материала, 100—150 гц и приемлема для ряда практических задач.

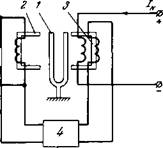
Обратимся теперь к схеме усилителя на основе дифференциаль­ного преобразователя рис. 2-6, в котором использован режим син­хронизации частот (см. § 2-1) и вместо одного из квантовых дат­чиков применен кварцевый задающий генератор 3 с частотой (о0. На рис. 2-6 показан квантовый датчик /, частотный дискриминатор 2, кольца Гельмгольца 4, обтекаемые усиливаемым током /у, и коль­ца 5, обтекаемые током обратной связи /0.с - В цепи обратной связи в установившемся режиме будет протекать постоянный ток. Его

можно определять исходя из условия стабилизации частоты кванто­вого датчика /.

Магнитное чполе в зоне квантового датчика складывается из внешнего поля Н и поля, создаваемого входным током и током в це - пи обратной связи. Если поля коллинеарны, то суммарное поле равно:

Hoi ~ Н “Ь — Я0.с = Н - f* Gj ^ ?/0.с» (2-38)

где Gy, Iy, Ry и Uу — соответственно магнитная постоянная, ток, сопротивление контура, обтекаемого током управления, и напряже­ние на его входе; Н0.с — напряженность, создаваемая контуром об­ратной связи 5 в режиме синхронизации частот.

Поэтому

Uу

со0 = kiH0i = kH -}- kfij ^ ^і#о. с» (2-39)

Откуда

Яо. с = — + Н + G7/j

или

Я k^^H+Gjij

7о. с = q-------- = afj + 6, (2-40)

иО. С ио. С

где

t f„ ®о 1 . Gy

kt ) G0.e » а= G0.e *

Таким образом, квантовый дифференциальный преобразователь при постоянстве коэффициентов а и b может использоваться в режи­ме усиления очень слабых токов, так как отношение магнитных по­стоянных Gy и Gо. с может быть весьма высоким. Постоянная колец

Гельмгольца приближенно определяется по формуле [Л. 72]

(2.41)

где ш—число витков одного кольца; р — средний радиус обмотки в сантиметрах.

Поэтому коэффициент усиления системы при Ь = 0, т. е. при ста­бильном поле Н, определяется в основном отношением числа витков контуров управления и обратной связи.

На рис. 2-7 приведен вид осциллограммы тока в цепи обратной сзязи квантового преобразователя при ряде значений тока на входе контура управления 1У, изменяющегося ступенями через 1 мка.

Частотная характеристика подобного усилителя определяется инерционностью частотного дискриминатора, колец Гельмгольца и спиновой системы. Динамика усилителя описывается уравнениями (2-00)—(2-22), аналитически тождественными уравнениям систем фа­зового регулирования частоты в радиотехнике. Характер экоперименФальной зависимосФи относительгіого изменения уроЁня сигн&Лй на выходе кванторого частотного датчика цезиевого типа от частоты внешнего возмущающего поля для двух камер поглощения (№ 5 и 24) виден из рис. 2-8. Таким образом, квантовый усилитель может

Рассмотрим теперь некоторые способы компенсации внешних по­мех в дифференциальных квантовых преобразователях.

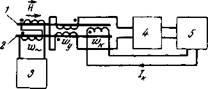
Известно, что в практике геомагнитных исседований для изме­рения напряженности магнитного поля значительное распространение получили феррозондовые измерители (рис. 2-9), чувствительный эле­мент которых выполняется в виде двух малогабаритных пермаллое - вых сердечников 1 .и 2, охваченных рядом обмоток. Специальный ге­нератор 3 с частотой несколько килогерц создает в сердечниках из­меняющееся по гармоническому закону магнитное поле. При наличии в зоне датчика постоянного поля Н (влияющего на цасыщение

Рис. 2-9. Блок-схема феррозондов ого измерителя напряженности магнитно­го поля.

сердечников) на обмотках доу наводится э. д. с. двойной частоты, а э. д. с. первых гармоник компенсируются. Амплитуда э. д. с. удвоенной частоты увеличивается с ростом напряженности постоян­ного магнитного поля. Если сигнал двойной частоты усилить и вы­прямить (в блоках 4 и 5), а затем подать на компенсационную обмотку Док, то постоянный ток в этой цепи будет прямо пропорцио-

нальным проекции вектора Н на направление оси датчика, так как по этому направлению создается встречное компенсирующее поле, не влияющее на ортогональную составляющую поля. В этом случае пермаллоевый сердечник используется в слабо насыщенном режиме и его параметры более стабильны во времени.

В ряде случаев, особенно при явно выраженной направленности внешних помех, оказывается целесообразным использовать простой и весьма надежный феррозондовый измеритель напряженности маг­нитного поля для замены одного из квантовых датчиков в описанных выше дифференциальных схемах квантовых преобразователей, так как последние конструктивно более сложны. Кроме того, использо­вание феррозондовых измерителей вариаций внешнего магнитного поля может позволить снизить требования к экрану преобразовате­ля, увеличивающего вес устройства [Л. 41]. Поскольку феррозондо­вые измерители имеют, как правило, аналоговый (токовый) выход, то для этой цели могут иметь место два способа их применения.

Первый способ предусматривает подачу тока компенсации, про­порционального внешним вариациям, в дополнительные кольца, со­здающие встречные для помех магнитные поля. В этом случае уве­личиваются габариты преобразователя. Подобный прием использу­ется для компенсации помех от аппаратуры самолета при аэромаг­нитных съемках [Другой способ предусматривает компенсацию внешних возму­щений за счет использования феррозондового измерителя, корректи­рующего эталонный генератор частоты. В качестве последнего мо­жет быть использован эталон частоты, имеющийся практически во всех известных системах централизованного контроля.

Рис. 2-10. Камертонный корректор ча­стоты.

На рис. 2-10 показан камертонный генератор эта­лонной частоты, в зоне вет - » вей 1 которого создается дополнительное магнитное f поле, пропорциональное току компенсации /,< [Л. 26.] Ка­мертонный генератор имеет две магнитные системы 2 и 3 и две основные обмотки, одна из которых подключе­на ко входу усилителя 4 в цепи обратной связи, а вторая (возбуждающая)— к его выходу.

Девиация частоты ка­мертонного генератора оказывается пропорциональной току ферро­зондового измерителя /к, изменяющего коэффициент демпфирования колеблющихся ветвей камертона и его частоту. Весьма удобными для решения рассматриваемой задачи оказываются также управляе-

мые кварцевые генераторы.

Принцип действия устройства заключается в том, что основной квантовый частотный датчик генерирует сигнал, часі ота которого оказывается пропорциональной либо угловому перемещению, либо контролируемому параметру. В зависимости от уровня возмущений в обычном дифференциальном датчике имеет место некоторый уход частоты, уровень которого зависит от вариаций градиентов внешнего ноля в зоне преобразователя. Если внешнее поле изменяется в обоих датчиках синхронно, уход частоты оказывается одинаковым и впо­следствии исключается. Однако на практике этот случай встречается редко.

Малогабаритный дифференциальный феррозонДовыи измеритель, размещаемый в непосредственной близости от квантового датчика и ориентируемый по направлению результирующей помехи, умень­шает влияние упомянутых выше вариаций внешнего магнитного ПО' ля. Точность компенсации определяется дрейфом нуля феррозонда Сигнал с его выхода подается на параметрический элемент в цепи настройки кварцевого генератора, изменяя эквивалентную емкость связи резонатора в усилителе цепи обратной связи. Это, как извест­но, приводит к изменению частоты кварцевого генератора [Л. 12] в результате изменения величины реактивного сопротивления, вно­симого в колебательный контур:

(2-42)

А со АСЭ _ т

^КВ 0^0 ()% кВ 0^0

ЩГЛ —т— щГІ

где дХкв/д<х> — степень изменения реактивного сопротивления кварце - всго резонатора генератора; ДСЭ — изменение реактивного сопротив­ления колебательного контура генератора k = AC/AH — коэффициент преобразования генератора.

В качестве - параметрических элементов могут быть использова­ны варикапы или управляемые индуктивности.