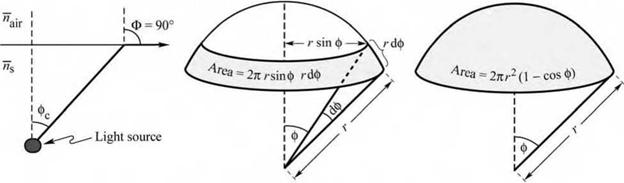
5.3 The light escape cone Light generated inside a semiconductor cannot escape from the semiconductor if it is totally internally reflected at the semiconductor-air interface. If the angle of incidence of a light ray is close to normal incidence, light can escape from the semiconductor. However, total internal reflection occurs for light rays with oblique and grazing-angle incidence. Total internal reflection reduces the external efficiency significantly, in particular for LEDs consisting of high-refractive - index materials.

Assume that the angle of incidence in the semiconductor at the semiconductor-air interface is given by ф. Then the angle of incidence of the refracted ray, Ф, can be inferred from Snell’s law

ns sin ф = najr sin Ф (5.17)

where n s and n air are the refractive indices of the semiconductor and air, respectively. The

critical angle for total internal reflection is obtained using Ф = 90°, as illustrated in Fig. 5.3 (a).

Using Snell’s law, one obtains

nn sin фc = ^ir sin 90° = ^ir (5.18a)

ns ns

and

n

фc = arcsin _^'r . (5.18b)

ns

The refractive indices of semiconductors are usually quite high. For example, GaAs has a refractive index of 3.4. Thus, according to Eq. (5.18), the critical angle for total internal

reflection is quite small. In this case, we can use the approximation sin фе - фе. The critical angle

for total internal reflection is then given by

Фc - ^ • (5.19)

ns

The angle of total internal reflection defines the light escape cone. Light emitted into the cone can escape from the semiconductor, whereas light emitted outside the cone is subject to total internal reflection.

Next, we calculate the surface area of the spherical cone with radius r in order to determine the total fraction of light that is emitted into the light escape cone. The surface area of the calotte-shaped surface shown in Figs. 5.3 (b) and (c) is given by the integral

A = J dA = іф^о r sin ф r dф = 2n r 2(1 - cos ф^ . (5.20)

Let us assume that light is emitted from a point-like source in the semiconductor with a total power of Psource. Then the power that can escape from the semiconductor is given by

P = P 2n r (1 - cos <y (521)

^escape ^source 2

where 4n r2 is the entire surface area of the sphere with radius r.

(a) (b) (c) Fig. 5.3. (a) Definition of the escape cone by the critical angle фс. (b) Area element dA (c) Area of calotte-shaped section of the sphere defined by radius r and angle фс.

The calculation indicates that only a fraction of the light emitted inside a semiconductor can escape from the semiconductor. This fraction is given by

Pescape 1 ^ , 4

(5.22)

= —(1 - cos ф^

P2 1 source z'

Because the critical angle of total internal reflection for high-index materials is relatively small, the cosine term can be expanded into a power series. Neglecting higher-than-second-order terms yields

.2 ^ Фс

.1Ф2 4 Фс

escape

(5.23)

1 -

1 -

2

source

Using the approximation of Eq. (5.19), one obtains

P 1 escape	1	n2 ''air
P 1 source	4	^ СЛ an

(5.24)

The escape problem is a significant problem for high-efficiency LEDs. In most semiconductors, the refractive index is quite high ( > 2.5 ) and thus only a small percentage of the light generated in the semiconductor can escape from a planar LED. The problem is less significant in semiconductors with a small refractive index and for polymers, which have refractive indices of the order of 1.5.

Exercise: Light escape from planar GaAs, GaN, and polymer LED structures. The refractive indices of GaAs, GaN, and light-emitting polymers are 3.4, 2.5, and 1.5, respectively. Calculate the critical angle of total internal reflection for GaAs, GaN, and for polymers. Also calculate the fraction of light power that can escape from a planar GaAs and GaN semiconductor structures and a polymer LED structure.

What improvement can be attained if a planar GaAs LED is encapsulated in a transparent polymer of refractive index 1.5, if the reflection at the polymer-air interface is neglected?

Solution:

Critical angle for total internal reflection:

GaAs фc = 17.1° GaN фc = 23.6° Polymer фc = 41.8°.

Fraction of light that can escape:

GaAs 2.21% GaN 4.18% Polymer 12.7%.

Improvement of the GaAs planar LED due to polymer encapsulation: 232%.