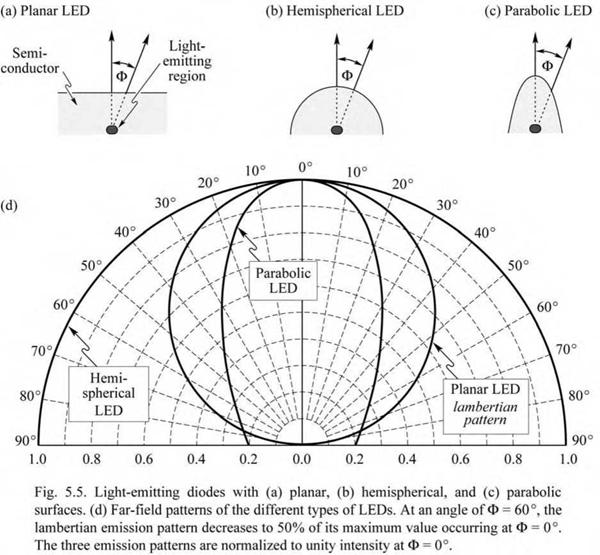
The lambertian emission pattern
 13 марта, 2014
13 марта, 2014  admin
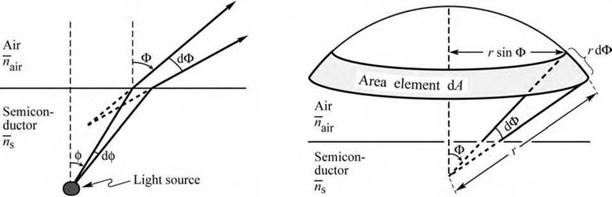
admin The index contrast between the light-emitting material and the surrounding material leads to a non-isotropic emission pattern. For high-index light-emitting materials with a planar surface, a lambertian emission pattern is obtained. Figure 5.4 illustrates a point-like light source located a short distance below a semiconductor-air interface. Consider a light ray emitted from the source at an angle ф with respect to the surface normal. The light ray is refracted at the semiconductor - air interface and the refracted light ray has an angle Ф with respect to the surface normal. The
two angles are related by Snell’s law, which, for small angles of ф (for which sin ф « ф), can be
written as
ns ф = najr sin Ф. (5 .26)
Light emitted into the angle dф in the semiconductor is emitted into the angle dФ in air as shown in Fig. 5.4 (a). Differentiating the equation with respect to Ф and solving the resulting equation for dФ yields
n 1
dФ = ^------------- — dф. (5.27)
|
Power conservation requires that the optical power emitted into the angle dф in the semiconductor be equal to the optical power emitted into the angle dФ in air, i. e. |
najr cos Ф
|
(a) (b)
Fig. 5.4. Geometrical model used to derive the lambertian emission pattern, (a) The light emitted into angle dф inside the semiconductor is emitted into the angle dO in air. (b) Illustration of the area element dA of the calotte-shaped section of the sphere. |
Is dAs = Iair ^air (5 28)
where Is and Iair are the light intensities (measured in units of W/m2) in the semiconductor and air, respectively. Owing to the cylindrical symmetry of the emission pattern we choose the area element shown in Fig. 5.4 (b). The area element in air is given by
dAair = 2 nr sin Ф r dФ. (5 29)
Using Eqs. (5.27) and (5.28) yields
2 n 1
dAair = 2nr —Цг--------------------- ф-- dф. (5.30)
n 2 cos Ф air
Similarly, the surface element in the semiconductor is given by
dAg = 2nr sin ф r dф « 2nr2 ф dф. (5 31)
The light intensity in the semiconductor at a distance r from the light source is given by the total source power divided by the surface area of a sphere with radius r, i. e.
P
Is = . (5.32)
4nr
The light intensity in air can then be inferred from Eqs. (5.28), (5.30), (5.31), and (5.32). One obtains the lambertian emission pattern given by
Psource na2ir
|
(5.33) |
Iair = i™2^ -^cos Ф
4nr ns
The lambertian emission pattern follows a cosine dependence on the angle Ф. The intensity is highest for emission normal to the semiconductor surface, i. e. for Ф = 0°. At an angle of Ф = 60°, the intensity decreases to half of its maximum value. The lambertian emission pattern is shown schematically in Fig. 5.5.
Several other surface shapes are also shown in Fig. 5.5. These non-planar surfaces exhibit various emission patterns. An isotropic emission pattern is obtained for hemispherically shaped LEDs, which have the light-emitting region in the center of the sphere. A strongly directed
emission pattern can be obtained in LEDs with parabolically shaped surfaces. However, both hemispherical as well as parabolic surfaces are difficult to fabricate.
The total power emitted into air can be calculated by integrating the intensity over the entire hemisphere. The total power is then given by
с 90°
Pair = 1Ф = 0° /аіг2пГ sin Ф Г ^ . (5 34)
|
|
By using the lambertian emission pattern for Iair in Eq. (5.34) and using cos Ф sin Ф (1/2) sin (2 Ф), the integral can be calculated to yield
|
Ps |
|
n |
|
air |
|
source |
|
(5.35) |
|
ns2 |
|
4 |
|
P= air |
This result is identical to Eq. (5.24). This is not surprising because the light power that escapes from the semiconductor (Pescape) must be identical to the power in air (Pair).
In the calculation above, Fresnel reflection at the semiconductor-air interface has been neglected. At normal incidence, the Fresnel power transmittance is given by
|
2 |
|
4 ns nair 2 (ns + nair) |
|
f ns nair ^ V ns + nair j |
|
(5.36) |
|
T = 1 - R = 1 - |
Fresnel reflection losses must be taken into account in a rigorous calculation.
Exercise: LED-to-fiber coupling efficiency. Consider a GaAs LED with a point-like light-emitting region located in close proximity to the planar GaAs LED surface. An optical fiber has an acceptance angle of 12° in air. What fraction of the light emitted by the active region can be coupled into the fiber? Assume a GaAs refractive index of 3.4. Neglect Fresnel reflection losses at the semiconductor-air and air-fiber interfaces.
Solution: The acceptance angle in the semiconductor is obtained from Snell’s law and is 3.5°. Thus 0.093% of the power emitted by the active region can be coupled into the fiber.
5.4 Epoxy encapsulants
The light extraction efficiency can be enhanced by using dome-shaped encapsulants with a large refractive index. As a result of the encapsulation, the angle of total internal reflection through the top surface of the semiconductor is increased (Nuese et al., 1969). It follows from Eq. (5.22) that the ratio of extraction efficiency with and without epoxy encapsulant is given by
nepoxy = 1 - cos ^,epoxy (5 37)
nair 1 — cos ^,air
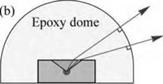
where ф^ертху and ф^ are the critical angles for total internal reflection at the semiconductor - epoxy and semiconductor-air interface, respectively. Figure 5.6 shows the calculated ratio of the extraction efficiency with and without an epoxy dome. Inspection of the figure yields that the efficiency of a typical semiconductor LED increases by a factor of 2-3 upon encapsulation with an epoxy having a refractive index of 1.5.
The inset of Fig. 5.6 shows that light is incident at an angle of approximately 90° at the
epoxy-air interface due to the dome-shape of the epoxy. Thus, total internal reflection losses do not occur at the epoxy-air interface. Besides improving the external efficiency of an LED, the encapsulant can also be used as a spherical lens for applications requiring a directed emission pattern. In polymer LEDs, encapsulants increase the extraction efficiency by only a small amount due to the inherently small refractive index of polymers.
Advanced encapsulants including graded-index encapsulants, encapsulants with a high refractive index (n > 2.0), and encapsulants containing mineral diffusers will be discussed in the chapter on packaging.
|
|
|
о a >> о £ о C с |
|
4.0 |
(a)
Escape cone Light-emitting point
|
1——-- |
j?' li • N L/i * |
3.5 |
|||||
|
Typical |
1 (1 |
||||||
|
і l_ |
. і |
і |
.... |
.... |
і, . . |
iiii |
|
10 9 8 7 6 5 4 л J 2 |
|
Semiconductor with refractive t *:У index ns |
|
1.0 2.0 3.0 Refractive index of encapsulating epoxy n (-) |
Fig. 5.6. LED (a) without and
(b) with dome-shaped epoxy encapsulant. A larger escape angle is obtained for the LED with an epoxy dome, (c) Calculated ratio of light extraction efficiency emitted through the top surface of a planar LED with and without an epoxy dome. The refractive indices of typical epoxies range between 1.4 and 1.8 (adapted from Nuese et a I., 1969).

 Опубликовано в
Опубликовано в