The Computing Environment
 24 февраля, 2014
24 февраля, 2014  admin
admin In computer aided drafting, the computer stores the lines and symbols from the drawing, but does not understand them and cannot interpret them. With wire frame models that store vertices and edges, the computer has some understanding of the geometry and can rotate an object or at least its wire frame representation. However, the ambiguity of wire frames prevents the program from computing some values such as the volume of an object.
|
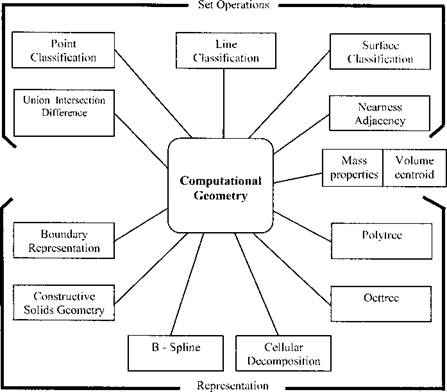
Figure 2-2: The representations and set operations that have been developed for computational geometry are shown above. |
Modem computational geometry has developed representations and operations that overcome these difficulties, Figure 2-2. The best known of these is solids modeling which was developed to provide a mathematically complete representation of the geometry of an object [6].
Mathematicians usually approach geometry from one of two ways. Algebraic topology considers volume in 3D space, e. g., a cube. The boundary of the volume is an oriented surface or set of surfaces of zero thickness. The boundary a surface is a curve. The boundary of a curve is a point. Point set topology considers 3D
space to filled with an infinite set of points. Each point is either inside, outside or on the boundary of a 3D object. An FEM mesh is best treated from the viewpoint of algebraic topology. In FEM analysis of temperature or stress, it is usual to take the viewpoint of point set topology.
Modeling is the process of preparing a computational model. To start creating the analytical model we first have to decide what kind of geometric approximation would be most suitable for our purpose. Figure 2-3 shows several alternatives of geometry.
|
|
|
medium and thick plate |
|
cylinder |
|
|
thin plate
Figure 2-3: Different schemes of idealized body configuration, adopted from [18].
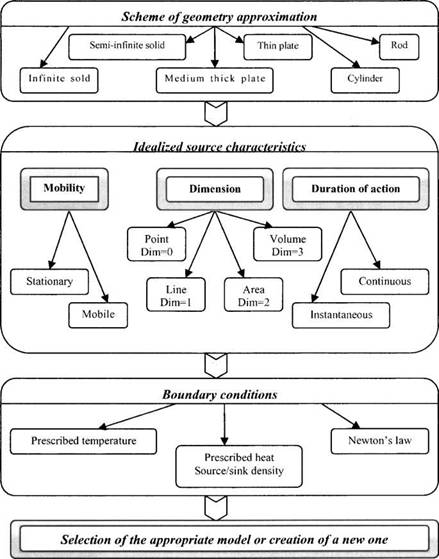
The next step towards analytical model creation is to choose the weld related approximation. Pilipenko [18] suggests the investigated problem can be classified by: time of action, mobility and dimensions. The time of action can be instantaneous or continuous and mobility, stationary or mobile. By the area of distribution, it can be presented as a point (dim=0), line (dim=l), plane (dim=2) and volume (dim=3).
To get a general view, all the classifications are presented in the
Computer Simulation of Welding Processes scheme on Figure 2-4.
|
Figure 2-4: Flow chart of the model selection process, from [18]. |
At present many different analytical models are known. Lindgren presents a review of several in [22]. The earliest numerical predictions of residual stresses were probably those of Tall [21], Vinokurov [76] and Okerblom [75]. Tsuji [23] performed similar calculations. The mechanical analysis was essentially onedimensional, although the analytic solution for the temperatures was two dimensional in the work by Tall. The earliest two-dimensional finite element analysis appeared in the early 1970s, by Iwaki and Masubuchi [24], Ueda and Yamakawa [25, 26 and 27], Fujita et al. [28], Hibbitt and Marcal [29] and Friedman [30]. The early simulations by Fujita et al. [31] and Fujita and Nomoto [32] used only a thermo elastic material model. Although in welding the reality is 3D and transient, and 3D analysis is the most general formulation, to minimize computing costs many analysts have used lower dimensional models. However, they have long sought to perform full 3D analysis of welds. The first analyses of this kind were reported in 1986 [33-35].

 Опубликовано в
Опубликовано в