§3.1. Принципы расчета тепловых процессов при сварке

Теория сварочных деформаций к напряжений примыкает к теории температурных напряжений. В число исходных данных для расчета температурных напряжений непре? ленно входит нестацио­нарное температурное поле. Поэтому в настоящей главе приве­дены некоторые зависимости теории теплопроводности при

сварке, знание которых необходимо для определения текущих

свойств металла сварных соединений и расчета температурных, деформаций и напряжений.

Большинство способов сварки металлических конструкций основано на локальном нагреве металла до плавления (электри­ческая дуговая, газовая, електрошлаковая, плазменная, элек­тронно-лучевая и другие способы сварки). При этом источники нагрева (электрическая дуга, газовое пламя, шлаковая ванна, плазменная струя, электронный луч и др.) характеризуются высокой концентрацией энергии и относительно малой протяжен­ностью. Поэтому вопросы теплопроводности излагаются примени­тельно к таким специфическим источникам теплоты.

Задача теории теплопроводности считается полной, если задан закон теплопереноса, начальное распределение темпера­туры и условия теплообмена на границе нагреваемого тела.

Уравнение теплопереноса устанавливает связь между ско­ростью изменения температуры в любой точке тела с распреде­лением температуры в ее окрестности и в дифференциальной фор­ме имеет вид

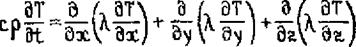(3.1)

где с. р - объемная теплоемкость; А - коэффициент теплопро­водности.

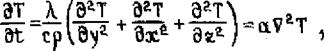Если принять, что коэффициент А не зависит от темпе­ратуры и координат (тело однородно), уравнение (3.1) можно записать в виде

где Vа- - оператор Лапласа; а=А./ср - коэффициент темпера­туропроводности.

Линейное уравнение (3.2) является основным в теории теп­лопроводности, В этой главе будут приведены решения уравне­ния (3.2), отвечающие некоторым частным условиям сварки раз­личных деталей и изделий.

К граничным условиям задачи относятся условия теплооб­мена на границе тела. Если источник теплоты (сварочная дуга) находится на большом расстоянии от границ тела, то принима­ется, что тело имеет бесконечные размеры и температура на его гаснице постоянна и оавна начальной. Если размер тела ограничен, то граница в сварочных задачах принимается, как - повило, адиабатической, т. е. принимается, что тепловой но - . ток через границу отсутствует:

здесь ат/9п - градієнт по нормали к поверхности.

Все многообразие нагреваемых при сварке тел обычно сво­дят к одной из следующих трех схем:

I) полу бесконечное тело, занимающее область г>0

(рис.3.1,а); распределение температуры неравномерно по всем направлениям;

2) бесконечная пластина - тело, ограниченное двумя плос­костями: г. = 0 я д-з • (рис.3.1.,б); распределение темпера­туры по х и у неравномерно и не меняется (равномерно) по

г (толщине);

3)

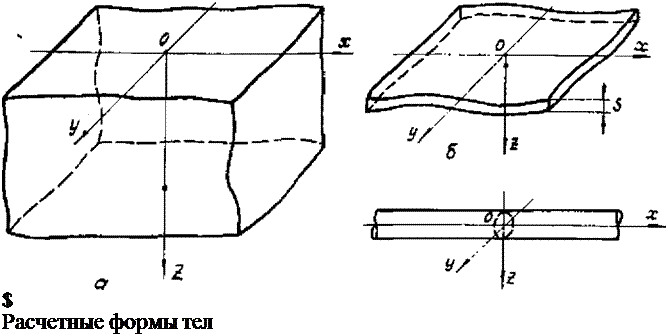бесконечный стержень - тело, распределение темпера­туры в котором неравномерно только по оси х (рпс.3.1.,в).

В случае сварки полубесконечное тело имитирует массив­ное изделие при его несквозном нагреве, бесконечная пласти­на - относительно тонкое изделие при его сквозном проплав­лении. При определенных граничных условиях часто можно отка­заться от неограниченности тел и получать решения для тел, дополнительно ограниченных плоскостями, т. е. для массивного тела ограниченной толщины, пластины ограниченной ширины и длины и стержня ограниченной длины (см. ? 3.6).

Специфическим для задач теплопроводности при сварке яв­ляется то, что в области высокой температуры на температур­ное поле оказывают влияние в большей степени особенности вво­да теплоты (особенности сварочных источников) и в меньшей - граничные условия. Сварочные источники теплоты различаются между собой по распределенности, времени действия и движению относительно нагреваемого тела.

Прежде чем перейти к рассмотрению конкретні» схем, оста­новимся на решении дифференциального уравнения теплопровод­ности (3.2) для неограниченного по всем направлениям тела (бесконечного тела) при наличии мгновенного точечного источ­ника теплоты (элементарного источника теплоты).

Пусть В момент времени t = 0 в точку (Ж,,Г|,г; ) бес­конечного тела помещен мгновенный источник теплоты Q. Тогда температура в любой точке тела (х, у, г, ) в любой момент t определяется по формуле

Непосредственной проверкой можно убедиться, что решение (3.4) удовлетворяет уравнению (3.2). Это решение уравнения теплопроводности называется фундаментальным. Из (3.1) видно, что температура тела стремится к нулю, когда t^O во всех точках, за исключением одной, где она становится

бесконечно большой.

С помощью фундаментального решения (3.4) можно опреде­лить температурное поле от любого сварочного источника теп­лоты в схематизированных телах, пользуясь методом источников. Физическая сущность метода заключается в том, что любой про­цесс распространения теплоты в теле можно представить как со­вокупность процессов выравнивания температуры от множества

элементарных источников, распределенных как в пространстве, так и во времени.

Представим источник теплоты в виде последовательности элементарных мгновенных источников. Определим по (3,4) при­ращение температуры к моменту t от элементарного источни­ка, действовавшего и находящегося в момент г в точке ( т,,

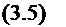exp'

где ^ - мощность источника теплоты; t-t - время распро­странения теплоты. Тогда температура от источника теплоты может быть получена суммированием всех элементарных точечных источников;

d. T(b»di)A;(3.6)

Все приведенные в этой главе решения задач о температур­ном поле при сварке получены методом источников, т. е. путем использования частных форм уравнения (3.6).