Определение переноса теплоты теплопроводностью было дано в § 2.1. Далее даны основные аналитические соотношения процесса теп­лопроводности.

Дифференциальные уравнения теплопроводности. Теория теплопровод­ности является феноменологической теорией, она не рассматривает механизм процесса распространения теплоты, а ограничивается опи­санием этого процесса на основе закона сохранения энергии и закона Фурье.

Дифференциальное уравнение энергии для твердого тела, как было показано выше, принимает вид (2.23):

-~= AV2T + —, (2.63)

Где V2f = + - т~2 + Y2" ~ выражение оператора Лапласа в декар-

Дх ср

Dh d2t Eft дх2 ду2 Ді

Товой системе координат; а - коэффициент температуропроводности,

М2/с.

Если в, теле отсутствуют источники теплоты Q„ — О, то
T(X, у, z, x) удовлетворяет дифференциальному уравнению Фурье:

8T/Dx = AV2T. (2.64)

При стационарной теплопроводности Dt/Dx = 0 и T (х, у, Z) должно удовлетворять уравнению Лапласа

V2t = 0. (2.65)

При стационарном тепловом режиме и наличии внутренних источ­ников теплоты температурное поле описывается уравнением Пуассона

V2T+~~= 0. (2.66) А,

Для одномерного температурного поля, когда температура изме­няется только вдоль оси х, уравнение (2.63) принимает вид

Dt. Па і _ а -------- . (2.67)

Дх дх ср

В цилиндрической системе координат, когда температура изменяется только по направлению радиуса г, уравнение одномерной теплопровод­ности будет

St (D2t 1 Dt qv

— =a ТУ+-Т - + —• 2.68

Дх Dr R Dr J Cp

В сферической системе координат

+ Зі

Дх дг2 R Dr J Ср

Уравнения (2.67) — (2.69) могут быть представлены в общей форме Dt ( D2T Г Dt Qv

Я - М2 + - Г+-' (2-7°)

Дх Drz г Dr J ср

Где г — текущая координата; Г — постоянное число, равное для пластины Г = 0 (г — х), для цилиндра Г = 1 (г = г) и для шара Г = 2 (г = /•).

Я(ігт+- — 1+^-. (2.69)

Для стационарного температурного поля уравнение (2.70) принимает вид

D2t Г dt Dr2 г Dr

DГ* г Dr J ср

Или

5-+ — — J + ^' = 0. (2.71)

Дифференциальные уравнения теплопроводности отражают общий характер процесса, каждое из приведенных уравнений имеет множество решений. Для получения решения, соответствующего конкретной единичной задаче, необходимо задание условий однозначности. В усло­вие однозначности входят геометрические условия, физические пара­метры материала, начальные условия и граничные условия. Условия однозначности содержат описание всех частных особенностей процесса,
которые выделяют единичное явление из всего класса явлений тепло­проводности. Геометрические условия определяют форму и размеры тела, в котором протекает процесс.

Физические условия определяют числовые значения всех физических параметров тела, входящих в дифференциальные уравнения тепло­проводности и граничные условия. При решении задач с внутренними источниками теплоты физические условия характеризуют также знак и распределение величины Qv.

Временные условия или начальные условия определяют температур­ное поле (распределение температур) в начальный момент времени и заключаются в том, что для начального момента времени х0 должна быть известна функция T (х, у, Z, т0).

Граничные условия определяют особенности протекания процесса на границах тела и могут быть заданы следующим образом.

Граничное условие первого рода состоит в задании распределения температуры на поверхности тела в виде функции

Tc = F(X,Y,Z,X). (2.72)

Функция задана в некотором интервале времени, в течение которого изучается процесс. В частном случае, когда температура поверхности постоянна, то Tc = const. Этот случай может наблюдаться при интен­сивном теплообмене со средой (например, при кипении или конден­сации на поверхности тела), тогда температура поверхности Tc может быть принята равной температуре среды 1Ж.

Граничные условия второго рода состоят в задании плотности теплового потока на поверхности тела

Чс = F(X, у, Z, х). (2.73)

В частном случае плотность теплового потока может быть постоянна Qc = const. Этот случай может наблюдаться при нагревании тела внешним электронагревателем или при нагреве излучением в высоко­температурных печах.

Граничные условия третьего рода состоят в задании температуры окружающей среды и интенсивности теплообмена на поверхности тела. Эта интенсивность теплообмена оценивается коэффициентом тепло­отдачи а, а тепловой поток на поверхности пропорционален разности температур окружающей среды £ж и поверхности тела Tc. С другой стороны, плотность теплового потока может быть выражена в соот­ветствии с законом Фурье.

С учетом (2.7) и (2.8) граничное условие третьего рода запишется в виде

129

Граничное условие третьего рода широко используется на прак­тике. В задачах теплопроводности при условии оеД-юо, соответствую­щем условию Bi = (а/)Д -> со, граничные условия третьего рода переходят в граничные условия первого рода. При теплообмене большой интен-

5 А. В. Чечеткин, Н. А. Занемонец
Сивности температура поверхности практически становится равной темпе­ратуре омывающей ее жидкости Tc (т) = Tx (х).

Граничные условия четвертого рода характеризуются равенством тепловых потоков, проходящих через поверхность контакта двух тел:

Г**

При совершенном тепловом контакте изотермы непрерывно пере­ходят из одного тела в другое, а градиенты температур в точках контакта удовлетворяют условию (2.75).

Дифференциальное уравнение теплопроводности (2.63) совместно с условиями однозначности дает полное математическое описание кон­кретной задачи теплопроводности. Решение этой задачи может быть выполнено аналитически, численно с применением ЭВМ или экспери­ментально с использованием методов подобия и моделирования.

Рассмотрим несколько простейших задач теплопроводности.

Стационарные одномерные системы без источников теплоты. В основе решения приведенных ниже задач лежит дифференциальное уравнение энергии (2.24).

Плоская стенка. Граничные условия первого рода. Рассмотрим неограниченную плоскую стенку, толщина которой значи­тельно меньше двух других размеров (рис. 2.5). Такую стенку иногда называют тонкой. Пусть на поверхностях пластины поддерживаются температуры T'C и г", а теплопроводность материала равна X.

При стационарном тепловом режиме Dt/Dx = 0 для одномерного температурного поля, когда температура изменяется только по коорди­нате х и не зависит от у и г, дифференциальное уравнение тепло­проводности принимает вид

D2F/Dx2 = 0. (2.76)

Граничные условия первого рода для данной задачи будут:

При х — 0 T — T'C;

При х = 8 t = t"c. (2J7)

Интегрируем уравнение (2.76) и получаем общее решение Dt/Dx =Си И окончательно

Г(х) = Схх + Съ (2.78)

Где Сі и С2 — постоянные интегрирования, определяемые из граничных условий (2.77).

Полагая х = 0, находим Сг = r'tt а при х = 5 имеем t's=Cxb + T'Ci Откуда Ci = (T"C - T'C)/5.

Подставляя значения постоянных интегрирования в формулу (2.78), получим окончательное решение уравнения (2.76) при граничных условиях (2.77)

T(x) = T'c - (t'c - T"c)~. (2.79)

Из (2.79)

Dt

(2.75) 2

Видно, что T (х) линейно зависит от х. Распределение

Температуры внутри плоской стенки показано па рис. 2.5. Плотность теплового потока при постоянной теплопроводности можно опреде­лить из закона Фурье Q = — XGradT.

В случае неограниченной плоской стенки grad T = Dt/Dx. Значение Dt/Dx было найдено выше и равно Ci = (T"C — T'C)/B. Подставляя значение градиента температуры в выражение закона Фурье, получаем

С-О - (2-80)

Количество теплоты, передаваемое теплопроводностью через по­верхность стенки F, равно

G-yCс-OF. (2.81)

Для многослойной стенки, состоящей из п слоев, при стационарном тепловом режиме значение плотности теплового потока будет постоянно и может быть записано для каждого из слоев следующими соот­ношениями:

Для первого слоя Q = ~~{T'C — Tc t);

1

Для второго слоя Q = -Zr~~(Tc І — Tc ->);

X„ 5 „

(Tc,Ll T C),

Для N-Ro слоя Q

Где Tc, I, Tc.2,... ,Tc, N - температуры между слоями.

Решая эти уравнения относительно температурных напоров, по­лучаем

Рис. 2.5. Стационар­ное распределение тем­пературы в процессе теплопроводности внутри однослойной плоской стенки

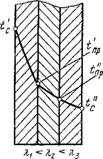
Рис. 2.6. Стационарное распределение темпе­ратуры в процессе теплопроводности в трехслойной плоской стенке при >ч > Я-2 > Х,3

Л<1 > Д"2 д^

Сложив эти уравнения и решив относительно плотности теплового потока, получим

T'C — T'C T'C — T'C

^ 81 Ai + 62Л2 + • • • + 5„Д„ ^ ^ д^ '

I= 1

Где I — порядковый номер слоя.

N

Величина £ (5,-Дг) представляет собой сумму термических сопротив - 1 = 1

Лений слоев стенки R{ = 5,/А-г и называется полным термическим сопротивлением многослойной стенки RCT.

Определив значение Q из (2.82), можно рассчитать температуры между слоями FС, /.

На рис. 2.6 показано изменение температуры в трехслойной плоской стенке при §! = б2 = 53 и > Х2 > ^з, а на рис. 2.7 — при условии Л.1 < Х2 < Х3.

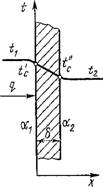
Плоская стенка. Граничные условия третьего рода. Теплопередача. Имеется плоская неограниченная стенка толщиной 5 (рис. 2.8). Заданы теплопроводность материала стенки, коэффициенты теплоотдачи а! и а2 на поверхностях стенки и температуры тепло­носителей, омывающих стенку, Ti и T2. Будем считать, что температуры изменяются только в направлении х, нормальном к поверхности стенки. Тепловой поток при установившемся режиме остается постоян­ным.

Плотность теплового потока от горячего теплоносителя к поверх­ности определяется уравнением теплоотдачи:

Q = *X(Ti-T'J; (2.83)

Внутри твердой стенки по уравнению теплопроводности (2.80):

« = y(fWc); (2.84)

От холодной поверхности стенки к холодному теплоносителю

Q = A2{T"C-T2). (2.85)

Решив совместно уравнения (2.83) - (2.85) относительно плотности теплового потока, получим

QS= ЇМ +V+1/0C2' (2,86)

Дробь - п------------------ г-5—, как было показано выше, обозначается к

^ 1/oci + б/Х + 1/а2

И называется коэффициентом теплопередачи:

K = ------------ - і--------- —. (2.87)

1 /оц + Ъ/Х + Щ2 1 ;

Если термические сопротивления стенки 5/Х и 1/а со стороны тепло­носителей несоизмеримы между собой, то значение коэффициента теплопередачи определяется большим термическим сопротивлением. Для чистой тонкой стенки при 1/cxi 1/а2 коэффициент теплопередачи практически равен меньшему коэффициенту теплоотдачи k ^ at. Интенси­фицировать процесс теплопередачи в этих условиях можно лишь увеличивая интенсивность теплообмена со стороны горячего тепло­носителя.

В случае многослойной стенки в формулу (2.86) следует подстав­лять сумму термических сопротивлений слоев

Ч = --------- Iі ~ t2---------------- —. (2.88)

ЇМ + S (5, А,) + 1/а2 І — 1

Для многослойной стенки коэффициент теплопередачи

К = „ 1------------------- • (2.89)

1/04 + I (SjAj) + 1/«2

I = 1

Величина, обратная /с, называется полным термическим сопротив­лением :

R = 1//С = 1 /ОСі + T (8«Al) +

Рис. 2.9. Распределение температуры по тол­щине однослойной ци­линдрической стенки

Рис. 2.7. Стационарное распределение темпе­ратуры в трехслойной плоской стенке при A, j •< Х-2 <

Рис. 2.8. К выводу уравнения теплопере­дачи через однослой­ную плоскую стенку

І= 1

Температуры поверхностей стенки T'C и T'C в этом случае опре­деляются из уравнений (2.83) — (2.85), а плотность теплового потока — из уравнения теплопередачи (2.86). Температуры на границе слоев опре­деляются как в случае чистой теплопроводности по известным величинам Q и одной из температур слоя.

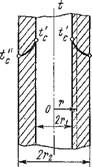
Цилиндрическая стенка. Граничные условия пер­вого рода. Имеется цилиндрическая стенка (труба), длина которой I существенно больше толщины (рис. 2.9). Такой цилиндр называется неограниченным. Обозначим внутренний радиус трубы гь а наружный г2. Теплопроводность материала стенки будем считать постоянной. Изотермические поверхности являются цилиндрическими, имеющими общую с трубой ось, а тепловой поток направлен радиально.

При заданных условиях температура изменяется только в радиаль­ном направлении и температурное поле будет одномерным.

В цилиндрической системе координат дифференциальное уравнение теплопроводности (2.68) при отсутствии внутренних источников теплоты будет:

Дх Sr г дг Dzt 1 Dt

Где + - ~ - оператор Лапласа в цилиндрических координатах.

При стационарном тепловом режиме Dt/Dx = 0 и дифференциальное уравнение теплопроводности (2.90) примет вид

D2t J_JiЈ Dr2 г Dr

Т + = (2.91)

Граничные условия первого рода запишем в виде: при г = гІ T = T'C При Г = г2 T = T'C.

Введем новую переменную и = dt/dr. Подставляя и в (2.91), получим

Уравнение в новых переменных:

+ — du = 0. (2.93)

Du dr ' г

Разделим переменные

D и Dr — + — = 0. И г

После интегрирования получим

1п» + In г = In Сх.

Потенцируя уравнение, получим

И = С І/г. (2.94)

Приравнивая значения и = Dt/Dr и и = С і /г, определяем зависимость температуры от координаты:

Dt/Dr = С І/г и г (г) = Ci In г + С2, (2.95)

Откуда следует, что кривая распределения температур по толщине цилиндрической стенки представляет собой логарифмическую кривую, показанную на рис. 2.9.

Из граничных условий (2.92) определим постоянные интегриро­вания

Cl = - ZlZIL. (2.96)

Ln-^ R I

C2=t'c-Tc~ U In;-,. (2.97)

Подставляя значения Сt и С2 в уравнение (2.95), окончательно получаем выражение для температурного поля:

T (г) = T'C - (T"C - T'C) ■Ln.(R/''L).- (2.98) Щгг/гі)

Количество теплоты, проходящее через цилиндрическую поверх­ность площадью F = 2лт/, найдем из закона Фурье

(2.99)

Градиент температуры Dt/Dr обозначен и и определяется соотно­шением

Dt Сі T'c — T'c , MX,

~T~ — и =■ -- =---- 7-7—7-r-. (2.100)

Dr r rln(r2/ri)

Подставляя значение градиента температуры в уравнение (2.99), получаем

In (г 2 /г і)

Обычно плотность теплового потока относят к единице длины трубы

«-Г-Е&^-'Э - <2102>

Для тонких труб большого диаметра при D2/DІ < 2 можно считать тепловой поток по формулам для плоской стенки (2.80) и (2.81). Ошибка составит меньше 4%.

Для расчета теплового потока Q в цилиндре можно воспользоваться

Формулой для плоской стенки Q = AtcF.

В случае цилиндрической стенки уравнение для Q (2.101) умножим и разделим на толщину стенки, равную А г:

Л 2 л/X, Atc А г

Q —-------------------------------------------------------------------------------- ^

In (г 2/г і) А г

Тогда можно записать

E = ^-ArcFcp, (2.103)

Где 5 = A г = R 2 — гх; Fcp = 2 Nrcpl; Rcp = (R2 — r^/lnO^/ri) — средний радиус цилиндрической стенки. Формула (2.103) аналогична формуле (2.81) для плоской стенки.

Для расчета теплопроводности многослойной цилиндрической стенки воспользуемся той же методикой, что и в случае плоской много­слойной стенки и с теми же ограничениями — контакт между слоями совершенен, теплопроводности слоев Xi постоянны.

Напишем значение линейного теплового потока Qt для каждого из слоев:

2пХ і ,

Qt =————— (ґс — tc, І);

In (r 2 /г X) LnX2 , .

(2.104)

2 кХп

& = Тгйгт.—~

ІП (' n/7 n — i)

Решим уравнения (2.104) относительно разностей температур и сложим. Тогда получим

£ - Ґ' = —in Гі. + _L lniL+... + _Lln

2к у Я-! Rx X2 R2 X„ R„-I

Откуда линейная плотность теплового потока

Л (t'c - tc)

Ql =

1 1 Г2 , 1 , Г3 І Гп

•XT—In-- h -^J— In---- b... + -^r- 111--------

IK I }'i IA2 r2 ZA„ r„-i

Для n-слойной стенки:

(t'c - T'C)

Qi — „ } rt ■ (2.105)

І

I==1 2 кХі I'i-i

Величина * In Г' называется линейным термическим сопротив - 2тсЛ[- г І -1

" 1 г-

Лением отдельного цилиндрического слоя, а величина £ ——'■----

І=12%кі Гі-х

Полным линейным термическим сопротивлением цилиндрической стенки.

Цилиндрическая стенка. Граничные условия третьего рода. Теплопередача. Рассмотрим неограниченную цилиндрическую стенку толщиной 5 = г 2 — г і. Заданы температуры тепло­носителей ti и T2, омывающих поверхности стенки, причем будем считать ti > T2. Заданы коэффициенты теплоотдачи ах и а2 на по­верхностях стенки со стороны горячего и холодного теплоносителей.

Напишем уравнения для линейной плотности теплового потока: Ql = A.1(Tl ~ F'C)7Cri; 2тсХ,

— <*2 (*е — 12) 2-я г 2.

Решаем эти уравнения относительно разностей температур и скла­дываем. Получаем

,1 1 . 1

Tl-T2 = Qt —------------ + —- In — + —-------------

Аі 2ші 2кХ г І A.22Nr2

Откуда

T2) (T1 - T2)

= ' + ' , * + ■ = ~------------------- іТа----------------- <2-><*>

+ - r—r-ln------ h --- 1---- ---------- — + r-T-ln -f - +

Ai2rc Гі 2 NX ri a22rcr2 aiTt dx 2nX dx ct2Ttd2 Обозначим

1

(2.107)

1 ^ 1 1 d> л. 1 + ^г-т-ln — +

Ai nd І 2 тсЛ, Dx a 2nd2

Величину Кі называют линейным коэффициентом теплопередачи. Величина, обратная /сь называется полным термическим сопротив­лением цилиндрической стенки и обозначается R,:

R J_ = + _Lln ^ + = R + R + R (2.108)

/С, Axizdi 2пХ Dx . A2%d2

Где Di и D2 — внутренний и наружный диаметры трубы.

Как и в случае плоской стенки, полное термическое сопротив­ление теплопередачи цилиндрической стенки есть сумма частных термиче-

1 1

Ских сопротивлении JR, 1 = --------- — и Ri 2 = --------- — и термического сопро-

Ajjti/i ' ос2тш2 1 л

Тивлеиия стенки jR/,t

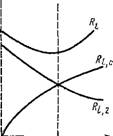
Из формулы (2.106) видно, что при постоянном Di с увеличением D2 увеличивается термическое сопротивление Ri, с, но уменьшается термическое сопротивление теплоотдачи со стороны холодного тепло­носителя Ri, 2. Такая двойного характера зависимость полного терми­ческого сопротивления Ri цилиндрической стенки означает, что сущест­вует значение D2, при котором Rt имеет экстремальное значение. Приравняв первую производную нулю:

DRi _ 1________ 1_ = 0

D (D2) 2Xd2 A2Dl

Найдем

D2 = 2tya2. (2.109)

Так как вторая производная положитель­на, то найденному значению D2 соответству­ет минимальное тепловое сопротивление Ri (рис. 2.10) и согласно (2.106) максимальная плотность теплового потока Qt. Величину Di, Определяемую соотношением (2.109), называ­ют критическим диаметром трубы

DKp = 2Х/а2. (2.110)

Іі

<кр

При увеличении наружного диаметра до DKp тепловые потери цилиндрической стенки растут. Для уменьшения потерь теп­лоты изолированным трубопроводом необ­ходимо, чтобы наружный диаметр изоляции был больше DKp. Это положение следует

Учитывать при выборе материала и тол­щины слоя изоляции трубопроводов.

Условие (2.110) может быть выражено равенством

ВіІф = A2DKp/X — 2. (2. Ill)

Этому значению числа Био соответствует максимальное значение теплового потока. При Bi < 2 увеличение слоя изоляции до DKp ведет к увеличению теплопотерь.

Шаровая стенка. Граничные условия первого рода. Рассмотрим полый шар с радиусами и г2, с постоянной тепло­проводностью материала X и температурами поверхностей T'C и T'I

R, к

Рис. 2.10. К определению критического диаметра цилиндрической стенки

Так как температура изменяется только в радиальном направ­лении, то дифференциальное уравнение теплопроводности в сфери­ческих координатах будет

Dt ~дх

Д~£ 2 Dt - т +-------------

(2.112)

= а

Dr

Г дг

D2T 2 Dt ,

Где —j - 4- — = Vn — оператор Лапласа в сферических координатах.

При стационарном тепловом режиме температура не зависит от времени Dt/Dx = 0 и уравнение (2.112) принимает вид

0.

(2.113)

D2T 2 Dt Dr2 + 7"dT

Граничные условия первого рода:

При г = г і T — T'C,

При г = R2 T = T'C. (2.114)

Дважды интегрируя уравнение теплопроводности (2.113), получаем

А =£}_;»(„ (2.115)

Определим постоянные интегрирования из граничных условий

" ч ' L. tc ^с 1

1 =----- І----- г» L 2 = І с------------ :--------- Z--------- •

1 1 Гі

''і

Подставляя значения постоянных в (2.115), получаем выражение для температурного поля в сферической стенке

П Г2

Из формул (2.115) и (2.116) видно, что температура г (г) изме­няется по формуле гиперболы. Тепловой поток найдем, подставив градиент температуры dr/dr в уравнение закона Фурье при площади изотермической поверхности F = 4лт2:

Q= —— —(г'с — t'c) 4я. (2.117)

Гі r2

При граничных условиях третьего рода уравнение теплопередачи будет

Б-------------------- _ (2.118)

^ 1 1/1 1 1 v '

+ 7?н "ї--------------- г~ i +

Oti^i 2A, d2 J a2d2

Где T%, T2 — температуры теплоносителей; oti и а2 — коэффициенты теплоотдачи на внутренней и наружной поверхностях шара; Du D2 — Диаметры.

Для сферической стенки тепловой поток может быть рассчитан по формуле, аналогичной для расчета теплового потока в плоской стенке. Преобразуем (2.117):

Q = Z ~ п (T'C - t'c) 4тс =

11 R2 — Г у

Г Г2

Обозначая 8 = г2 — гь гср = ]/Rir2 и Fcp — 4кг%, получаем расчетную формулу в виде

Q = ~AtFcp. (2.119)

1 с	— T" 1 с
1	1
Гі	Т2

Уравнение теплопроводности для многослойной сферической стенки может быть получено аналогичным образом, как оно получено для плоской и цилиндрической стенок. Опуская громоздкие выкладки, напишем расчетную формулу в виде

У Г ГТ+ і

- 4n(t'c-t"c)

(2.120)

1 І-І+1
где ГІ и ri+i — меньший и больший радиусы і-го слоя шаровой стенки.

Теплопроводность при наличии внутренних источников теплоты. Про­цессы теплопроводности в химических системах осложняются дей­ствием экзотермических или эндотермических эффектов, при которых теплота выделяется или поглощается во всем реакционном объеме. К этому классу задач относятся также системы с фазовыми превращениями, а также процессы, связанные с индукционным или диэлектрическим нагревом.

При наличии источников теплоты постоянной мощности Qv (Вт/м3) решение задач одномерного температурного поля сводится к решению дифференциального уравнения (2.71):

Опуская громоздкие выкладки, не представляющие собой матема­тической трудности, приведем окончательные результаты решения уравнения (2.121).

Для пластины толщиной 2R при граничных условиях третьего рода а = const и Tx — const при симметричном охлаждении и постоян­ной теплопроводности X решение будет:

+ ^ + (2-123)

Tr = tx + (2.122)

Для цилиндра радиусом R

' 2а АХ

Для шара радиусом R

«г+ + - И). <2Л24>

Общее решение задачи одномерного температурного поля в крите­риальной форме может быть записано в следующем виде:

= — Pof 1 - (2.125)

Tx п V R Bl /

Где Ро = (QvR2)/(Xtx) - критерий Померанцева; Bi = (осR)/X - критерий Био; п — постоянное число: для пластины п = 2, для цилиндра П = 4, для шара п = 6.

При Bi оо граничные условия третьего рода вырождаются в гра­ничные условия первого рода Tc = Tx = const. В этом случае общее решение будет:

Или

Tr = To + — ^-(R2 - Г2). (2.127)

Її Л»

Уравнение (2.127) показывает, что распределение температуры в пластине, цилиндре и шаре при наличии равномерно распреде­ленных внутренних источников теплоты постоянной мощности под­чиняется параболическому закону.

Как следует из уравнения (2.127), мощность внутренних источников теплоты может быть определена по разности температур на поверх­ности тела и любой точки тела At = tr — tc:

ПХ At

Qv — {ілі 5)

При г = О температура в центре равна tu. В этом случае величина (QvR2)/(NX) имеет смысл полного перепада температур в теле:

,Ц_,С = М1 (2.129)

Мощность внутренних источников в этом случае может быть оп­ределена из соотношения

ПХ Я3

(2ЛЗ°)

Которое для пластины, например, имеет вид

IX

Qv = jr(tn~tc). (2.131)

Нестационарная теплопроводность. В химической технологии не­стационарная теплопроводность связана с прогревом или охлаждением материала и оборудования при запуске, остановке или изменении технологического режима процесса. Особый интерес представляет анализ нестационарной теплопроводности в тех случаях, когда химический процесс сопровождается экзотермическим или эндотермическим эф­фектом. В этом случае расчет теплопроводности с учетом внут­ренних источников теплоты позволяет получить важные кинетические и термодинамические характеристики химического процесса.

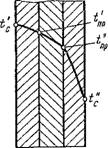
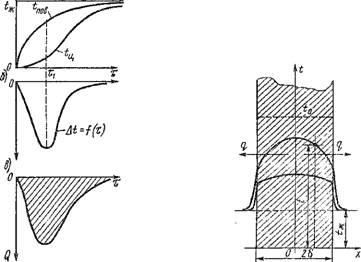
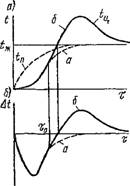
На рис. 2.11, а показаны кривые изменения температуры тела в процессе его нагревания. При погружении тела в среду теплоносителя с постоянной температурой t, к сначала прогревается поверхность тела t„, а спустя какое-то время начинает изменяться температура центра Гц. С увеличением времени прогрева температуры в теле выравни­ваются и при х -» оо становятся равными температуре греющей жид­кости. Иа рис. 2.11,6 показана дифференциальная термограмма этого процесса At = F (х), где At = T„ — t„. Максимальная разность температур поверхности и центра соответствует времени ть а затем уменьшается и при х -»оо стремится к нулю, когда тело полностью прогрето. Характер изменения теплового потока, поступающего в тело при его нагревании, показан на рис. 2.11, е. В начале процесса прогрева Q Велико, а затем уменьшается. Площадь, ограниченная осью абсцисс и кривой Q = F (х), соответствует полному количеству теплоты, поступив­шему в тело за время х. Теплота Q идет на повышение энтальпии тела.

Рассмотрим некоторые простейшие задачи нестационарной тепло­проводности. На этих примерах рассмотрим физические особенности процессов, методы решения задач нестационарной теплопроводности, а также возможности практического использования полученных ре­шений.

Аналитическое описание процесса включает в себя дифференциаль­ное уравнение теплопроводности и условия однозначности. Для одно­мерных тел дифференциальное уравнение теплопроводности может быть представлено в следующем виде [см. уравнение (2.79)]:

(2.132)

Где г — текущая координата; Г — постоянное число: для пластины Г = 0 (г — х), для цилиндра Г = 1 (г = г); для шара Г — 2 (г = г).

Количество теплоты Qv, выделенное в единице объема за единицу времени, может быть в первом приближении принято постоянным и равномерно распределенным, как в электронагревательных элементах, или зависящим от времени, как в химических процессах.

При отсутствии внутренних источников теплоты уравнение упро-

Щается:

(2.133)

Физические параметры тела А., с, р будем считать постоянными, а началь­ное распределение температуры равно­мерным.

T Рис. 2.11. Термограм­мы прогрева образца: простые (д); дифферен­циальные (б); теплота, затраченная на про-

Рис. 2.12. Распределение температуры в неогра­ниченной пластине при нестационарной тепло­проводности

Грев образца (в)

Решение задачи нестационарной теплопроводности сводится к опре­делению зависимости температуры и переданного количества теплоты от времени для любой точки тела.

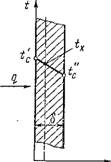
Охлаждение (нагревание) пластин ы. Г р а н и ч н ы е условия третьего рода. Дана неограниченная пластина тол­щиной 28 (рис. 2.12). В начальный момент времени (х = 0) темпе­ратура в пластине распределена равномерно и равна TQ. Пластина помещена в среду с постоянной температурой f, K < T0. Теплообмен на обеих поверхностях пластины происходит при постоянных коэффи­циентах теплоотдачи а = const. Требуется найти распределение темпе­ратуры в пластине T = T (х, т).

При поставленных условиях распределение температуры по тол­щине пластины должно быть симметричным Dt (0, х)Jdx = 0, а искомая функция T (х, т) должна быть четной функцией координаты х. Пластина сделана из однородного и изотропного материала с постоянными теплофизическими характеристиками.

Математическую формулировку задачи можно упростить, если ввести избыточную температуру Ф = T — Іж. Тогда дифференциальное уравнение теплопроводности (2.133) для пластины при Г — 0 можно записать

(2.134)

Краевые условия:

TOC o "1-3" h z начальные условия при т = 0 3(х, 0) = (а)

~ f д§ ос А

Граничные условия при х = 8 1—1 = —— (б)

ох/х=й А.

Условие симметрии при х = 0 (ІІ-) = 0. (в)

ох/х=0

Найдем функцию 3(х, т) распределения температуры в пластине в любой момент времени процесса охлаждения (нагревания). С этой целью используем простой и достаточно универсальный метод раз­деления переменных. Будем искать решение уравнения (2.134) в виде произведения двух функций, одна из которых <р(х) зависит только от пространственной координаты, другая/(х) зависит только от времени:

S(x, х) = Ф(х)/(х). (2.135)

Подставляя выражение для 9 в уравнение теплопроводности (2.134) и разделяя переменные, получим

1 дЦ{<0„д 1 д2[ф(*)]

/ (х) дх ф(х) дх2

Левая часть этого уравнения зависит только от х, а правая — только от х. Известно, что две функции от двух разных и не зависящих друг от друга аргументов могут быть равны при любых значениях последних только в том случае, если они постоянны. Величина эта является отрицательной и обозначается к2. Тогда получим два дифференциальных уравнения:

<*[■/»] = „ак2. (2Л36) /(т) dx ' к '

ІІ^І + /с2ср(х) = 0. (2.137)

Dx

Уравнение (2.136) решается разделением переменных

-аЄб,

/М

После интегрирования этого уравнения получим In [/(х)] = —ах/с2 4- In Сі и общее решение будет

/(х) = Сле~ак2 (2.138)

Из уравнения (2.138) видно, что знак постоянной величины к2 Выбран правильно, так как при значении х оо температурная функция F{X)-*- 0, что соответствует физическому смыслу. В противоположном случае, при положительном значении к2 при х->оо, /(х)-> оо, т. е. приводит к нереальному результату. Общее решение (2.137) имеет вид

Ф (х) = С2 COS (Кх) + С З sin Ikx). (2.139)

Подставляя выражения ф(х) и / (х) в уравнение (2.135), получим

& = [С2 cos (кх) + С3 sin(/<x)]

Или, обозначая CiC2 = С и CiC3 = D:

& = [Сcos ikx) + Dsin(/cx)] e~akh.

Постоянные С, D и к определяются из начальных и граничных условий (а), (б), (в). Постоянная D определяется из условий сим­метрии (в):

( - fa] = Ск sin кх + Dk cos (кх)] е "ак (2.140)

Так как к Ф 0 (стенка охлаждается или нагревается), к cos (кх) ф 0 при х = 0, то постоянная D должна быть равна нулю. Таким образом,

$ = cos (be). (2.141)

Собственные значения к = к„ найдем, используя граничные условия (б). На левой поверхности пластины х= —5; подставляя в (б) решение (2.140) и (2.141), получим

Ске~ак'х Sin(/C5) = -^Ce~Ak2'Cos(Kb),

A

Или, сокращая, получим

Ctg(/c5) = (кХ)/а.

Умножив числитель и знаменатель на 6, получим

, ,, ~ч /с8 /с8 , ,

ВГ (2Л42)

Введем обозначением р = /с8 и тогда

Ctg (j-i) = ji/Bi. (2.143)

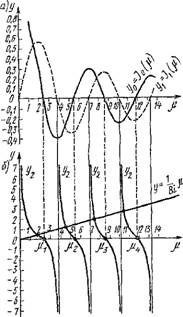
Из анализа характеристического трансцендентного уравнения (2.143) видно, что р. имеет бесчисленное множество значений. Уравнение (2.143) наиболее просто решается графическим путем (рис. 2.13). Обозначим ctgn = yb a j-i/Bi = у2 и построим графики этих функций. Первый график представляет собой котангенсоиду, являющуюся перио­дической функцией аргумента р. с периодом тс. Второй график — прямую, тангенс угла наклона которой к абсциссе равен 1/ВІ. Абсциссы точек пересечения этих графиков дают значения корней р уравнения (2.143).

Как видно из рис. 2.13, уравнение (2.143) имеет бесчисленное множество корней р.,, (п = 1, 2, 3,...), удовлетворяющих уравнению (2.134) и граничному условию (б). Из уравнения (2.143) следует также, что значения щ, которые называются собственными числами, зависят от порядкового номера п и числа Био.

При Ві = 0 прямая у2 — р/Ві совпадает с осью ординат, тогда Ці = 0; х2 = 7с;... ;ц„ = (п — 1)тс.

При Ві со прямая у2 = м/Ві совпадает с осью абсцисс, тогда корни уравнения (2.143) будут равны щ = тг/2, р2 = Зтс/2,..., р„ = (2п - 1) тс/2.

Для других значений критерия Ві первые три корня характе­ристического уравнения (2.143) приведены ниже:

Ві.............................. 0 0,01 0,1 1,0 10 80 100 оо

Ці............................. 0,000 0,0998 0,3111 0,8603 1,4289 1,5514 1,5552 1,5708

i2.............................. 3,1416 3,1448 3,1731 3,4256 4,3058 4,6543 4,6658 4,7124

Цз............................. 6,2832 6,2848 6,2991 6,4373 7,2281 7,7573 7,7764 7,8540

Метод разделения переменных позволяет получить совокупность частных решений удовлетво­ряющих дифференциальному урав­нению теплопроводности и гра­ничным условиям. Каждому значе­нию корня цп соответствует част­ное распределение температуры. Сумма частных решений являет­ся общим решением уравнения теплопроводности

(2.144)

И		%		У1		Уі
						Jh^
				| А
Л4		Л		А	Ш	І

Рис. 2.13. Графический способ оп­ределения корней характеристи­ческого уравнения

Значения констант С„ опреде­
ляются из начальных условий. При Fo = О (т = 0) получаем

Э0 = 3(х,0)= £ (2.145)

Воспользуемся свойством ортогональности тригонометрической функ­ции. Для этого (2.145) умножим на cos(pmx) и проинтегрируем в пределах — 8 ^ х < 8:

5 °° 5

M!5CosDx = YJ С„f _. cos(ршх)cos(рп.) dx.

N= 1 6

Свойство ортогональности в нашем случае может быть записано

В виде

F_ 5 cos (№nx) cos сЬс = | s cos2 (ЦпХ) d х (2.146)

Для т = п интеграл (2.146) равен

.а

2/.. , 5Ш2ЦП

Cos ( dx = 5 1+ —— _s 5 У 2Ц„

И C„ из (2.145) получает вид

Зо cos pn| dx во —sin p„ І _, J - & J _ Pn

Sin 2pn ji„ + sin |in cos p„ +

Ii oin 11 <->ло 11 '

J8 cos^ti.-ijd^ «(l

2|X„

-5 " / -

Подставив найденные значения C„ в уравнение (2.144), получим окончательное решение для симметрично охлаждаемой однородной пластины

У Оо----------------------- cos L4V ^ (2.148)

Li + sinp(icos|in V 5/

Я= 1

Или в безразмерной форме

П=1

Где А„ = 2 sin |V(|i„ + sin ри cos р„).

Решение (2.149) действительно и для случая прогревания пластины,

Только необходимо положить

А _ І q „ t(x, Х) - to

Онагр — 1 ~ "охл —

Іж T0

Так как cos (ц„х/8) — величина ограниченная, а ехр( — |A2Fo)-- Величина быстро убывающая, то, как показывает анализ уравнения
(2.149), при Fo 0,25 ряд становится быстро сходящимся и может быть заменен с достаточной точностью первым членом.

В этом случае распределение температуры в пластине может быть получено из уравнения

Є = А і cos^|ii-^exp(-n? Fo). (2.150)

Область вырождения функции (2.149) в (2.150) называют регулярным тепловым режимом.

При заданных координатах х искомая температура 9 есть функция только критериев Ві и Fo:

О = /(Bi, Fo). (2.151)

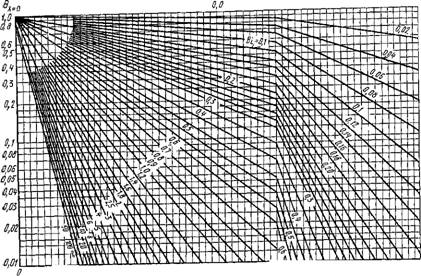
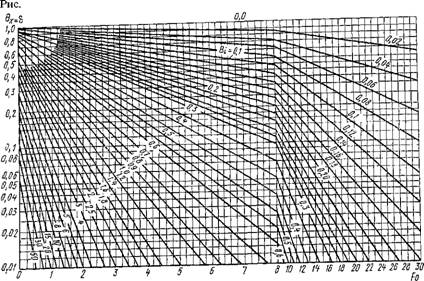
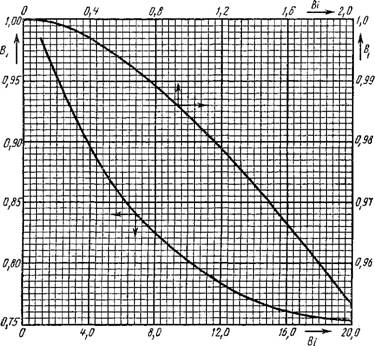
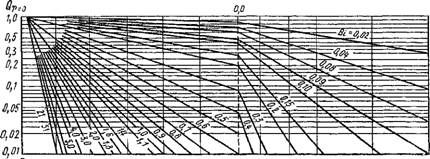
Для практических расчетов температуры в центре и на поверхности пластины обычно пользуются номограммами, приведенными на рис. 2.14 и 2.15. Пользуясь номограммами, можно:

Определить время охлаждения Fo == (ах)/В2 (нагревания) до заданной температуры 0Х=Й или 0Л=О по известным условиям теплоотдачи на поверхностях;

Определить температуру через заданное время;

Определить интенсивность теплоотдачи на поверхностях при заданных Fo и 0.

При Ві -+ оо температура поверхности пластины становится равной температуре охлаждающей (нагревающей) среды, граничные условия третьего рода переходят в граничные условия первого рода. Как показывают расчеты, таким свойством обладает поле при Ві ^ 100. Тогда р„ = (2п - 1) тс/2 и коэффициент А„ в уравнении (2.149) равен

При п = 1 А і = 4/тг, при п = 2 А2 = — 4/(Зя),— Если ограничиться первым членом, то безразмерная температура оси пластины

4

,Fo - к2/*

— е Тс

Решая относительно времени, получим

452 1 , ( 1 4 Х = —5 M

0* = О Я

Безразмерная температура поверхности 0x=<i = 0. При Ві -»■ 0, когда внутреннее термическое сопротивление мало по сравнению с термическим сопротивлением на поверхности, температуры по толщине пластины распределяются равномерно. Как следует из характеристического уравнения (2.142), х„ = (п— 1) тс, а величина

. .. 2sinp„

Ап = Urn----------- :---- —------

|.іи + sm ц„ cos p. n

Принимает значения: Лі = 1, Аг — А3 = ... = А„ = 0. Безразмерная температура находится

Безразмерные температуры поверхности и оси пластины практи­чески равны:

0х=о = e~BiFo; ex=(, = cos]/Bi

1 - 2 J 4 S В 7 8 Ю 12 № № IS 20 22 2* 26 28 50 FО 2.14. График для расчета температуры в средней плоскости пластины

Рис. 2.15. График для расчета температуры поверхности пластины

Определение расхода теплоты на охлаждение (нагревание) пластины проводится в такой последовательности. Находим изменение энтальпии единицы объема материала стенки за произвольный промежуток времени

Q = скр (9„ - 9). (2.153)

Подставляя вместо 90 и & их значения, получим

(2.154)

Q = ср [T0 - TK)(L - —j = ср (f0 - Гж)(1 - 8).

Средняя по толщине пластины температура 9 в соответствии с теоремой о среднем может быть определена по формуле

9

(2.155)

9(х, т) dx.

Подставив в формулу (2.155) значение 0 из уравнения (2.149), получим

9

9

Cos ( у ) ехр (- p2Fo) dx

Н= I

_9о

Ап ехр (- р2 Fo)

Cos ( |i„ - g-1 dx =

Ii= і

. . 2 Г Ssin|.ln X /2.

A„ exp (— p2 Fo) ------------- Q 4 °

9o X

90 > Bn exp ( p,, Fo). (2.156)

F/i

(2.157)

В

Средняя относительная температура пластины 9

X B„exp(-p2Fo),

Э-о

Где

S111 р„ Ри

В„ = А„

2ВІ

Р2 (Ві2 + Ві + ц„)

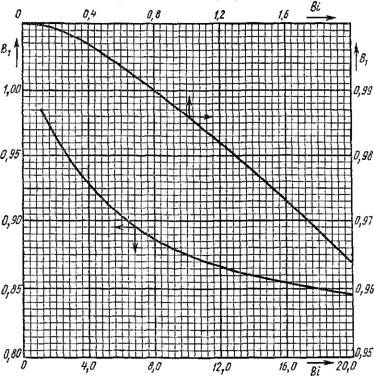
Как видно из уравнения (2.157), величина 6 зависит лишь от чисел подобия Fo и Ві. Ряд (2.157) быстро сходится и при Fo 0,25 можно ограничиться первым членом ряда:

Величина Bj

0 = Вів-мїго. (2.158)

2Bi

Зависит только от критерия Био

Р! (Ві2 + ВІ + ц?)

И для ее определения удобно пользоваться графиком, приведенным на рис. 2.16.

Рис. 2.16. Зависимость Вх =/(Ві) для уравнения (2.158)

Рис. 2.17. Графический способ оп­ределения корней характеристи­ческого уравнения

Охлаждение (нагревание) цилиндра. Граничные условия третьего рода. Рассмотрим бесконечно длинный цилиндр радиусом г0, охлаждаемый через боковую поверхность в среде с постоянной температурой гж. Коэффициент теплоотдачи остается постоянным в течение всего процесса охлаждения. Требуется найти распределение температуры в цилиндре T (г, т) и плотность теплового потока.

Дифференциальное уравнение теплопроводности в цилиндрической системе координат (2.133) при Г = 1 будет

Dt _ / D2T L_<H дх I дг2 г дг

«ЬІГЗ - + - ТГ). (2159)

Как и в предыдущем случае, введем новую переменную & = T — T* и уравнение теплопроводности перепишем в виде

Д& / д2& 1 д&

W=a{wr+Tir} (2М0)

Начальное условие при т = 0 = const (а)

Граничные условия:

Г О

Задача, как и для неограниченной пластины, может быть решена методом разделения переменных. Приведем окончательное решение в безразмерной форме:

Оо 1-д

»=' n=1 (2.161) где R = RjrО - безразмерный радиус, который изменяется в пределах J0 (р„), Jo (h„JR), J і (|л.„) — функции Бесселя первого рода нулевого и первого порядков.

Характеристические числа являются корнями трансцендентного уравнения

Іо(ц)АМ|і) = [і/ВІ. (2.162)

На рис. 2.17 представлен вид функций у0 = Jo (і-О и yi = J І (ц), а также графический способ решения уравнения (2.162). График функции у2 = Jo(i)/Ji (ц) напоминает когангенсоиду с убывающим периодом, а график функции у = p/Bi — прямую линию, проходящую через начало координат. Первые три корня уравнения (2.162):

В і.................................. 0,0 0,01 0,10 1,0 10,0 80,0 100,0 оо

Ц,................................... 0,000 0,1412 0,4417 1,2558 2,1795 2,3750 2,3809 2,4048

Ц2................................... 3,8317 3,8343 3,8577 4,0795 5,0332 5,4516 5,4652 5,5201

Из.................................. 7,0156 7,0170 7,0298 7,1558 7,9562 8,5466 8,5678 8,6537

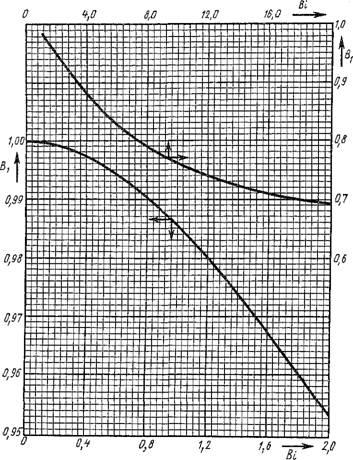
Все принципиальные выводы о влиянии критерия Ві на температур­ное поле, сделанные для неограниченной пластины, остаются в силе и для бесконечного цилиндра. При Fo 5s 0,25 ряд (2.161) быстро схо­дится и для практических расчетов можно ограничиться учетом первого члена ряда. Тогда для расчета температуры на поверх­ности цилиндра можно использовать формулу

0r = Ro = At Jo (pi R) = No (Ві) е-и'Ч (2.163)

Для оси цилиндра

Єг = о = Atf-Rt*0 = MQ (Ві) exp (— p? Fo). (2.164)

Величины 6,. = Го и 0r = o являются функциями только чисел подобия

Tv се о „ At _

= и Ьо==~т- Для их определения по уравнениям (2.163)

К V о

И (2.164) пользуются графиками, приведенными на рис. 2.18 и 2.19. Изменение энтальпии тела за время т определяется формулой

Q = cp(&o-§). (2.165)

Средняя относительная температура цилиндра определяется по формуле

-A-f »2тсгёг. (2.166)

7СГ ® '

Подставив значения Э из (2.161), после интегрирования получим 00 00 У 4J?(HJ , V 4ВІ. ,„ ,

« = 1 —1 (2.167)

При Fo ^ 0,25 воспользуемся первым членом ряда (2.167), тогда

S= Ц?^ТвР)ехр<-цгро)' (2Л68)

Предэкспоненту, зависящую только от Ві, можно определить графически, как показано на рис. 2.20:

4ВІ

Вх =

P?(l4 + Bi2)

Охлаждение (нагревание) шара. Граничные условия третьего рода. Математическая формулировка задачи охлаждения шара радиусом г состоит в следующем. Дифференциальное уравнение теплопроводности шара в сферических координатах запишется

Аа ^ 2 аэ

Дх дг2 г дг

+ ____. (2.169)

VI иг

Начальные условия

9 = = T0 — Tx при х = 0. (а)

Граничные условия:

Рис. 2.19. Безразмерная температура на поверхности неограниченного цилиндра 153

0.95

Рис. 2.20. Зависимость между коэффициентом BL и критерием Ві. для неограниченного цилиндра

Решая совместно уравнение (2.169) с краевыми условиями, получим безразмерную температуру в виде следующей зависимости:

У 2(sinЦ„ - [i„CQS{i„)sin([inR)

П= 1

Где R — R/R0.

Постоянные ри определяются как корни характеристического урав­нения

Tg|.i = - рДВІ - 1). (2.171)

При Fo ^ 0,25 для 0 в уравнении (2.170) можно воспользоваться первым членом ряда

(2.170)

6 = 9 _ 2(Sin Ці - Cos |Ii)Sin(Ni.R) u? Fo _ (ці — sinjii cospOpijR

(2.172)

Ці R

2Bi |/pf — (Bi — I)2 sinjitH ,Fo

HI + Bi2 - Bi

Для определения температуры в центре или на поверхности шара можно использовать графики, приведенные на рис. 2.21 и 2.22.

1 2 3 5" 10 15 20 Fo Рис. 2.21. Безразмерная температура в центре шара

По аналогии с пластиной и цилиндром средняя температура определяется из уравнения

3

(2.173) (2.174) (2.175)

3

-з ■ Г Or2 dr. Г3 J0

Подставляя 0 из соотношения (2.172), полумаем 0 = ВіЄхр(-ц? Ві),

Где

6ВІ

Вг

|х?(ц? + ВІ2-ВГ

Величина Bi может быть определена по графику, приведенному на рис. 2.23. Расход теплоты определяется, как и в предыдущих примерах, по формуле

Q = Ср (Э0 - &). (2.176)

Рис. 2.22. Безразмерная температура на поверхности шара

Рис. 2.23. Зависимость между коэффициентом Bt и критерием Ві Для шара

Нестационарная теплопроводность с учетом внутренних источников теплоты. Термография. Дифференциальное уравнение теплопроводности для одномерного температурного поля с учетом равномерно рас­пределенных в теле внутренних источников теплоты постоянной мощ­ности Qv (Вт/м3) может быть записано в общем виде, как и в предыдущих задачах:

Dt ( Dzt Г Dt Q0

— = а —2-+—-х - + —. (2.177)

Ox or* Г or J Ср

Решение неоднородных дифференциальных уравнений типа (2.177) методом разделения переменных оказывается малоэффективным. Реше­ние может быть получено проще: методом интегрального преоб­разования (операционным методом), например методом интегрального

Преобразования Лапласа. Операционные методы имеют ряд преимуществ перед классическими методами. Метод стандартен и позволяет получать решения в удобном для анализа виде — при малых и больших значениях Fo.

Интегральное преобразование Лапласа определяется формулой

Ь[/(х)]=./і(5) = Jov(T)E-«Dt,

Где/(т) — функция, аД(і) называется изображением функции и обозна­чается обычно в виде L[/(T)].

Решение задач теплопроводности методом преобразования Лапласа существенно упрощается благодаря наличию таблиц изображений. В результате преобразования решать приходится обыкновенное алгебраи­ческое уравнение, после решения которого применяют обратное преобразование (по таблицам), являющееся решением исходного диф­ференциального уравнения. Широкое использование операционного ме­тода при решении самых разных задач теплопроводности нашло в ра­боте «Теория теплопроводности» А. В. Лыкова (М., 1967).

Приведем результаты решения некоторых несложных задач.

Неограниченная пластина толщиной 25 с начальной температурой To нагревается в среде с постоянной температурой? ж. Внутри пластины действует источник теплоты постоянной мощности Q0. Найти распре­деление температуры по толщине пластины.

Математическая формулировка задачи может быть записана при Г = 0 и г = х:

_ дЧ дх дх:

Начальное условие

О (х, 0) = :

Граничные условия:

Дх Д& (0, т) Дх

Решение задачи в безразмерных і

О ^ =3LZ_L = _Lr

"о ~ 2

Оо

- Я1+ilbcos

П= 1

Где Ро = _ ^—- - критерий Померанцева.

К (t>k — to)

+ - к.. (2.178) 1 ср = fac — to- (а) . - 9) = 0; (б) - = 0. (в)

Зеличинах будет Х2 2 >0(1~Ж+ ВЇ

Tvf -) ехР (- l^n Fo), (2.179)

При отсутствии источников теплоты Q = 0 решение (2.179) превра­щается в полученное выше решение задачи [формула (2.149)]. Посто­янные р„ и А„ сохраняют значения в решении (2.149) и равны соот-

1 „ Л З ТРо Г+ш

Ро

Ветствєнно

Рис. 2.24. Простые и диф­ференциальные термо­граммы прогрева образца при отсутствии внутрен­них источников теплоты (а) и с внутренними источ­никами теплоты (б)

2 sin |л„

Ни

А,,

Ctg |І„

ВІ . + Sin |0.„ COS Средняя температура пластины:

00 I

N= 1

Особый интерес представляют задачи не­стационарной теплопроводности для систем, в которых протекают химические процессы. В этом случае мощность внутренних источ­ников теплоты не остается постоянной, а связана с кинетикой самого химического процесса.

1+ )в„ехр(-й„2Ро). (2.І80) М-»

На рис. 2.24, а показано изменение температуры на поверхности Tu И в центре Tu пластины, нагреваемой в среде с постоянной темпера­турой TK — при отсутствии Q (пунктирные) и при наличии внутренних источников теплоты переменной мощности Qv{Т). Если в системе про­текает экзотермическая реакция, то начиная с момента времени т0 температура в центре пластины будет превышать температуру поверх­ности. Температуры будут сближаться, когда химический процесс будет затухать и асимптотически стремиться к ґж, когда реакция закончится. На рис. 2.24,6 показаны зависимости At = T„ — гц = F(X) для инертного материала пластины при простом прогреве (кривая а) и при наличии реакции с экзотермическим эффектом (кривая б). Кривые At = F(X) Называются дифференциальными термограммами.

В химическом процессе выделяющееся количество теплоты пропор­ционально количеству прореагировавшего вещества. Степень превраще­ния вещества может быть выражена соотношением

А = CJCq = AHJAH, (2.181)

Где С, и С0 - концентрации исходного соединения к моменту X и в начале реакции; ДЯТ, АН — количество теплоты, выделенное (поглощен­ное) к моменту т реакции, и тепловой эффект реакции.

Уравнение кинетики химической реакции n-го порядка часто записы­вается в виде

06 = 1

-кх"

(2.182)

Где к — константа скорости реакции; и = є + і - эффективный порядок реакции; т — время реакции.

Количество теплоты, выделяющееся за интервал времени реакции т, может быть определено из соотношения

АН, = FQ Qv Dx (2.183)

И согласно (2.183)

D(ЛЯТ) d r А „,, , І(И

(Jv = _L_lL = [AH(1 - «г" )]. (2.184)

Дифференцируя (2.184), получаем выражение мощности внутренних источников теплоты qv от времени в виде экспоненциальной зави­симости

Qv = qov'e-k'", (2.385)

Где (J0 = к (є 4- 1) АН — величина, постоянная для данной химической реакции, равная произведению константы скорости реакции, теплового эффекта реакции и п = є + 1 — величины эффективного порядка реакции.

Дифференциальное уравнение теплопроводности для пластины с учетом (2.185) имеет вид

Д2& Q0E А---------- 1_ — Дх2 ср

Аэ eg» + ат

Дх дх* ср

Для реакции первого порядка п = 1 и є = 0. В этом случае урав­нение теплопроводности будет

ДВ - -~кх

~дх

(2.187)

Где QQ = к АН.

Решение уравнения (2.187) для неограниченной пластины, имеющей начальную температуру гж, полученное методом интегрального преоб­разования Лапласа, имеет следующий вид:

(2.188)

T (х, х) - T,

E-Fo(kt - й») _ 1

Її—І

Кинетическое число; А,

KR'<

2 sin |хи Jl„ + sin |i„ cos p„

Где Kt

Ц„ - корни

Уравнения ctg цп

В _Нгl Bi '

Для центра пластины х = 0 уравнение после некоторых преобразо­ваний может быть представлено в форме

AHKt Vу А Ег_

Ср

KtFo

> -

(2.189)

Гц T-Й

Р„ — Kt

П = 1

АН

Выразим безразмерной

Ср "" A tHC

Atun а отношение

Обозначим

Температурой 0 (0, т). Тогда уравнение (2.189) примет вид
.-WFo

9(0, x) =Kt2^"

(2.191)

N= 1

Ряд (2.190) быстро сходящийся и для расчета 0(0, х) при Fo ^ 0,25 с достаточной точностью можно воспользоваться первым членом ряда. В этом случае

GKtFo _ g-nfFo

Kt

Ці

Ах

0 (0, х) = Kt

2sin

Где Ax = -

Ці + sin Pi cos Ці

Как видно из уравнения (2.191), температура в химических системах зависит не только от чисел Fo и Ві, но также и кинетических характе­ристик химического процесса. При Ві -> оо температура поверхности пластины становится практически равной температуре греющей среды и тогда решение уравнения (2.187) в форме At = t„ - f„ =/(т) будет уравнением дифференциальной термограммы (рис. 2.24, кривая б).

На анализе термограмм основаны количественные методы термо­графии — определение термодинамических и кинетических характерис­тик химических процессов и фазовых переходов: теплового эффекта, мощности внутренних источников теплоты, констант скоростей эффек­тивного порядка реакции и пр.

В самом деле, вернемся еще раз к дифференциальному уравнению тепло­проводности с внутренними источниками теплоты:

-KtFo

(2.190)

Kt

Ц«

LL-allL+ Jk.

Дх дх2 ср

Решим уравнение относительно Qv:

D2T Дх2

Qv = ср

(2.192)

Из уравнения (2.192) видно, что мощность внутренних источников теплоты может быть выражена алгебраической суммой аккумулирований теплоты и теп­лоты, переданной теплопроводностью [см. уравнение (2.20)]:

<г» = 9ак + Ял - (2.193)

При параболическом распределении температуры по толщине пластины T (х, х) = T (0, т) + Дг (х/Ь)2 среднюю температуру можно выразить

>5

(2.194)

^ср —

Т

T Dx = T (0, т)

Где At — T (0, х) — T (5, т) = ґц — Tn — температурный перепад в центром и поверхностью.

В этом случае Qx будет равно

Пластине между (2.195)

D2lt(0,T)-At(±)2

Qx = -I-L—_ vs;,,^,.

21

Дх2

Мощность внутренних источников теплоты выразится:

Dte p 2 A.

Qv = cp +

От 8J

(2.196)

Вернемся к уравнению (2.188) для центра пластины в форме:

Go ср

-H,;Fo

(2.197)

Е~кх + p2Fo~

Дt = Іц - tn =

2 " » Нл ~ k

Вынесем Xe~Kr и 1/Fo за знак суммы, тогда получим

^-YA,, CPFo i_j

,K. tFo - ^Fo _ і Kt - xl

.(Kt - и») Fo _ 1

,(2.198)

H ~ Tn

-k L І

Kt - p„

Откуда

(2.199)

_2X 4 и — — tn)

Y

E(Kt - Цп)Го _ I

Л»

Lj Kt- tf

N-1

Ограничиваясь первым членом ряда, получим

2Х

At

(2.200)

1

E(Kt - ці) Fo _ j

2/1,

Сравнивая формулу (2.195) и аналитическое решение уравнения теплопро­водности (2.200), можно сделать заключение, что выражение в скобках (2.200) отражает влияние слагаемого Q.DK в (2.193). Значение величины QllK существенно только при расчете кинетики тепловыделений, но может не учитываться при расчете теплового эффекта реакции. В самом деле, тепловой эффект химиче­ской реакции может быть рассчитан интегрированием по формуле

- АН = fT"^dx = ^(i:n-xo),

(2.201)

Цсум

(2.202)

Где т0 и х„ — начальное и конечное время химического процесса. Подставим значение Qu (2.193) в формулу (2.201) и получим

4сум = П" (Q-лк + Qx) = Г" Qm dx + Г" Q% dx = ср (*cp

Где и fЈP — средние температуры образца в начале и конце химической реакции.

При постоянной температуре греющей среды (термостата) обе они равны tiK. В этом случае JT" дак равен нулю и тепловой эффект реакции может быть рассчитан через Q-K по данным термографирования:

2Х Б2

At dx = 1 At dx, 5 Jo

(2.203)

<?сум

Где т — продолжительность химического процесса.

161

Как видно из формулы (2.203), интеграл|т At dx представляет собой пло­щадь, ограниченную дифференциальной термограммой Дг =/(х) и осью абсцисс х. Эту площадь можно выразить F = Atcpx, тогда тепловой эффект будет равен

6 А. В. Чечеткин, 1-І. А. Занемонец

T

U

Рис. 2.25. К расчету тепловых эффектов реакции методом тер­мографических балансов

Рис. 2.26. Кинетическая кри­вая, полученная методом тер­мографических балансов

АН — Qc— -§-Дґсрт = (2-204)

F

Где Atcр = (£„ - Rn)Cp = — .

По данным термографирования может быть рассчитана кинетика тепло­выделений (теплопоглощений) qv =/(х) и глубина протекания химического про­цесса а (2.181) по формуле

А " 4тГ = С dTHio dx>- (2.205)

ZA, . >.

Подставляя Q0 = —r-At и считая теплопроводность л постоянной, получим 5г

А = (JJ At dx)/(JJ Ar dx) = F/F, (2.206)

Где / — площадь, ограниченная дифференциальной термограммой от начала реакции х = 0 до любого расчетного времени т(; F — вся площадь под диффе­ренциальной термограммой (рис. 2.25).

Кривая а =/(х) (рис. 2.26) представляет собой обычную кинетическую кри­вую химического процесса, рассчитанную, как было показано выше, с исполь­зованием методов нестационарной теплопроводности. Константа скорости реак­ции, температурный коэффициент и энергия активации по полученным данным а могут быть рассчитаны обычным путем из уравнения (2.182) и уравнения Аррениуса.

Количественное определение термодинамических и кинетических параметров химического процесса по результатам расчета температурного поля в виде At = /(т) и составляет содержание количественных методов термографии.

Охлаждение (нагревание) тел конечных размеров. В теории тепло­проводности задачи на охлаждение (нагревание) тел конечных размеров решаются в соответствии с теоремой о перемножении решений. Суть теоремы состоит в том, что если есть решения уравнений теплопро­водности для двух неограниченных пластин

Dt(x, Х) =д 82t(x,x) . Dt(y,x) _ а D2t (.у, х) Дх дх2 ' дх ду2 '

То температура T(Xyx) в любой точке оси симметрии неограниченного
прямоугольного стержня определяется в соответствии с теоремой о пе­ремножении решений как произведение двух функций:

T (лут) = I (хт) • I(Ух). (2.207)

Для доказательства этого положения напишем дифференциальное уравнение теплопроводности для двухмерного поля неограниченного прямоугольного стержня:

Dt (луг) ( D2T D2T

Дифференцируя уравнение (2.207) по х, у и х, получим: D2T{Xyx) / ч Dzt (хт)

TOC o "1-3" h z —= H>'t) ; (а)

Их ОХ

^(хух) d2t(yx) .

—ї—.f(xТ)-^-, (б)

Dt (хуг) & (хт) . . dt (ух)

Подставляя производные по т из дифференциальных уравнений для неограниченной пластины

Dt(xx) d2t (хт) dt(yx) d2t(yx) — ---■ = а ———-=.— и — = а

Дх дх дх ду~

получим

Дх

Dt (хут)

W , D2T (хт) , . D2T (ух) T(.V, т) а12 + T(X, х)

Дх2 ' V ' ' ду2

Подставляя выражения (а), (б), (в) в дифференциальное уравнение (2.208), получим тождество

Ч D2T(Xx) , ^d2t{yx)l Г ^d2t(xx) . чд2фт)1

T {yx) t (XT) = Fl * Іл) -Jjr- + T M -^-J>

Что и требовалось доказать.

Если рассматривать параллелепипед как тело, образованное пересе­чением трех неограниченных пластин, то безразмерная температура в точке с координатами х, у, Z параллелепипеда может быть опреде­лена как произведение температур для трех пластин:

0 = 0І0203. (2.209)

Для цилиндра конечной длины соответственно как произведение решений для бесконечного цилиндра и неограниченной пластины

0ц = 0102. (2.210)

Приведенные решения удовлетворяют дифференциальному урав­нению (2.208) и граничным условиям.

Теоремой о перемножении решений пользуются и при определении температуры в телах более сложных пересечений. Определение средних

6* 163
Температур для этих тел проводится по тем же правилам перемно­жения средних. Так, средняя температура куба определяется из соотно­шения

0fc = 6?. (2.211)

Регулярный тепловой режим. Анализ решений дифференциального уравнения теплопроводности показывает, что все они представляют собой быстросходящийся ряд. При Fo ^ 0,25 без особой погрешности можно воспользоваться первым членом ряда и представить решение, например, для неограниченной пластины в виде формулы

А = Лі cos (^i-jj e-tfFo, (2.212)

Или, опуская индексы и вводя обозначения, в виде

& = АРе~т (2.213)

Где А — постоянная, определяемая начальным распределением темпера­туры в теле; Р = cos (pix/5) — функция, зависящая от координат и Ві.

Нестационарный процесс теплопроводности, описываемый уравне­нием (2.213), называется регулярным тепловым режимом. Величина т = p2a/S2 называется темпом регулярного режима.

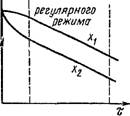
Логарифмируя уравнение (2.213), получим

In 0 = — тх + const. (2.214)

Из полученного уравнения следует, что логарифм относительной температуры есть линейная функция времени. Это положение сохра­няется для любой точки тела. На рис. 2.27 показано изменение температуры в точках хх и х2 при охлаждении тела. Автомодельность поля относительной температуры 0 во времени является характерной особенностью регулярного режима.

Дифференцируя уравнение (2.214) по времени, получим

1

Т = - - g-^r = ^ Ф - (2.215)

Из этого уравнения следует, что темп регулярного режима охлаж­дения (или нагревания) не зависит ни от координат, ни от времени, представляет собой относительную скорость изменения температуры, выражается в 1/с и в любой точке тела остается постоянным.

Темп регулярного режима определяется геометрической формой и размерами тела, его физическими свойствами и условиями тепло­обмена на поверхности тела.

Теория регулярного режима была разработана Г. М. Кондратьевым и применена им для определения теплофизических свойств тел и коэф­фициента теплоотдачи на поверхности тела, омываемого потоком жидкости. Например, при Ві оо величина т пропорциональна коэф­фициенту температуропроводности т= p.2 а/82, или

А = Km да. (2.216)

Коэффициент к в (2.216) называется коэффициентом формы, зависит

ІП19Ч

Стадия

Рис. 2.27. Автомодель - ность температурного по­ля при регулярном теп­ловом режиме

Лишь от геометрической формы и разме­ров тела и равен для параллелепипеда со сторонами 25ь 252, 283:

К

И 257

+

+

1

(2.217)

Тс

28;

(2.219)

257

Для цилиндра длиной I и радиусом г0 1

(2.218)

(2,405/го)2 4- (тс//)2 Для шара радиусом г0 1

К

(Фо)7

Режима легко определяются теплопровод - и коэффициенты а теплоотдачи. Методы отличаются простотой техники эксперимента и сравнительно небольшой затратой времени определения необходимых характеристик.

Численные методы. Метод конечных разностей. Аналитическое реше­ние задач теплопроводности может быть получено далеко не для всех случаев. Уравнение теплопроводности не всегда возможно решить аналитически для тел сложной геометрической формы или при сложных краевых условиях.

В связи с интенсивным развитием вычислительной техники в послед­нее время получил большое распространение конечно-разностный метод решения задач нестационарной теплопроводности, или метод сеток. Методом конечных разностей может быть решена практически любая задача теплопроводности с произвольными начальными и граничными условиями и переменными физическими параметрами тела.

Сущность метода конечных разностей состоит в замене дифферен­циального уравнения теплопроводности его конечно-разностным анало­гом. При этом тело рассматривают состоящим из конечного числа слоев и непрерывное распределение температуры в теле заменяется ступен­чатым.

Покажем на примере одномерной задачи нестационарной тепло­проводности особенности метода конечных разностей.

Методом регулярного ность (в ^.-калориметре)

Дифференциальное уравнение теплопроводности для неограничен­ной пластины:

D2T Дх2

Dt_ Дх

(2.220)

Заменим дифференциалы в уравнении (2.220) конечными прираще­ниями. Для этого разделим пластину на слои одинаковой толщины и обозначим их индексами п, п + 1,. По аналогии с разностной сет­кой для пространственных координат вводится сетка по временной переменной х. Индексы к, к + 1, ... характеризуют температуру в рас­четный момент времени Tk, ffc+1, Тогда T„Tk, например, означает

Температуру в слое п в момент времени к.

Аппроксимируя производную температуры разностными отноше­ниями, получим

Dt T{K + T), п ~ H,N .

(2.221)

Дх Ах

+ *) ~ " ■ Dt ^ Tki „ — Ffc; (и - 1)

Дх ~ Ах ' дх ~ Ах

Tk,(n + 1) ~ __ Frt, П ~ tfc, (л - І)

Д2г 1 <9х2 Ах

Ах Ах

Tk, <п+1) ~~ „ + Fft, (,|- 1)

Ах2

(2.222)

Заменяя производные в уравнении (2.220) их разностными выраже­ниями, получим

<,£+1)дх ~ = д^тГ^. (п+1) — Ltx „ -F- Tki („-Ij. (2.223)

Уравнение (2.223) является разностным аналогом дифференциаль­ного уравнения теплопроводности. Решим уравнение (2.223) относи­тельно f(fc +l),n-

А Ах / 2а Ах *<* + 1), П — дх2"1Л, (п - 1) + Tk, <„ + 1)J + } 1 J Tk,N- (2.224)

Уравнение (2.224) называется сеточным уравнением. Оно устанавли­вает связь между искомой температурой в точке п и температурами в предыдущий расчетному интервал времени к в соседних узлах сетки (п — 1) и (п + 1). При этом предполагается, что распределение темпе­ратур между точками (п — 1), п и (и + 1) является линейным. Чтобы решение было устойчивым, выбор значений Ах и Ах не может быть независимым, а должен подчиняться условию:

(а Ах)/Ах2 ^ 1/2. (2.225)

При несоблюдении этого условия решение становится неустойчивым, верный расчет не может быть получен, изменение температуры в процессе расчета принимает беспорядочный характер.

Значениями коэффициента [формула (2.225)] отличаются различные конечно-разностные методы. Наиболее простое решение соответствует условию (а Ах)/Ах2 = 1/2. В этом случае расчетное уравнение (2.224) принимает вид

, Tk, („_!, + Tkf (,,+ i) n ,,,, F(fc + U, n = у . (2.226)

В соответствии с формулой (2.226) температура определяется как среднее арифметическое температур соседних слоев (предыдущего и последующего) в предыдущий момент времени. Когда выполняется первый шаг по времени, значения температур берутся из начальных условий.

При граничных условиях третьего рода температуры поверхностей пластины для симметричной задачи Tk> 0 — fkj 5 и определяются из

Уравнения теплообмена:

(2.227)

И ~ h, о) == "70 ~~ l)(>

Откуда температура на поверхности пластины

(2.228)

В каждом расчетном интервале времени Дт уравнения (2.226) и (2.228) решаются столько раз, сколько интервалов (Дх) содержится в пространственной сетке. Разностная схема [уравнения (2.224) и 2.226)] называется явной, так как температуры Tk+I определяются по извест­ным значениям Tk в предыдущий расчетный момент времени. Точность расчета повышается при уменьшении Дт и Ах.

Кроме указанного метода для решения дифференциального урав­нения теплопроводности могут быть использованы другие явные и неявные конечно-разностные уравнения. Методы решения их приведены в специальной литературе. Решение системы конечно-разностных урав­нений выполняется, как правило, с помощью ЭВМ.