Неоднородными называются тела, макроструктура которых представляет конгломерат основного материала (связующего) и различных по свойствам, форме и размерам включений, чаще твердых или газообразных. К этой обширной группе относятся различного рода порошки и засыпки, пористые теплоиэоляторы и огнеупоры, ископаемые угли, коксы и целый ряд других при­родных и искусственных материалов.

В отличие от теплоемкости, которая не зависит от макро - структурных факторов, иа коэффициенты теплопереноса эти факторы оказывают большое, часто решающее влияние. С од­ной стороны, распространяющийся в неоднородном (пористом и трещиноватом) теле тепловой поток вынужден преодолевать сопротивление, обусловленное рассеянием (вещество связую­щего и границы зерен), удлинением пути и уменьшением живо­го сечения (поры) и, наконец, разрывами непрерывности (тре­щины). С другой стороны, влияние пор и трещин в некоторой степени компенсируется теплопроводностью заполняющего их газа и (при высоких температурах) радиационным теплообме­ном. Конвекция в порах дисперсного материала, как правило, пренебрежимо мала.

Влияние пористости

Для расчетов эквивалентной теплопроводности пористых ма­териалов предложено большое число формул, различающихся исходными моделями. Часть из них не учитывает влияние ра­диационного обмена в порах, и поэтому их можно применять при умеренных температурах либо в тех случаях, когда тепло­проводность связующего столь велика, что вклад радиационной составляющей пренебрежимо мал даже при высоких темпера-

3 Зак. 179 33
турах. Ниже приведены некоторые из наиболее употребитель-, ных формул.

Формула Максвелла, выведенная для модели «шары в ку-| бической кладке», имеет вид

1____ _____ « (2 + Хг/Хр) — 2р (1 К1Ю /тт 1 и«

А»экв Л0 (2+Хг/*о)+р(1-*г/*о) •

Где Я,0 — теплопроводность связующего; К — теплопроводность,, газа в порах; р— объемная концентрация газа (пористость),^ доли единицы.

При отсутствии теплопередачи в порах (Я, о!>Я, г) формула^ Максвелла преобразуется к виду

А. ЭКВ ~ А.0 ' j _|_ J^cjr • (II. 12)

Формула Максвелла дает удовлетворительное согласие с экс-;; периментом при малых значениях пористости.

Формула Русселя:

1 TOC o "1-5" h z 1 _______ р^3 ~ь (хрМг) (1 р2 о__________________ /тт 1 о vs

А° р2/3-р + (Х0/Ч(1-//з + />) • ( *

Формула Эйкена

1+2p.1 "zlojK

І » _____________ 1 + 2 Х0/Хг..

Я'экв_я'о_; і - Ло/Хг (ІІЛ4Ї!

1~Р 1+2^о. Дг

Дает результат, совпадающий с результатом, полученным по1 формуле (II. 12), если А<ДГ>1. ",

(1-Р„)+ Al

Формула Лоуба учитывает радиационный обмен в порах|

А. ЭКВ — A. Q

(11.151s

РарК +0-Рпр)

4^£1с1Т3

Где рп — пористость, отнесенная к поперечному сечению. Приг равномерном распределении пор рп=р2/3- рпР — пористость, от­несенная к продольному сечению; при равномерном распределен нии пор рпр=рг/3; — постоянная Стефана — Больцмана, рав| ная 5,7-10~8 Вт/(м2-К4); е — геометрический фактор; V — сте| пень черноты пор; д. — средний эффективный диаметр пор* Т—абсолютная температура поры. л

В отсутствие теплообмена в порах формула Лоуба приобрел тает очень простой вид:

А.»КВ«М1—р). (11-16)1

По некоторым данным [23], зависимость (II. 16) вполне - удовлетворительно описывает эквивалентную теплопроводность^ пористых углеграфитовых материалов с р^0,5 в интервале,’ 34

Температур 200—1700° С. Согласно другим данным [24], наи­лучшее приближение для графитов высокой пористости дает

Формула Русселя.

Формула В. И. Оделевского для системы с замкнутыми включениями кубической формы:

SHAPE \* MERGEFORMAT

(II 17)

1 - р

А. ЭКВ — ^0

1 — Хг/ Х0 3

При А, о»А, г формула (II. 17) дает результат, совпадающий с результатом, полученным по формуле (II. 12).

Все приведенные выше формулы выведны для статистиче­ски упорядоченных систем, обладающих трансляционной сим­метрией. В реальных случаях возможны поэтому значительные отклонения расчетных значений эквивалентной теплопроводно­сти от значений экспериментально найденных. Этим объясняет­ся широкое распространение полуэмпирических зависимостей для расчета теплопроводности пористых структур.

Так, А. Миснар, рассматривая альтернативные структуры [25] (систему сплошной твердой фазы с газообразными вклю­чениями и газовую фазу с твердыми включениями), считает, что теплопроводность всех реальных пористых тел может быть представлена как линейная комбинация соответствующих ко­эффициентов теплопроводности А/ и К":

(11.18)

А'ЭКВ — 0.%' ,

Где (в принятых обозначениях)

1 +р- 1 +В

(11.19) (11.20)

1 - *оДг

1 — р'/з (1 - Ао/М

1 - Лг/Х

1 - В‘/э(1 - ХГД0)

-6 = 1—р, а и Ь — эмпирические коэффициенты. По данным А. Миснара, для каменных углей и коксов коэффициенты а и Ь равны соответственно 0,4 и 0,6.

Пренебрегая теплообменом в порах, формулы А. Мисна­ра можно упростить:

>/=Хо(1 ~РЪ). (П.21)

Теория теплопроводности систем с взаимно проникающими компонентами, представляющая практический интерес приме­нительно к телам с большой долей открытых пор, построена Г. Н. Дульневым [26, 27].

Влияние трещин

Трещины оказывают на теплопроводность твердого материа­ла наибольшее влияние в том случае, если тепловой поток рас­пространяется перпендикулярно к их преимущественной ориен-

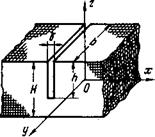
Рнс. 3. Модель твердого тела с поперечной трещиной

Тации. В другом предельном случае (направление теплового потока совпадает с ориентацией трещин) их влияние сводится " лишь к некоторому, как правило, незначительному уменьшению живого сечения материала. Поэтому здесь будет рассмотрен только первый случай.

На рис. 3 изображена модель твердого тела с поперечной трещиной средней шириной б, которая заполнена газом тепло-, проводностью А*. В направлении оси х распространяется стаци-' онарный тепловой поток С. На поверхностях 2=0, г—Н, у=0к, у=Ь поддерживаются адиабатические условия. Пренебрегая’* искривлением температурного поля, вызванным трещиной, т. полагая, что во всех сечениях

ДТ дТ -

Ду ~ дг и’

Найдем тепловые потоки через трещину 0,' и через твердый ма% териал 0.".

Т, - г,

Тепловой поток через трещину должен включать кондуктив ную и радиационную составляющие:

<2' =<3/Р+<2/к = ^'( 7У - ЗГ,4) +№'

Где ^ — постоянная Стефана — Больцмана (см. выше); степень черноты поверхности трещины; Р'—поверхность щины; Т1 и Т2—абсолютные температуры поверхностей щины (Т2>Т 1).

Полагая перепад температуры на границах трещины большим, заменим выражение для С}'р приближенным:

Тогда

Тепловой поток через твердый материал Q" = F"%" ~ ,

Где %" — эквивалентная теплопроводность твердого материала, в общем случае пористого.

Эквивалентная теплопроводность рассматриваемой модели

Лэкв = а (<^67*+А*) + (1 -а) X", (11.22)

__ F' h

Гд еи-у (в данном случае а = I-

При произвольной ориентации трещины относительно тепло­вого потока.

Лэкв = (tyv8T3Jrlг) a cos | ф11 cos | <р21 +

+Л"(1— acos |ф!| cos |q>21), (11.23)

Где ф! И ф2 — углы между нормалью к поверхности трещины и

Ее проекциями на плоскости хоу и xoz соответственно

(см. рис. 3). Как и прежде, a—F'/F.

Легко заметить, что' если один из углов <р равен я/2, т. е. трещина ориентирована вдоль потока, то эквивалентная тепло­проводность равна теплопроводности твердого материала (ко­нечно, с учетом его пористости).

При наличии в образце нескольких трещин его эквивалент­ная теплопроводность может быть рассчитана по формуле

<п-24>

Теплопроводность засыпок дисперсных материалов

При изучении теплофизических свойств неоднородных мате­риалов для получения сопоставимых результатов часто прибе­гают к дроблению образцов. Значения коэффициентов теплопе - реноса, полученные в таких экспериментах, значительно мень­ше по абсолютной величине. Они имеют, как правило, иные температурные зависимости, нежели в случае монолитных об­разцов, и характеризуются в то же время хорошей воспроизво­димостью, если выдерживаются необходимые для этого усло­вия, что позволяет в ряде случаев сопоставлять их с теплофи­зическими характеристиками исходных образцов.

Эквивалентная теплопроводность дисперсного материала яв­ляется сложной функцией его плотности и гранулометрического состава, теплопроводности твердой и газообразной фаз, темпе­ратуры, плотности упаковки и ряда других факторов. Попытки

37

Учесть взаимное и результирующее влияние этих факторов при­водят к весьма сложным зависимостям, применение которых на практике затруднительно.

Анализ этих зависимостей и экспериментальных данных, от­носящихся к рассматриваемому вопросу, позволяет сделать сле­дующие выводы.

Эквивалентная теплопроводность засыпок в гораздо мень­шей степени зависит от теплопроводности твердой фазы, чем в случае пористых тел.

Роль теплопроводности газа в порах и радиационного теп­лообмена соответственно значительно выше.

Теплопроводность засыпок, как правило, повышается при укрупнении частиц. Влияние диаметра частиц на эквивалент­ную теплопроводность увеличивается с ростом температуры. При комнатных температурах теплопроводность мало изменя­ется с ростом диаметра частиц.

Теплопроводность засыпок можно рассчитывать по формуле (11.18), измерив значения эмпирических коэффициентов а и Ь. По нашим данным [28], для измельченного (<0,25 мм) ка­менноугольного кокса эти коэффициенты равны соответственно

0, 2 и 0,8.

Измерения теплопроводности измельченных углей, выпол­ненные М. Вике и В. Петерсом [29], позволили им предложить следующие эмпирические формулы для расчета А, ЭкВ:

Антрацит

^экв = 0,083(д.)°’063-1-20,6• 10~~5(й)°’1317', ккал/(м-ч-°С), (11.25).

Где й — средние диаметры зерен, мм; Т — температура, °С. По­грешность расчета по формулам (II. 25) и (II. 26) в интервале температур 50—200° С и диаметров частиц от 0,4 до 4 мм не превышает, по данным [29], 2%.

Там же показано, что для тепло - и температуропроводности смесей нескольких фракций хорошо выполняются аддитивные соотношения:

(11.27)

Пт — £СІ-- £2<І2,

(11.28)

Кт — ё 1 ~~ А,1+§2 *

Рі Р2

Где индексы «1» и «2», «т» обозначают первую и вторую фрак­ции и их смесь; g — массовая доля фракции в смеси; р — ка­жущаяся плотность.