V/ Закон Планка

Тепловое и световое излучения представляют собой, как из­вестно, электромагнитные колебания, различающиеся лишь длиной волны и распространяющиеся в вакууме со скоростью 300000 км/сек. Следовательно, распространение света и тепло­вого излучения в противоположность звуковым волнам и ощу­щаемому теплу не связано с материей *. Нагреваемое твердое тело испускает лучи, характеризуемые волнами от самых ма­лых до самых больших длин, причем интенсивность излучения по различным длинам волн очень различна. Знание зависимости интенсивности излучения от длины волны и температуры имеет большое теоретическое и практическое значение, так как оно дает возможность конкретно определить свойства данного из­лучения. Эта важная зависимость для излучения абсолютно черного тела выражена М. бланком в законе излучения. Абсо­лютно черное тело — это такое тело, которое поглощает, не от­ражая, все падающие на него лучи независимо от длины их волн. Основываясь на излагаемом ниже законе излучения Кирх­гофа, такое тело дает максимальное излучение, которое воз­можно при этой температуре как тепловое. Излучение абсолют­но черной поверхности называется черным излучением, даже если в нем содержится любое количество световых лучей. За-

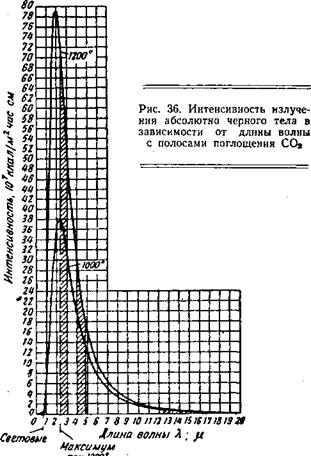
Кон Планка для черного излучения двух тел с температурами 1000 и 1200°С представлен на рис. 36. Ординаты этих кривых показывают интенсивность излучения волны соответствующей

Длины. Видно, что при 1200°С практическое значение имеют лишь волны длиной от 1 до 15ц (1ц = 1000 мм). Эти волны от­носятся к инфракрасному невидимому тепловому излучению. Видимое световое излучение занимает лишь область длин волн от 0,4 до 0,8 ц и, как показано на рис. 36, при 1200° С не влия­ет на тепловое воздействие общего излучения. Из этого следу­ет, что световые лучи при используемых в технике температу­рах играют лишь подчиненную роль и наибольшая часть тепла передается посредством невидимого теплового излучения. При 16*

Более высоких температурах доля световых лучей в общем из­лучении становится все больше,, так как максимум кривой с по­вышением температуры смещается в область более коротких длин волн (закон смещения Вина) и, наконец, при температуре солнца 6000°С световые лучи дают приблизительно половину излучаемой энергии. Необходимо учесть, что при поглощении света поверхностью выделяется точно такое же количество теп­ла, как и при поглощении невидимого теплового излучения. Это понятно, так как световое излучение отличается от невидимого теплового лишь тем, что случайно действует на глазной нерв человека, который «настроен» на соответствующую длину вол­ны. Следовательно, глаз не видит важное для технической теп­лопередачи излучение, между тем как его познание важно для оценки излучения так называемых несветящихся пламен. За­кон излучения Планка, как явствует из рис. 36, для двух тем­ператур описывается следующей формулой:

Л =3,17 • 10~8 •------------------ ккал/ма- час • см[149], (391)

1,43 6^-1

Где Л — интенсивность лучей С ДЛИНОЙ ВОЛНЫ, (Д.;

X —длина волны, см

Т — абсолютная температура облучаемой черной по­верхности, °К[150]. (Т = Р С + 273).

Распределение длин волн >по уравнению (391) для температур, равных 1000 и 1200°С, изображено на рис. 36.

Закон смещения Вина

Если формулу Планка продифференцировать по Я и по известному методу определить длину волны, которая соответ­ствует максимальной интенсивности, получим закон смеще­ния Вина:

Ьмакс - Т = 2880 [X °к. (392)

Этот закон был. выведен иным путем В. Вином еще раньше Планка.

Из уравнения (392) следует, например, что максимум излу­чения солнца с температурой фотосферы 6000°К находится при
% = 0,48 |а, следовательно, в коротковолновой части видимого излучения.

Большая часть энергии солнечного излучения, как уже ука­зывалось выше и как Следует из формы кривой Планка, лежит в области видимого излучения, что не является правилом для земных излучателей. Следовательно, тепловое воздействие сол­нечного излучения в подавляющем большинстве случаев основа­но на поглощении света облучаемым телом. Напротив, макси­мум излучения, например, комнатной печи с температурой по-

2880

Верхности 100°С лежит в области --------------- = следова-

373

Тельно, в инфракрасной области длинных волн и далеко от обла­сти любого светового излучения.

Закон Стефана — Больцмана

Если величина (II длинноволновой области излучения оп­ределяет интенсивность Л, то ее тепловое воздействие в едини­цу времени (энергия) равно произведению Л'^х. Сумма энергии J^kd} всех длин волн, излучаемых телом, дает его общее излучение. Поэтому оно представляется площадью, об­разуемой кривой Планка и осью абсцисс (см. рис. 36). Как вид­но из обеих кривых, общее излучение очень быстро возрастает с повышением температуры, а именно (как установил на опыте Стефан еще раньше Планка): увеличивается пропорционально четвертой степени абсолютной температуры черного тела. Позд­нее Больцман теоретически обосновал этот закон для черных тел. Закон Стефана — Больцмана является основным для расчета излучения твердых и жидких тел, встречающихся в технике.

Он гласит

В этом уравнении:

С — коэффициент излучения, ккал/м2 - час • град4-,

.Г — излучающая или облучаемая поверхность, м

Тх — абсолютная температура излучающей поверхности, °К; Т2 — абсолютная температура облучаемой поверхности, °К. Закон излучения Стефана — Больцмана, строго говоря, совер­шенно справедлив лишь для абсолютно черных поверхностей. Такие поверхности излучают максимально возможное количест­во тепла и их коэффициент излучения максимален при данных

Условиях [151]. Новейшие измерения коэффициента Со абсолютно черного тела дают значение в

С0 = 4,96. (394)

Излучение поверхностей, встречающихся в действительности, по своим свойствам всегда более или менее отклоняется от из­лучения абсолютно черного тела. Этот вопрос будет разобран ниже.

Уравнение (393) справедливо как для отдачи, так и для вос­приятия (поглощения) лучей, т. е. безразлично, будет ли темпе­ратура Т% меньше или больше температуры Т. Если Т2>Т 1, то уравнение (393) отражает случай поглощения изл^ае^юй энергии поверхностью Р с температурой Ти

Относительно выбора поверхности Т7 справедливо следующее: если две поверхности находятся в условиях теплообмена излу­чением, причем одна поверхность полностью окружает другую, то в качестве поверхности Р в уравнении (393) /всегда подстав­ляют меньшую, т. е. охватываемую, поверхность независимо от’ того, идет ли речь о поглощении лучей или о лучеиспускании. Так, например, при расчете тепла, воспринимаемого жаровой трубой за счет излучения от лежащего в ней колосника, в фор­мулу вместо Г подставляют значение поверхности колосника, а нежаровой трубы.

Если поверхности, обменивающиеся излучением, не охватыва­ют одна другую, а расположены под любым углом друг к другу так, что только какая-то доля общего излучения будет попадать на облучаемую поверхность, а остальная часть проходит мимо нее, то справедливы нижеследующие рассуждения (стр. 400—401).

Если же рассматриваемая часть поверхности расположена так близко к другой поверхности, что все идущее от нее излучение должно достигать другой поверхности (она как бы «не видит» ничего, кроме другой поверхности), то этот случай будет аналогичен описанному выше^ (когда одна поверхность охва* тывает другую) и все сказанное справедливо для него. Поэтому под поверхностью понимают величину рассматриваемой части поверхности, и общее излучение или поглощение определяют по уравнению (393) [152].

Закон излучения Кирхгофа

Между излучательной способностью тела (она пропорцио­нальна коэффициенту излучения С) и поглощательной (пропор­циональной степени черноты 5) существует зависимость, кото­рая определяется законом Кирхгофа: коэффициент излучения лю­бого тела при определенной температуре и определенной длине волны пропорционален поглощательной способности рассматри­ваемого тела при той же самой температуре и длине волны. Сообразно с этим тело при данной температуре излучает тем больше тепла, чем сильнее оно поглощает лучи, т. е. чем ближе оно к абсолютно черному телу. Поэтому, согласно закону Кирх­гофа, абсолютно черное тело, которое поглощает все падающие на него лучи, излучает максимально возможнее количество тепла. Оно имеет поглощательную способность, или степень черноты, -

5 = 1. Следовательно, степень черноты всех не абсолютно черных тел будет меньше единицы. Математически закон Кирхгофа можно выразй'ть соотношением

С — А • 5 ккал/м2 • час • град*, ' (395)

Где к — коэффициент пропорциональности. Так как для абсо­лютно черных тел 5=1 и С — 4,96, то из уравнения (395) & =

(395а)

= 4,96 и уравнение (395) преобразуется в

С = 4,96 • 5.

Полированное серебро, которое поглощает всего лишь несколько процентов падающего излучения, характеризуется, следователь­но, очень маленьким коэффициентом излучения С. Закон излуче­ния Кирхгофа может быть доказан рассмотрением температурно­го равновесия в закрытом объеме на основе положений термоди­намики. Следовательно, закон абсолютно справедлив лишь для тех случаев, когда речь идет о чисто тепловом излучении, а не

Об излучении, которое можно объяснить другими причинами (лю­минесценцией, фосфоресценцией и т. д.). В табл. 45—52 прило­жения даны известные на сегодня коэффициенты излучения С чаиболее часто применяемых веществ.

Закон излучения Ламберта

(396)

Этот закон указывает, что излучение поверхности в направ­лении, не перпендикулярном к ней, изменяется пропорциональ­но косинусу угла между лучом и нормалью к поверхности. Сле­довательно, если угол, который образует луч с нормалью к по­верхности, равен ф°, то количество энергии, излучаемой в этом направлении,

<2 = • соэ <р ккал/час.

Здесь Цп — количество тепла, излучаемое перпендикулярно к поверхности. Однако этот закон излучения Ламберта для многих тел справедлив лишь приближенно. Но он справедлив всегда, если данное тело излучает диффузионно, т. е. не зеркально отра­жает падающие лучи, а рассеивает их во все стороны, как например матовая белая поверхность мела. Диффузионное рас­сеяние света вызывается очень мелкими неровностями поверх­ности, которые представляют собой маленькие зеркала, нерав­номерно расположенные по всем направлениям. Закон Ламберта не справедлив для металлов с блестящей поверхностью; в этом случае, наоборот, излучение в направлении, не перпендику­лярном к поверхности, буд^т интенсивнее, чем в перпен­дикулярном [153].

Из закона Ламберта путем интегрирования определяем излу­чение в направлении, нормальном к поверхности,

(397)

Qn = fofo- ккал/час,

Где <2общ — общее излучение излучающей поверхности, опреде­ляемое по закону Стефана—Больцмана [уравнение (392)]. Сле­довательно, уравнение (397) примет следующий вид:

(398)

Из этого уравнения определяют величину (}п и подставляют ее в уравнение (396).

Зависимость интенсивности излучения от расстояния. Интен­сивность излучения («яркость» излучения) точечного источника уменьшается пропорционально квадрату расстояния от источни­ка излучения. Следовательно, интенсивность излучения

(399)

Где /1 — интенсивность излучения на расстоянии 1 м от источ­ника излучения и г — расстояние от источника излучения, м. Этот закон справедлив для всех случаев, так как поверхность
сферически распространяющихся волн при увеличении радиуса: растет пропорционально квадрату этого радиуса; следовательно, излучение должно распределяться по поверхности, увеличиваю­щейся пропорционально квадрату расстояния от источника излу­чения (точечного). Напротив, закон справедлив тем меньше, чем~ больше размеры источника излучения по отношению к расстоя­нию г. Эту зависимость можно хорошо проследить математиче­ски. Так, расчет показывает, что интенсивность излучения бес­конечно большой стенки с увеличением расстояния от нее не уменьшается, а остается постоянной. Это имеет большое значе­ние при измерении интенсивности излучения: показания пиромет­ра не зависят от расстояния до визируемой поверхности излуче­ния, так как эта поверхность заполняет все поле видимости пи­рометра, для которого, следовательно, она должна рассматри­ваться как бесконечно большая. Интенсивность излучения телг которые нельзя считать ни точечными, ни бесконечно большими, уменьшается пропорционально расстоянию г в степени от 0 до 2. Значение показателя степени зависит от соотношения размеров тела и расстояния г.