Смешение — это механический (а иногда и механохимичсский процесс), целью которого является превращение исходной систе­мы, характеризующейся упорядоченным распределением компо­нентов смеси, в систему, характеризующуюся неупорядоченным, статистически случайным распределением.

В результате процесса смешения в смесителе происходит вза­имное перемещение частиц разных компонентов, расположен­ных до перемешивания отдельно или находящихся в неоднород­но внедренном состоянии. Смешение широко применяют в са­мых разнообразных отраслях промышленности, в том числе в технологии производства и переработки полимерных материа­лов, так как чистый полимер в подавляющем большинстве случа­ев не обладает нужным комплексом свойств и не может быть ис­пользован для изготовления изделий. При переработке полимер­ных материалов смешение используют для введения в перерабатываемый полимер пластификаторов, наполнителей, красителей, стабилизаторов и других добавок. Процесс смеше­ния можно осуществлять в системах «твердое вещество — твер­дое вещество», «жидкость — жидкость», «твердое вещество — жидкость*.

Различают два основных вида процессов смешения: периоди­ческий и непрерывный.

Периодический процесс смешения применяется в подготови­тельных производствах (7J. Он характеризуется тем. что все пере­мешиваемые компоненты одновременно (или в определенной последовательности) вводятся в некоторый замкнутый объем, и процесс смешения продолжается до тех пор, пока не будет достиг­нута необходимая степень однородности распределения компо­нентов.

Непрерывный процесс смешения — это процесс, в котором за­данная степень однородности распределения достигается за время одного прохода смешиваемого материала через рабочую полость смесителя. В этом случае обычно все компоненты загружаются в одном месте (на входе), а ютовая смесь выгружается в другом (на выходе). Загрузка и выгрузка осуществляются непрерывно. Ти­пичным представителем смесителей непрерывного действия явля­ются экструдеры. Однако при экструзии возможны два варианта загрузки исходных компонентов: 1) загрузка в экструдер предва­рительно смешанных компонентов; 2) загрузка компонентов через несколько бункеров или в один бункер с помощью дозатора весо­вого или объемного типов 110).

Ирм анализе процессов смешения в одношнековых жструдерах предполагают,

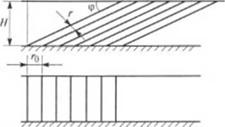
Рис. 2.51. Уменьшение то. пцины полос от г* до г при деформации сдвига у = L/II

•мо смешение начинается в юне плавления полимера и свершается в зоне дозиро­вания.

Следовательно, предпо - 1агается, что в зоне загруз­ки практически отсутствует смешение полимера с дру­гими компонентами. При ном расплав полимера рас­сматривается как высоко - вя жая жидкость, а смеше­ние называется ламинарным, так как в этом случае число Рей­нольдса Кс«1. Впервые анализом процесса ламинарного смешения занимались авторы работы |47|. Дальнейшее разви - гие теория ламинарного смешения получила в работах |4, 46. 48|. Во всех указанных работах качество смеси при ламинарном смешении предлагается оценивать толщиной полосы, право­мочность применения которой для этого доказана в работах 149—51]. Толщину полосы находят как среднее расстояние между двумя слоями одного и того же компонента в системе (рис. 2.51).

Рис. 2.51 иллюстрирует уменьшение первоначальной толщины полосы г0 в жидкой системе (одна жидкость окрашена в черный цвет, другая — в белый), расположенной между двумя параллель­ными плоскостями. При этом жидкость смачивает стенки, причем нижняя плоскость неподвижна, а верхняя движется относительно нижней со скоростью К Плоскости удалены друг от друга на рас­стояние //. При движении в жидкости возникает деформация сдвига Г= /./// = ctg Ф. При этом происходит уменьшение тол­щины полосы от начального значения /ьло конечного значения г (см. рис. 2.51).

Мор с соавторами |47| впервые получил уравнение, связываю­щее г0 с г в виде:

ЯГ Рс

(2.234)

те у — деформация сдвига, которая рассчитывается как Г у/; у — скорость сдвига, равная у dv/dу, I — время; q — доля наименьшего но концентрации компонента смеси; - вязкость наименьшего но концентрации компонента (и наполненных полимерах — это вязкость чистого полимера); цс — вязкость сис - ц*мы (наполненного полимера)

Мри добавлении красителя или небольшого количества напол­ни юля можно принять, что Цк = Щ;.

г

(2.235)

г = —-, или г =

П) яГ

я?

Автор работы |4| показал, что при ламинарном смешении боль­шое нлиинис на процесс оказывает поверхность раздела компо­нентов в системе. Чем больше поверхность раздела, тем лучшее качество смеси достигается.

Увеличение площади поверхности раздела зависит от перво­начальной ориентации поверхности и величины деформации сдвига. Максимальное увеличение площади поверхности разде­ла, т. е. наилучшее смешение, достигается тогда, когда поверх­ность раздела перпендикулярна направлению сдвиговой дефор­мации.

При этом следует отметить, что реальный материал ха­рактеризуется целым спектром толщины полос г как из-за раз­личия Гд в исходной системе, так и вследствие неоднородности ноля деформации сдвига /' в реальных смесителях (экструде­рах).

Авторы работ (7, 46J, рассматривая уменьшение толщины по­лос гири двухосной деформации сдвига, получили уравнение

(2.236)

'О " «[IWd]

с учетом, что в зоне дозирования одноишекового эксгрудсра Гх» 1, /'.» 1.

Аналогично для трехосной деформации сдвига:

_ г

В этих же работах при анализе многоосной деформации сдвига с учетом поверхности раздела и объема смеси получено выраже­ние:

(2.237)

Толщина полосы зависит не только от величины деформации сдвига, но и от характерного размера г0 частиц и доли добавляе­мого компонента. Применение относительной толщины полосы '7 = r/(/b|/•=(>) позволяет исключить из приведенных выражений исходные характеристики смеси [7, 46| при одноосной, двухосной и трехосной ле(1юрмации сдвига:

(2.238)

3

гх+гy + rz

При этом предлагается |52, 53| системы с различной средней пел ими ной г разбить на классы и оценку производить путем визу­ального, качественного сравнения с образцами. Эта оценка не ли­шена субъективности, однако создаваемые сейчас приборы, вы­полняющие автоматическое измерение набора г, в образце и ус­реднение г с учетом доли каждой rh устраняют этот недостаток.

Теоретический подход основан на вычислении величины /'час - 11ШЫ по соотношению J38|

/

о

и d/ = - dj, v

и in, при учете

чгсь г — время; воля линейных скоростей и скоростей

• пина массы деформируемого материала, в которой перемешается частиua; п, s — I* к i гоиним и направлении нормали к вектору скорости v ив направлении траск - |.||ши частицы.

И работе (55| получена формула для расчета Г на выходе из ка­нала;

> к /. Л — длина и глубина канала соответственно, а = у/h — координата глубины ».мыла; ф — ко:>ффиииснт дросселирования (см. раздел 2.7.1).

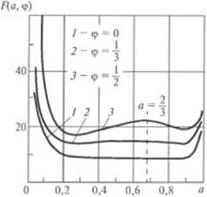
Нид ha, ф) приведен на рис. 2.52. Примечательно, что практи­чески на 70 % полного интервала изменения она имеет плато значе­нии, близких к минимуму. Если же учесть, что область 0 < а < 0,2

(область у стенки винтового ка­нала шнека) вносит очень ма­лый вклад в расход из канала, то согласно И(а, ф) степень сме­шения на выходе из канала до­вольно однородна. Этот факт позволил автору работы |48| предложить упрошенный под­ход, заключающийся в том. что степень смешения всего мате­риала можно оценить по ве­личине Г2/з = Г(а, ф)|о,/3: при этой координате функция ta, ф) имеет очень простое аналитическое выражение:

Рис. 2.52. Функция распределения на­копленной материалом деформации един га Г в поперечном сечении шнека (на вы­ходе И) него)

(2.239)

1,67 + ф 1-Ф

так что

(2.240)

/I 1-ф

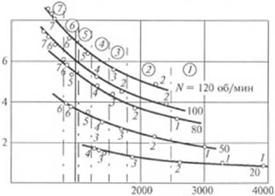
Экспериментальные данные 1521 подтверждают применимость формулы (2.240) для приближенной оценки качества смешения экструдата. Так, из графика на рис. 2.53 видно, что при самых различных режимах экструзии существует хорошая корреляция

Q, об/мим 1000 Деформация сдвига. Г2/} Рис. 2.53. Зависимость накопленной деформации с. шига Г от режимов дкетрулии. Цифры на кривых — пока и ими качества смеси: / — наилучшсс качество: 7— наихудшее качество

между величиной Г и экспериментальной визуальной оценкой качества смешения по классам. Длина L участка канала шнека, полностью заполненного расплавом, измерялась в опытах при из­влечении шнека из цилиндра после каждого опыта.

Давая общую оценку результатов работы |46—48, 54|, можно отметить следующее:

1) допущения о ньютоновском поведении расплава при сдви­говом деформировании и об изотермичности этого процесса в канале шнека приводят к искажению (в сравнении с реальными) скоростных профилей, однако это искажение, по-видимому, не может вызвать существенных ошибок в определении развиваю­щейся в дозирующей зоне суммарной деформации (и, следова - гсльно, степени смешения), оцениваемой по формуле (2.235);

2) приведенный метол оценки степени смешения (2.240) при­меним для дозирующей зоны, и, по-видимому, вследствие подоб­ной же кинематики движения расплава, только для жидкого ядра переходной зоны.