Ввиду сложности статистического метода применительно к развито­му свободному турбулентному течению были разработаны полуэмпири-

92

Ческие теории. В частности, Л. Прандтлем разработана теория переноса' количества движения, а Г. Тейлором — теория переноса завихренности.

Физическая модель механизма турбулентного движения была пред­ложена Л. Прандтлем в 1925 г. в следующем виде. В турбулентном те­чении возникают жидкие комки, т. е. элементарные конечные объемы жидкости, или, как их называют, моли, каждый из которых на протя­жении некоторого расстояния, называемого длиной пути смешения, дви­жется в виде единого целого с собственной скоростью, сохраняя коли­чество движения, а пройдя это расстояние, смешивается с окружающей жидкостью.

В установившемся осредненном потоке, направленном вдоль оси х со скоростным профилем и=0(у), выделим площадку направлен­ную вдоль течения (рис. 6-1). Вследствие наличия поперечных пульса - ционных скоростей за промежуток времени йх из слоя у со скоростью О (у) через площадку с1Э протекает в слой у + 1т со средней скоростью - О{у + и) масса жидкости рУ'йЭйх, количество движения которой при

Этом изменится на величину рУ'йЭйт/т

Согласно теореме импульсов изменение количества движения рав­но и противоположно по знаку импульсу сил, с которой окружающая среда действует на площадку за тот же промежуток времени, т. е.

РУ%^й8йх= — Рйг.

(6-27)

Относя уравнение (6-27) к единице площади и времени и учитывая,

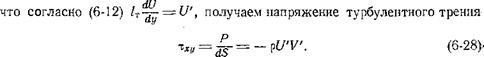
При распределении скоростей, соответствующем рис. 6-1, частицы жидкости, поступающие в рассматриваемый слой снизу, имеют положи­тельную поперечную пульсационную скорость и создают в ней отрица­тельную продольную пульсацию. Напротив, частицы, поступающие •сверху, имеют отрицательную поперечную пульсацию и создают положи­тельную продольную пульсацию. Поэтому произведение и'У'<0. Из-за наличия пульсаций возникает сила со стороны верхней части потока в положительном направлении оси х, дающая дополнительное напряже­ние трения х. В результате верхняя часть ускоряет нижнюю, а нижняя часть создает сопротивление для верхней.

Приняв, что поперечные и продольные компоненты пульсационной скорости одного порядка, подставив их значения согласно (6-12) в (6-28) с учетом того, что их произведение имеет отрицательный знак,, получим формулу турбулентного трения:

(6-29)

ЪХу = =£; р/!

, dlJ_ <Ш_ т йу йу ’

Уравнение (6-29) записывается в таком виде для того, чтобы пока­зать, что знак хХу должен быть таким же, как и знак производной (Ш/с1у.

Формула (6-29) показывает, что турбулентные касательные напря­жения пропорциональны квадрату скорости, и содержит одну неизвест­ную величину — длину пути смешения, являющуюся функцией у. По теории Прандтля в случае движения жидкости в трубах длина пути сме-

Шения возрастает с удалением от стенки пропорционально расстоянию от нее до рассматриваемой точки, т. е.

(6-30)

/т = ш/,

Где а — некоторая постоянная величина.

Таким образом, напряжение турбулентного трения определяется по­перечным переносом продольной составляющей количества движения.

Из (6-29) следует, что по известному полю скорости и значениям Тху можно вычислить величину пути смешения. И. Никурадзе на основе измерений распределения скоростей в круглой трубе получил, что /т на разных расстояниях от стенки изменяется в пределах от 0 до 0,14 ра­диуса трубы.

(6-31)

Т. Карман, стремясь освободиться в выражении для т от длины пути смешения, пришел к выводу, что ее можно выразить через извест­ные гидродинамические величины, а именно

Йу2

Причем коэффициент х иолучился постоянным и равным

И=0,38-*-0,40.

По аналогии с законом для касательного напряжения в ламинар­ном течении Т. В. Буссинеск предложил для определения турбулентного касательного напряжения следующую формулу:

(6-32)

Величина А по аналогии с коэффициентом вязкости в законе тре­ния для вязкой жидкости Ньютона рассматривается как коэффициент некоторой воображаемой «турбулентной» вязкости. Соответственно ве - . личина А/р = ет, рассматриваемая как коэффициент кажущейся кинема­тической вязкости турбулентного течения, называется коэффициентом турбулентного обмена. Коэффициент турбулентной вязкости во много и даже сотни раз превышает коэффициент вязкости ламинарного тече­ния. Только в непосредственной близости к стенке величина А сравнима с величиной р, причем на самой стенке А= 0. В связи с этим в потоке, кроме области, непосредственно примыкающей к стенке, и в свободных потоках можно пренебрегать вязкими напряжениями по сравнению с турбулентными.

Формула (6-32) обладает тем недостатком, что коэффициенты А и 8Т не являются физическими константами жидкости, а зависят от ско­рости и. Поэтому для возможности использования формулы (6-32) не­обходимо эмпирически найти связь между коэффициентом А и полем осредненны»х скоростей.

Сравнивая выражение (6-29) и (6-32), видим, что коэффициент турбулентной вязкости

(Ю_

А = р/2т СІу

А кинематической вязкости турбулентного течения ет, м2/с, выражается формулой

(1у

(6-34)

Вычислим теперь изменение х — составляющей количества движе­ния. За промежуток времени сіх сквозь площадку йБ, перпендикуляр­ную оси х, протекает масса жидкости рс?5Шт и переносит с собой ко­личество движения, равное рсіЗиМх. Осредняя скорость во времени» получаем изменение количества движения за единицу времени

(6-35)

Так как

То

Ии' = ии' = О,

Р^2 = Р ^(17*+ £7^).

Вследствие переноса количества движения возникает сила, с кото­рой окружающая среда действует на рассматриваемую площадку, чис­ленно равная и противоположная по знаку изменению количества дви­жения. Последнее означает, что на площадку перпендикулярно оси х действует сила, направленная внутрь поверхности, как давление с на­пряжением —р {й2+и^).

Слагающая

О = — риг 2 (6-36)»

Является дополнительным нормальным напряжением, вызванным нали­чием пульсационных скоростей.

Представляя физическую модель турбулентности как перенос вих­рей, Т. Тейлором получено, что

'Д/у

2 г" т йу) '

Эта формула отличается от формулы Прандтля (6-29) только мно­жителем 1/2. Последнее означает, что длина пути смешения в теории, переноса завихренности в У 2 раз больше длины пути смешения в тео­рии переноса количества движения.