Подвижные источники теплоты можно представить в виде по­следовательности элементарных мгновенных источников, смещен­ных в пространстве и во времени.

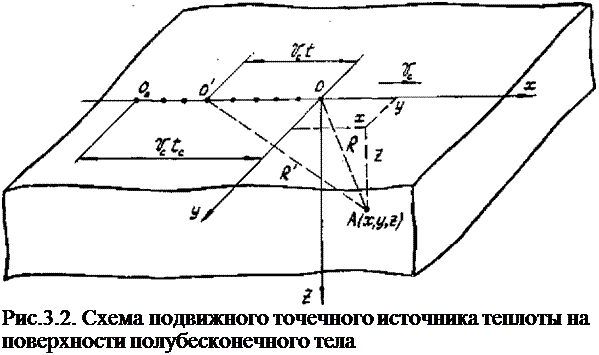
I. Пусть точечный источник теплоты постоянной мощно­

сти ^ движется с постоянной скоростью vt ИЗ ТОЧКИ 0О вдоль оси х и через время tt находится в точке О (рис.3.2). Найдем температуру в точке А в подвижной систе­ме координат х, у,а. , начало которой совпадает с точечным источником 0 . Мгновенный точечный источник, которых; дейст­вовал в точке 0' в течение времени dt, выделил теплоту

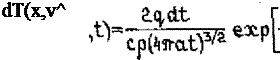Q = ^cLt. Через время t согласно уравнению (3.7) этот источник повысил температуру в точке А, расстояние до ко­торой "R1 =|/(x+v£t')a + уа + а1 , на величину

Суммируя приращения температуры от всех элементарных источников за все время tt, получим

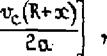В подвижной системе координат температура точки воз­растает, но через некоторое время (t—-=-» ) она достигает предельного значения, т. е. температурное поле относительно источника становится как бы неподвижным. Поэтому такое поле называется квазистгщионарным. В этом случае уравнение (3.II) интегрируется и несобственный интеграл принимает вид

■R-/xa + ^+K.£ ; ^ - мощность источника теплоты,

с. Аналогично с помощью уравнения (3.8) можно получить

уравнение квазистацпонарного температурного поля для случая подвижного линейного источника теплоты в бесконечной пласти­не

т^х>1йеЧ_^М^) ’ (злз)

где г=/хг+уг ; К0 - функция Бесселя второго рода нулевого порядка от мнимного аргумента; - коэффициент, учи­тывающий влияние "поверхностной теплоотдачи.

3. Для случая нагрева бесконечного стержня подвижным - источником теплоты квазистационарное температурное поле опи­сывается уравнением

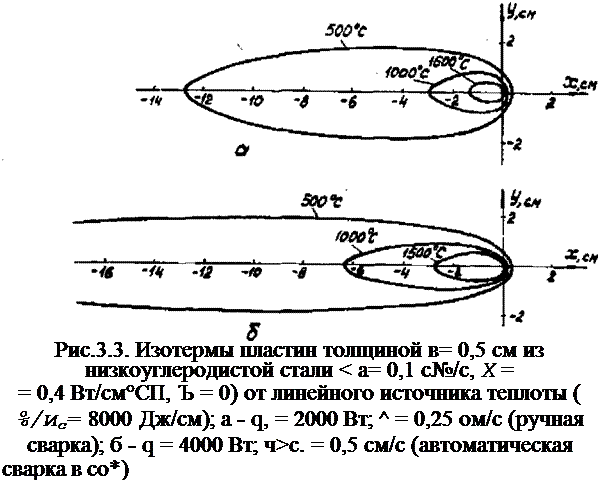
В качестве примера на рис.3.3 показано температурное по­ле от подвижных линейных источников теплоты в пластине, дви­
жущихся с различной скоростью irt при постоянной погонной энергии tyn*cj,/vc. Видно, что по мере пропорционального увеличения мощности и скорости источника теплоты изотермы не­сколько расширяются и значительно удлиняются.