Temperature and doping dependence of recombination
 5 марта, 2014
5 марта, 2014  admin
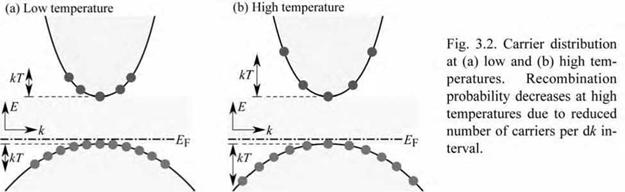
admin The temperature dependence of the recombination probability is elucidated in Fig. 3.2, which shows a parabolic E(k) relationship at low and high temperatures. Inspection of the figure reveals that the number of carriers per dk interval decreases with increasing temperature. As radiative recombination requires momentum conservation and the recombination probability of an electron is proportional to the number of holes available at equal momentum, the recombination probability decreases with increasing temperature. This trend is confirmed by Eqs. (3.24) and (3.25), which display a T 3/2 dependence of the bimolecular recombination coefficient.
The doping-concentration dependence of the recombination probability is elucidated in
|
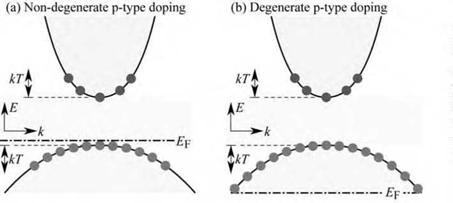
Fig. 3.3, which shows E(k) for non-degenerate and degenerate doping concentrations. Inspection of the figure reveals that the number of holes per dk interval remains constant in the degenerate doping regime. Thus the recombination probability does not increase in the degenerate doping regime.
|
|
|
|
Fig. 3.3. Carrier distribution in (a) non-degenerately and (b) degenerately doped p-type semiconductor. Degenerate doping does not increase the overlap between electrons and holes with equal momentum. |
|
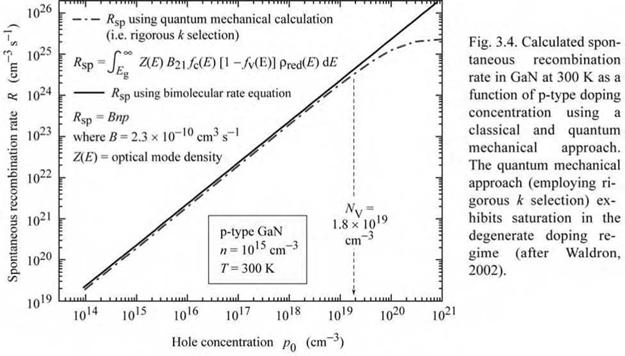
This contention is confirmed by the quantum mechanical calculation of the bimolecular recombination coefficient that is shown versus doping concentration in Fig. 3.4 (Waldron, 2002). Inspection of the figure reveals that the bimolecular recombination coefficient saturates in the degenerate doping regime. The van Roosbroeck-Shockley model does not exhibit this characteristic as its validity is limited to the non-degenerate case. The bimolecular rate equation, R = Bnp, applies to dilute carrier concentrations, i. e. to non - degenerately doped semiconductors. Thus the bimolecular recombination coefficient applies to semiconductors with non-degenerate carrier concentrations. In this case, the bimolecular recombination coefficient is independent of the carrier concentration. For very high carrier concentrations, however, the bimolecular recombination coefficient decreases due to an |
increasing momentum mismatch between electrons and holes. The bimolecular recombination coefficient in the degenerate regime can be expressed as
|
n |
|
B hi |
|
(3.26) |
|
= B - |
|
b- |
|
Nc |
|
high concentrations |
That is, the recombination coefficient is reduced at high concentrations. A detailed discussion of the bimolecular recombination coefficient at high concentrations including numerical values for B* can be found in the literature (Agrawal and Dutta, 1986; Olshansky et al., 1984).
|
|
Exercise: Radiative efficiency. Analyze the temperature dependence of the radiative lifetime based on the van Roosbroeck-Shockley model and the non-radiative lifetime based on the Shockley-Read model and predict the temperature dependence of the radiative efficiency in semiconductors.

 Опубликовано в
Опубликовано в