При выводе основных расчетных уравнений предполагаем, что:

I) жидкость несжимаемая, с произвольной кривой течения

y=/w,

смачивает стенки канала;

2) жидкость высоковязкая, массовыми силами пренебрегаем;

3) процесс изотермический;

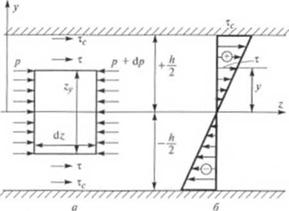
4) влиянием боковых стенок канала пренебрегаем. Предполага­ем также, что давление является функцией только координаты *, I. е., что р = />(*), и поэтому градиент давления dp/d* = const (рис. 1.16, а).

Рассмотрим при этих условиях баланс сил, действующих на • юмент жидкости единичной ширины, толщиной 2у и длиной d* (см. рис. 1.16, а).

Проектируя действующие силы на ось *, получим:

р2у 1 - (p+dp)2y ■ I + 2td* • I = 0.

о I куда

(1.102)

| ле р — давление жидкости; d/>/d* — градиент давления в направлении оси г; А — пысота канала; т — напряжение сдвига в плоскости, перпенликулирной оси у, и направлении оси z.

Рис. 1.16. К анализу процесса течения и плоской неограни­ченной щели

Из уравнения (1.102) следует, что в плоском неограниченной щели напряжение сдвига изменяется линейно по высоте канала (рис. 1.16, б).

Для жидкостей с произвольной кривой течения имеем следую­щее реологическое уравнение:

. dv,

= (1103)

гле v — текущая скорость жидкости.

Интегрированием уравнения (1.103) получим:

v у

fdv= I /(т)<1у. (1 104)

0 /;/ 2

Для ньютоновской жидкости с реологическим уравнением

(1.105)

у = /(т) = т/р

имеем:

1 f А

(1.106)

V = — J T(iy. МА/2

С учетом (1.102) для напряжения сдвига получим следующее выражение для скорости жидкости в плоской неограниченной щели:

Id рУ. 1 dpf

V = —j yxiy = f-

2ц dz

(1.107)

Для жидкости, подчиняющейся степенному закону вязкости, имеем |см. уравнение (1.26)]:

(1.108)

у = /(т)=лг*.

Совместным решением уравнений (1.108) и (1.104), с учетом выражения для напряжения сдвига (1.102), получим:

(1.109)

у -■ - - у т-тт. у dz

v= I /(t)dy = J A/2

*4У A/2 Пр A/2

d y =

Для бингамовских жидкостей г/ т~тт /(т) =-- т - при т>хт; П/> /(т)=0 при Т£ТТ. Из уравнения (1.104) получим: d р

>• Т.-И-'т

Пр

(1110)

J_dp Пр dz

_iH)

Расход жидкостей (производительность) через неограниченную плоскую щель находится интегрированием скорости по попереч­ному сечению рассматриваемого канала:

А/2 Л/2 vyff2- rdv 0

А/2

(1.111)

Q = 2B ( i'dу = 2В 0

• и - // - ширима щели.

Первый член правой части уравнения (1.111) равен нулю, так ».iK при у = /г/2 v = 0 (из условия смачиваемости стенок).

Кроме тою,

dv = /(x)dy (1.112)

|см. уравнение (1.103)|.

Для нахождения выражения дифференциала dy обратимся к рис 1.16, б, на котором представлен график изменения напряже­ния сдвига по высоте канала, откуда следует (из подобия треуголь­ников), что

У _ т

Л/2

где тс - напряжение сдвига на стенках канала.

Из последнего выражения получим:

А ^,С, Т

Ь= 2~- (1.114)

С учетом выражений (1.112) и (1.114) уравнение (1.111) приво­дится к следующему виду:

„ I В/г2 'с в/i2 . .

Qs~7~T I TAT)dT = "TT 1 ^<T)dT - (1.115)

1 о 2 Тс О

Для ньютоновских жидкостей_/(т) = т/р. т. с.

„ В/r г. с т2 , /?Л2 тс

2т? о7 “"и’ <1116>

или с учетом, что

d р И

Tc = dT2- С"7)

окончательно получим:

^ в/i1, dP

В случае течения через плоскую щель степенной жидкости, для которой Дт) = схт*. из уравнения (1.115) следует:

„ B/r's i +1 . а В/г T*t2 aBhk+2 (6р к

2т2 о Т 2т2 * + 2 (* + 2).2*+l(d*J <1||9)

Для каналов постоянных размеров при стационарном течении можно принять, что

d р Лр

dF T

Тогда из уравнения (1.119) получим:

п aBhk*2 рк

где Др - перепад дапления в плоской шелн.

Для бингамовской жидкости, для которой/(т)® (т - т7)/пР. при « * тт А*) = 0, при т £ тт из уравнения (1.115) получим:

-я

/ т/(т)с! т+/V(T)dr. (1.121)

° tr

Первый член правой части уравнения (1.121 )равеп нулю, так как Дт) = 0 при т < т, 17|.

Поэтому

		>	3	/
B/r dp	ч		3	Ь
12г)р d^	dp h 1^5 J	2	dp h [55j

.. В/г I с, 2 V В/г Q = = f (т - ттт }dr = =—

2тс П/,т. ' 2тспр

1.8.2. ТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ЦИЛИНДРИЧЕСКИЕ КАНАЛЫ

3

Тг Тт тгтг т.

(1.122)

При общепринятых допущениях в отношении ньютоновской * ид кости (и зотермичность и ламинарность процесса, прснебре - кснис массовыми и инерционными силами, несжимаемость жид­кости, смачиваемость стенки) из рассмотрения баланса сил, дей­ствующих на элемент жидкости толщиной dr и длиной d* (см. рис. I 17), получим:

.2 . л л. /„.л„_..2

ркг - + 2nrxdz~(р + dр)пг - О,

«»I куда

(1.123)

d р г

T"dz2’

ml - г — текущий радиус.

При г = R из уравнения (1.123) получим выражение для напря­

жения сдвига на стенке канала:

(1.124)

dp R

dc 2

ml - R — радиус канала.

Графическая иллюстрация уравнения (1.124) представлена на рис. 1.17. Из него следует, что:

(1125) 53

т/т с =г/К.

Рис. 1.17. К апашiv процесса течения в iih пшаричеекпм канале

откуда

r~~R - (1.126)

Для жидкостей с произвольной кривой течения имеем следую­щее реологическое уравнение:

dv v

Y_d7=/(T)' <1|27>

которое при интегрировании дает:

fdv=J/(x)dr. (1 128)

о к

Откуда для ньютоновской жидкости [см. уравнение (1.105)) скорость потока в цилиндрическом канале равна

v^[ldr (1.129)

С учетом уравнения (1.123) получим:

v2

(1.130)

-TTr2 4м d z

откуда следует, что распределение скорости для ньютоновской жидкости при напорном ее течении в цилиндрическом канале яв­ляется квадратной функцией от радиуса R.

Для степенной жидкости (см. уравнение (1.108>| с учетом выра­жения (1.123) из уравнения (1.128) следует:

A+l

1 (d/Л* Я**1

(1.131)

d г = ~

a(A' + l)(d^J 2

Для бингамовской жидкости, реологическое уравнение кото­рой описывается формулой (1.24), имеем: г d р

v = (1132)

И Пр R Пр Пр ^Пр

Выражение для расхода жидкостей через круглый канал нахо - iiiM путем интегрирования скорости потока по поперечному сечс - ншо канала:

R R?

Q = j v2nrdr = тт J vdr = л vr" о о

(1.133)

Первый член правой части уравнения (1.133), из условия сма­чиваемости, равен нулю.

Из уравнения (1.127) получим, что

dv = /(x)dr, (1.134)

a dr находится дифференцированием уравнения (1.126):

(1.135)

dr = —dx.

тс

Гогда из уравнения (1.133) получим:

(1.136)

(?=-^T2/(x)dt.

4 О

Для ньютоновской жидкости с учетом ее реологического урав­нения из выражения (1.136) следует:

(1.137)

я/?3т:? •> х. л Я4 dp (? = “Г—ОХ-—-—f.

х3 О й d*

( учетом, что в цилиндрическом канале постоянного размера d/i/d* = tap/L, уравнение расхода для ньютоновской жидкости при­мет вид (уравнение Пуазейля):

0-t~L' <М38)

и р— перепал давления на длине I. цилиндрического канала.

Для жидкости, подчиняющейся степенному закону (1.108), из уравнения (1.136) получим:

TOC o "1-5" h z п я/?3 т. с 2 к « яд/?3 х£'3

Q = —Г / х дх dx =----------- =

X3 о X3 Л + 3

(1.139)

лаЯ**3 Г dpt тмЯ*’3 j'Ap4*

2‘(*+3)[<fcJ 2*(* + 3)t i

При A = 1 уравнение (1.139) превращается в уравнение Пуазсй - ля (1.138).

Для бингамовской жидкости с реологическим уравнением, описываемым формулами (1.108) и (1.136), имеем:

kR

Q

(1.140)

Тс

J* t2/(T)dT + TJ T2/(t)di 0 Тт

Первый член правой части уравнения (1.140) равен нулю, так как при х < хт Дх) = 0. С учетом этого из данного выражения получим:

1х

'-Т

(1.141)

,, л/?3 V 2/ i я/? тс Т, 4т1р

Расход бингамовской жидкости через круглую трубу можно представить и через перепад давления, заменив для этого напря­жение сдвига на стенке следующим его выражением:

ДpR