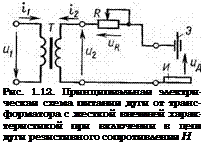Особенности горения дуги переменного тока. Условия существо­вания дуги при ее питании от источника переменного тока, напри­мер от трансформатора с синусоидальным напряжением, отличают­ся от условий ее существования при питании постоянным током. При синусоидальном напряжении частоты 50 Гц активное пятно на катоде сто раз в секунду изменя­ет свое расположение. К концу каждого полупериода синусои­дальное напряжение уменьшается до нуля; при этом уменьшается напряженность электрического поля разрядного промежутка.

Вследствие этого уменьшается степень ионизации газа в столбе дуги, рассасывается пространст­венный объемный заряд в при - электродных областях и уменьшаются напряженности электриче­ского поля Ек и Е3. Все это ухудшает условия Поддержания ста­бильного дугового разряда.

На рис. 1.12 приведена принципиальная электрическая схема питания дуги от источника переменного тока. Источник состоит из однофазного понижающего трансформатора Т с ничтожно малой индуктивностью обмоток, обладающего жесткой внешней характе­ристикой, и регулятора тока R, представляющего собой регулируе­мое линейное резистивное сопротивление. Резистор формирует внешнюю падающую характеристику источника и служит для регу­лирования сварочного тока.

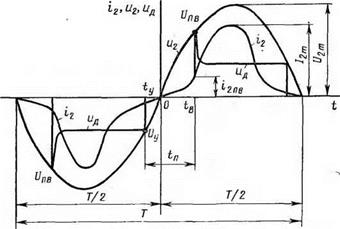
Графики изменений во времени мгновенных значений вторичного напряжения щ трансформатора, сварочного тока t2 и напряжения на дуге цд приведены на рис. 1.13, (Для большей наглядности вели­чины тока i2 и соответствующие им отрезки времени на рисунке сильно увеличены.) Графики представляют собой осциллограммы, полученные светолучевым осциллографом. Напряжение и ток запи­
саны в отрицательный и положительный полупериоды синусоидаль­ного напряжения «2- Ток h и напряжение на дуге ил несинусоидаль­ны. Последнее объясняется тем, что нагрузкой трансформатора является нелинейная среда разрядного промежутка, проводимость которого зависит от величины тока /г дуги. При наличии в сварочном контуре только резистивного сопротивления максимумы и нулевые значения i2 и ц2 совпадают во времени. В отрицательный полупери - ■од при t=ty, когда синусоидальное напряжение уменьшается до зна­чения t/д, недостаточного для создания между изделием и электро­дом напряженности электрического поля, необходимой для сущест­вования дугового разряда, последний практически угасает. До t=tB

Рис. 1.13. Графики изменений во времени мгновенных значе­ний вторичного напряжения «2 трансформатора, сварочного тока /2 и напряжения на дуге ил

в положительный полупериод ток Ї2 практически равен нулю. Интер­вал времени от t—ty до t=tB называют временем перерыва tn в горе­нии сварочной дуги. По осциллограмме (рис. 1.13), однако, видно, что в течение времени tn ток i2 в сварочном контуре не равне нулю. Осциллограф фиксирует наличие тока i2, т. е. то, что проводимость участка цепи между изделием и электродом не равна нулю. Наличие проводимости G разрядного промежутка обусловливается проводи­мостью плазмы и эмиссионной способностью нагретых электродов. Однако в течение времени tu электрический разряд является неду­говым разрядом. В следующий полупериод, когда синусоидальное напряжение и2 начинает возрастать от нуля и достигает значения U2—Uu_B, в момент t=tB вновь создаются условия для существова­ния дугового разряда и дуга повторно возбуждается. Напряжение UB. B, называемое напряжением повторного возбуждения дуги, за­висит от многих факторов и прежде всего от физико-химических •свойств среды между изделием и электродом. Когда и2 в момент времени tB становится равным Un. B, в дуговом промежутке обеспе­чивается напряженность электрического поля такой величины, при которой возможны интенсивное зарождение свободных электронов и восстановление условий для существования самостоятельного дугового разряда. Возбуждение дуги после перехода и2 через нуль произойдет, как только будет создана требуемая напряженность электрического поля в дуговом промежутке.

Из рассмотренного можно сделать вывод, что при наличии в сва­рочном контуре только резистивного сопротивления в течение вре­мени tn дуговой разряд отсутствует — дуга угасает. Следовательно, в этих условиях наблюдается нестабильность процесса сварки. Ве­личина тока i2 электрического разряда и скорость изменения тока di2/dt при смене полярности незначительны. Можно считать, что в течение времени tu сварочный контур практически разомкнут. По исследованиям [11] величина тока i2 при t=tB составляет 1—2% от действующего значения тока i2. После повторного возбуждения дуги начиная с t=tB ток i2 и di2/cU резко возрастают.

Для уменьшения времени перерыва tn в горении дуги и увеличе­нии dt2/d/ при смене полярности можно идти двумя путями: умень­шать 1/п. в, изменяя физико-химические свойства среды между элект­родом и изделием, или изменять свойства источника питания. Un. B можно уменьшить, вводя в парогазовую среду между электродом и изделием химические элементы с низкими потенциалами иониза­ции. Это можно осуществить путем покрытия стержневых электро­дов слоем, содержащим требуемые элементы, а при механизирован­ной сварке вводить их в состав флюса или в состав фитиля, нахо­дящегося внутри ПОЛОЙ электродной проволоки. Снижение Un. B можно осуществить также, снижая давление среды.

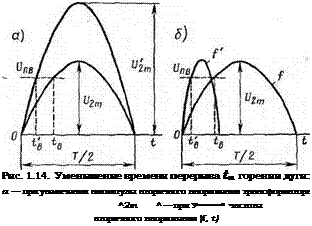
При том. же значении Un. в время перерыва tn в горении дуги можно уменьшить за счет увеличения амплитудного значения нап­ряжения и2 трансформатора. На рис. 1.14, а видно, что при увеличе­нии U2m трансформатора дуга повторно возбуждается в момент t'B, благодаря чему уменьшается^.

Величина отношения ]/2U2K_xfUA=n, где £/гх. х— действующее значение напряжения холостого хода, зависит от способа сварки и физико-химических свойств среды. Как показывают исследования [11], 2-7-4. Однако увеличение U2m, а следовательно, и £/2х. х ог­

раничено не только технико-экономическими показателями (увели­чивается сечение сердечника, растет расход обмоточных материалов трансформатора), но в первую очередь условиями безопасности при выполнении сварочных работ. Исходя из этого, желательно не уве-- личение, а уменьшение 1/2х. х-

Из рис. 1.14, б. видно, что уменьшить tu можно увеличением час­тоты напряжения и2. При f'>f (f=50 Гц) дуга повторно возбуж­дается при tB <tB. Экспериментально установлено оптимальное значение частоты: наиболее устойчиво горит дуга при частоте

f'= (5—9)f. Следует отметить, что сварочная дуга повышенной час­тоты издает резкий звенящий звук и неблагоприятно воздействует на сварщика!

Облегчить повторное возбуждение дуги переменного тока мож­но применением специальных устройств — осцилляторов и импуль­сных возбудителей. На практике питание дуги переменным током при ручной дуговой сварке в атмосфере воздуха плавящимся элек-

тродом и при сварке под флюсом осуществляют, включая в цепь дуги не резистор, а катушку с ферромагнитным сердечником, обла­дающую значительной индуктивностью, или осуществляют питание

дуги от трансформатора, об­мотки которого обладают большой индуктивностью.

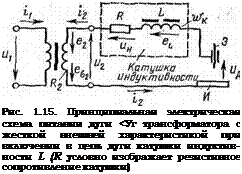
Устойчивость горения сварочной дуги при включе - нии в сварочный контур ли­нейной индуктивности. Прин­ципиальная электрическая схема источника питания ду­ги переменным током с ка­тушкой индуктивности в сва­рочном контуре приведена на рис. 1.15. Катушка обла­дает индуктивностью L и ре-, зистивным сопротивлением R. Для облегчения анализа процессов, происходящих в схеме, при­мем, что цепь линейная. Дуга замещена линейным резистивным со­противлением /?д. На схеме е2— вторичная э. д. с. трансформатора; ео2— э. д.с. рассеяния вторичной обмотки; R2— резистивное сопро­тивление этой обмотки.

При прохождении сварочного тока i2 по обмотке катушки ин­дуктивности магнитодвижущая сила wK i2 возбуждает в сер­дечнике катушки изменяющееся во времени магнитное поле, кото­
рое индуктирует В обмотке Э. Д.С. самоиндукции еL. По второму правилу Кирхгофа можно составить уравнение для сварочного кон­тура, обходя его по направлению тока /2

Ид-1-/?2*2'Ь^?*2» (1.22)

где ид — мгновенное значение напряжения на дуге.

Если дуга горит устойчиво, то напряжение ид можно считать постоянным и равным Va. Кроме того, в (1.22) R2I2 пренебрежимо мало по сравнению с э. д.с е2, т. е. |/?2^21 |иг|. Примем, что сва-

рочный ток 1*2=/2т sin G)t, т. е. начальная фаза тока фч=0. Тогда 42= и2т sin (<й/ - Kf2), где ф2 —УГОЛ СДВИГЭ МЄЖДУ П2 И І2

При Rz^Xl и X2<iXL величинами резистивного и индуктивного со­противлений вторичной обмотки трансформатора по сравнению с xL можно пренебречь и тогда из (1.22) при сделанных допущениях получим линейное уравнение

Щг=и(Е24)

где uL — — eL=Ld i2/d t=xLl2m sin (ш/-j- jt/2).

Подставив вместо и2 и иь их выражения, записанные выше в (1.24), получим

^2m sin (<ot-]-<p2) — Uд-j--*)/2т Sin(lD/-f я/2). (1.25)

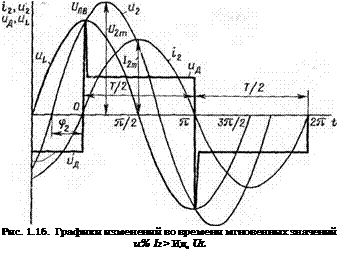
На рис. 1.16 приведены графики изменений во времени мгновен­ных значений И2, /2, Ид И Их,.

В окрестности значения тока i2—0 остаточная проводимость плазмы в дуговом промежутке чрезвычайно мала. Можно считать, что разрядный промежуток после угасания дуги практически разом­кнут. Из (1.25) при t—О имеем

U2m sin ъ=хь12т.

Напряжение, подведенное к разрядному промежутку, представ ляет собой алгебраическую сумму двух э. д.с. е2 и вь-

йд—e2--eL.

Когда ток i2 при смене полярности, пройдя нуль, возрастает, то в магнитном поле индуктивности L накапливается энергия. В дальнейшем при уменьшении синусоидального напряжения иг. ток Ї2 также уменьшается, спад магнитного поля в сердечнике ка­тушки вызывает появление в ее обмотке э. д.с. самоиндукции вь, которая, складываясь с убывающим по абсолютной величине на­пряжением и2, поддерживает разность потенциалов на разрядном промежутке. Благодаря этому поддерживается напряженность электрического поля в межэлектродном промежутке, необходимая для существования тока i2.

При уменьшении напряжения и2 трансформатора до нуля про­цесс сварки производится за счет запасенной энергии магнитного поля катушки, так как при и2, близком к нулю и равном нулю, энергия от сети в зону сварки не поступает. Кривая тока практиче­ски синусоидальна. Ток i2 отстает по фазе от и2 на угол <р2, опреде­ляемый соотношением индуктивного и резистивного сопротивлений сварочного контура. Важно отметить, что при сделанных допуще­ниях величина u2—U2msn($2 не может быть больше амплитудного значения Uгт - Чтобы дуга горела устойчиво и /п->-0, значение и2= — sin ф2 должно быть не меньше величины напряжения повтор­ного возбуждения дуги Un. в. При данном действующем значении тока /2 величина u2=U2msinq2 определяется величиной хь = ч>Ь. Ток i2 в рассматриваемых условиях при наличии в цепи дуги индук­тивности L имеет синусоидальную форму и tn практически равно нулю.

Порядок величины угла ф2 между и2 и i2 можно определить для •конкретного способа сварки, пользуясь опытными данными для со­отношения между величинами - ^2х. х=^2m/V2 и напряжения

t/д при устойчивом горении дуги. В [11] приводится соотношение для ручной дуговой сварки плавящимся электродом

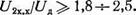(1.28)

Используя (1.24) и (1.25), пренебрегая падением напряжения от R сварочного контура, можно определить порядок величины угла <р2, создаваемого за счет включения последовательно с дугой ин­дуктивности L. С учетом (1.24) получаем

(1.29)

Интегрируя (1.29), находим, что

где A = Uim cos <р2/ (шL) — постоянная интегрирования;

h = -^~-j^Cos ?2 — COS H + <Ы--------------------------- ,

При (ot = n TOK І2 = 0, что дает возможность определить из фор­мулы (1.30) cosjp2. После несложных преобразований оказывается, что cos<p2=l/2jt/(2«), где п—ІІ2і. х/иа. Если принять я«2 пэ (1,28), то cos ф2=0,56, что соответствует <р2=55° и соотношению XlIRr=§. Таким образом, для известного способа сварки и при из­вестных соотношениях П21.х/С/д можно полу­чить данные для подбора величины индук­тивности сварочного контура по соотноше­нию xL/Ra.

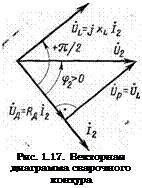
Условие устойчивого горения дуги пере­менного тока при включенной последова­тельно с дугой индуктивностью можно сфор- мулировать-Л’аким образом: амплитуда па­дения напряжения на индуктивности xLhn должна быть не меньше напряжения повтор­ного возбуждения С/П. в дуги для данного спо­соба сварки. При анализе явлений, протека­ющих в сварочном контуре, предполагалось, что цепь линейна, индуктивность цепи L не зависит от величины тока цепи, а дуга бы­ла замещена линейным резистивным сопро­тивлением. Ток i2 был принят синусоидальным. При этих допуще­ниях можно построить векторную диаграмму сварочного контура (рис. 1.17).

В реальных условиях сварки разрядный промежуток является нелинейной средой, и его проводимость G зависит не только от величины тока, но и от целого ряда физико-химических факторов, о чем говорилось выше. При исследовании процессов, происходя­щих в нелинейных цепях электротехнических устройств, когда ана­литическое решение нелинейных дифференциальных уравнений, описывающих эти процессы, затруднительно, то прибегают к каче­ственному исследованию процессов с помощью фазовой плоско­сти [2].

Фазовой плоскостью называют плоскость, по оси абсцисс кото­рой откладывается исследуемая величина, например сварочный ток І2, а по оси ординат — его производная di2/df. Любому сочета­нию i2 и dt2/"d/ сварочной цепи соответствует вполне определенная так называемая изображающая точка y4(di2/dtf, i2) на фазовой плоскости. Для получения фазовой траектории на горизонтальные отклоняющие пластины светолучевого осциллографа подводится

напряжение, пропорциональное изменению тока i2, а на вертикаль­ные — напряжение, пропорциональное di2/dt. Это напряжение по­дается с дифференцирующего контура, обладающего малой посто­янной времени. Фазовая траектория является интегральной кривой и соответствует заданным начальным условиям. Если исследуемый процесс периодический, то фазовая траектория является замкнутой кривой. Скорость изменения сварочного тока при его переходе че­рез нуль, а следовательно, и форма фазовой траектории зависят как от физико-химических свойств среды между изделием и элект­родом, так и от свойств источника питания.

Легко показать, что фазовой траекторией синусоидального про­цесса в линейной электрической цепи является эллипс (рис. 1.18). Действительно если принять начальную фазу сварочного тока рав­ной нулю, то для тока и его производной можно записать i2 = = /2msin(o^ и di2/d^ = co/2TOcos со< и, преобразовав, получить sinto£=

= І2ІІ2т, costot= Имея В ВИДу, ЧТО Sin2 0)f + COS2 tot = 1, ПО-

«/2 m

лучим уравнение эллипса в координатах (i2, di2jdt):

(_h _2 і / d i2id t 2_ j [ hm ) «/2m /

Вернувшись несколько выше, получим при ^=0 sinco< = 0, i2=0, costo^=l, di2/d< = co/2,„, а при t=nj2 sinto^=l, i2=hm, costo^=0,

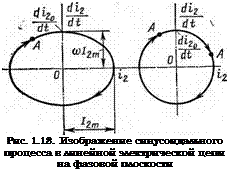di2/d£=0. Расположение эллип­са на фазовой плоскости зави­сит от начальных условий. Вы­бором масштабов по осям фа­зовой плоскости можно свести эллипс к окружности. Градуи­рование осей производят при записи di2/dt и i2 в режиме ко­роткого замыкания сварочного контура, когда G=оо (исклю­чен нелинейный участок цепи дуга — ванна).

В реальных условиях, ког­да 0<G<oo, происходит иска­жение фазовой траектории по сравнению с окружностью. По форме фазовой траектории можно судить об устойчивости горения сварочной дуги переменного тока в данных конкретных условиях, т. е. объективно оценивать техно­логические свойства энергетической системы источник питания — дуга — ванна при сварке переменным током (см. гл. 6). Если фа­зовая траектория тока г2 представляет собой незамкнутую кривую, то это свидетельствует о перерывах в горении дуги. В реальных условиях сварки фазовая траектория отличается от окружности; это объясняется тем, что контур источник питания — дуга — ванна является нелинейным. Фазовая траектория тока i2 несимметрична относительно осей.

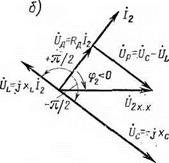
Устойчивость горения сварочной дуги при включении в свароч­ный контур индуктивности и емкости. При включении в сварочный контур катушки индуктивности с ферромагнитным сердечником L и батареи конденсаторов С (рис. 1.19) устойчивость дуги перемен­ного тока при определенном соотношении сопротивлений Хь и хс повышается. Будем считать, что иследуемая цепь линейна. Тогда возможно использование векторных диаграмм и комп­лексных функций, что суще­ственно упрощает анализ це­пи и делает результаты бо­лее наглядными. Вычислив XL и Хс, требуется их величи­ны уточнить в реальных ус­ловиях сварки путем записи фазовой траектории свароч­ного тока i2. Характер про­текающих процессов и устой­чивость горения дуги зави­сят от соотношения XL И Хс - Когда xL>Xc, ток t2 отстает от выгодного напряжения «2 трансформатора: и2=

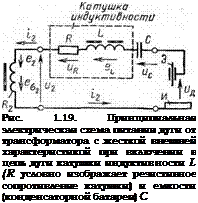
=.C/2msin (coN-фг), так как i'2=^2mSin (начальная фаза тока фг=0); если xL<хс, то и2 = H2msin(со/—<р2).

Уравнение для сварочного контура источника

u2 = U(1-31)

где wc = xc/2TOsin(co(—я/2); uL=—eL=xLI2m sin (со/+я/2); мн = —RI2m sin Сot.

В реальных сварочных цепях всегда |пн| значительно меньше иь, ис и С/д. При (=0, когда /г=0, напряжение ис на конден­саторной батарее равно амплитудному значению

U-c= —(1*32)

Из (1.31) и (1.32) следует, что как при xL>Xc, так и при Хь<хс мгновенное значение и2 равно xLhm - Дуга повторно возбуждается, если мгновенное значение напряжения источника будет не меньше напряжения повторного возбуждения ии. в дуги. Отсюда понятна роль емкости в цепи дуги. Чем больше ис, тем при меньшем значе­нии u2 = U2m sin ф2 дуга возбуждается после перехода тока г'2 через нуль. На рис. 1.20 приведены векторные диаграммы, построенные, как уже говорилось, в предположении, что проводимость разряд­ного промежутка не зависит от тока.

Анализ процессов, происходящих в цепи дуги, с использованием линейных уравнений носит лишь качественный характер. Величины L и С, определенные аналитическим путем, как сказано выше, тре­буют уточнений с использованием метода фазовой траектории.

Использованием энергии, накапливаемой в магнитном поле ин­
дуктивности и в электрическом поле емкости, удается создать ус­ловия для легкого повторного возбуждения дуги переменного тока промышленной частоты без применения специальных устройств (осцилляторов, импульсных возбудителей). Наличие в цепи дуги переменного тока не только индуктивности, но и емкости при их вполне определенных для данного способа сварки величинах позво­ляет снизить напряжение холостого хода трансформатора, что имеет экономическое и эксплуатационное значение. Описание

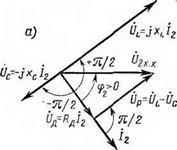свойств источника переменного тока промышленной частоты с Хь и Хс в цепи дуги приведено в гл. 6.

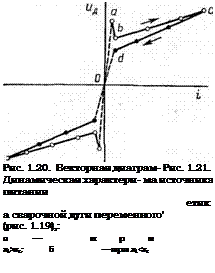
Динамическая характеристика сварочной дуги переменного тока. При исследовании свойств свароч­ных дуг переменного тока, горящих в разных физико-химических усло­виях при различных способах свар­ки, пользуются их динамической ха­рактеристикой, которая представля­ет собой зависимость между мгно-

венными значениями ип и сварочного тока, построенную по данным осциллограмм, полученных на светолучевом осциллографе. На рис. 1.21 приведена динамическая характеристика дуги, горящей в атмосфере воздуха при ручной дуговой сварке. Характеристика имеет две расходящиеся ветви: восходящую Ъс и нисходящую cd> полученные при возрастании и убывании тока (показано стрелка­ми). Заметное расхождение этих ветвей наблюдается у дуги, го­рящей в среде, содержащей примеси паров легко ионизирующихся элементов (калия, кальция, натрия), а также у дуг, горящих в средах с высокими потенциалами ионизации, с ростом частоты на­пряжения, питающего дугу. Расхождение ветвей больше при свар­

ке меньшими токами. Часть ветвей динамической характеристики для двух полупериодов на рис. 1.21 показана пунктиром (оа и do). Эти части ветвей соответствуют преддуговому состоянию межэлек­тродного пространства и не улавливаются светолучевым осцилло­графом. Нарушение устойчивости в горении дуги при малых зна­чениях dijdt при смене полярности приводит к нестабильному про­цессу сварки, что отрицательно отражается на качестве сварного шва.