Статической характеристикой преобразователя будем называть зависимость среднего тока в сопротивлении Ra от частоты входного сигнала. Как следует из выражения (6), средний ток линейно зави­сит от f AU при С = const. Величина AU представляет собой разность уровней напряжений, между которыми перезаряжается конденсатор.

В рассматриваемых преобразователях суммарное время переза­рядки конденсатора ограничено периодом преобразуемого сигнала, т, е.

+ 1/f,

где /3 — время зарядки; /р — время разрядки.

Заряд и разряд конденсатора С їв этих схемах осуществляется по разным цепям с постоянными времени: т3 — цепи зарядки, тр — цепи разрядки.

Величина AU в схеме, изображенной на рис, 1, практически не зависит от частоты следования импульсов, если

Тр^/р.

Когда последние соотношения не выполняются, величина AU и, следовательно, средний ток /ср зависят от частоты.

Исследуем эту зависимость более-подробно для некоторых схем. Определим статическую 'характеристику преобразователя с до­зирующим устройством, приведенным на рис. 3,а.

Дифференциальное уравнение процесса зарядки конденсатора Сі имеет вид:

du£

Ек = /в„«к + С, К„ + "сз, (7)

і

где Мез — напряжение на конденсаторе іво время зарядки; /ко— ну­левой ток коллектора (закрытый транзистор рассматривается как источник тока /ко):

В результате решения уравнения (7) получаем:

Uq3 = Ne 3 Ек — IkqRk*

где N — постоянная интегрирования; т3 = /?кСі — постоянная времени цепи заряда.

Дифференциальное уравнение разряда конденсатора имеет вид:

diicn

% иср СА dt — мкв, (В)

где иср — напряжение на конденсаторе во время разряда; ика — на­пряжение коллектор — эмиттер открытого до насыщения транзи­стора.

В уравнении (8) открытый (до насыщения) транзистор рассма­тривается как источник напряжения икэ. Реальный транзистор при больших токах базы может рассматриваться как последовательное соединение генератора напряжения и*кэ и линейного сопротивления Ядоб, т. е. u*k9=u*k+IkRp, o6. Как показали экспериментальные ис­следования [J1. 2], величина /?доб для ряда германиевых транзисто­ров колеблется от 1 до 3 ом и может не учитываться при расчете. Решая уравнение (8), получаем:

t_

«ср = “кэ + Fe Р -

где F — постоянная интегрирования;

Тр=і? иСі — постоянная времени разряда.

Так каїк 'Процессы зарядки и разрядки конденсатора следуют друг за другом непрерывно, то оказывается, что напряжение иср в конце разрядки равно напряжению ис з в начале зарядки и на­оборот.

Из этих условий определяются постоянные интегрирования N

и F.

Исходя из этого, получаем:

-Is.

Fe “Ь ^кэ ~ N + Ек — Л oRk

К

Fи-къ — Ne - J - Ек — IvqRh-

N — {Ек — I vqRk — Uvq)

Из выражения (12) следует, что величина Аис зависит от ча-
стоты входного сигнала. А так как

/ср=/СА£/с,

то второй сомножитель в выражении (12) определяет отклонение
от линейности зависимости среднего тока от частоты.

Практически удобней использовать преобразователи с линейной статической характеристикой. Поэтому реальная характеристика линеаризуется. При линеаризации характеристики прибора возникает погрешность нелинейности, зависящая от способа линейной аппроксимации статической характеристики. Выбор того или иного способа аппроксимации определяется конкретными условиями задачи, стоящей перед конструктором. Ниже приводится определение погрешности нелинейности для одного из способов линеаризации. Относительная величина отклонения статической характеристики от линейности определяется выражением

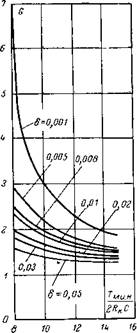
Анализ выражения (13) показывает, что при Г> т3 и Г» тр величина 6i стремится к нулю. Зависимость величины 6i от отношения Г/т при T3 = tp = T приведена на рис. 9. Таким образом, статическая характеристика однотактного пре образователя без фильтра (рис. 3,а) имеет вид:

Icp = fC(EK-IK0RK-UKd) (1-Si). 014)

Величина среднего тока /ср для схемы, приведенной на рис. 3,6, может быть получена при допущении, что временем разряда конденсатора можно пренебречь, так как цепь разряда емкости С (см. рис. 3,6) состоит из диода и открытого до насыщения триода. При этом AUс — (Ек IkqRk—Г)кэ) (1—6и), (15)

Где схем рис. 3д и б видно, что схема, приведенная на рис. 3,6, имеет более линейную характеристику при т3=тр=т. При эгом величина максимальной погрешности нелинейности при способе аппроксима­ции, указанном в приложении, может быть определена по формуле

-2/макс тз 1п 2

Статическая характеристика двухтактных схем имеет вид:

/ср = 27С(£к-/ко*к-*/иэ) (1-6). (17)

Выражение отклонения от линейности статической характери­стики двухтактных схем, приведенных па рис. 5 и 7,а, совпадает с формулой (13). Так как для схемы рис. 7,а принципиально необхо­димо, чтобы т3 было больше Тр, а схему рис. 5 можно построить с t3<Tp, то при прочих равных условиях схема, приведенная на рис. 5, 'имеет более линейную статическую характеристику. При по­лучении зависимости среднего тока от f было принято, что диоды идеальны. Нелинейность вольт-амперной характеристики диодов влияет на линейность статической характеристики преобразователя. В большей степени неидеальные свойства диодов сказываются на работе устройства, показанного на рис. 7,и, где в цепях зарядки и разрядки последовательно включены по два диода.

Выражение, определяющее отклонение статической характери­стики от линейной для двухтактной двухъемкостной схемы (рис. 8), совпадает с формулой (17). При проектировании этой схемы сле­дует учитывать повышенные требования к фронтам управляющих импульсов, так как возможно состояние, при котором транзисторы Ті и Г2, например, уже открылись, а Г3 и Г4 еще не закрылись.

Важной характеристикой приведенных схем является величина мощности на (выходе дозирующего блока. Так как средний ток на выходе схемы не зависит при заданном б от величины /?и, то вели­чина максимального значения Rn определит мощность выхода. Срав­ним схемы, приведенные на рис. 3,а и б.

Сравнение схем выполнено при минимальном периоде повторе­ния импульсов Тмин, так как при этом зависимость среднего тока /Ср от частоты максимально отличается от линейной, что соответствует более не­благоприятным условиям.

На рис. 10 приведены графики за­висимости G от 6 при различных Гмин/2/?кС. Эти данные позволяют сде­лать вывод, что по величине мощности на выходе дозирующего блока при при­нятых в широких пределах значениях отклонения от линейности схема на рис.

3,а является более приемлемой, так как обеспечивает большую мощность выхо­да при заданном отклонении от линей­ности.

Статическая характеристика преоб­разователя зависит от стабильности па­раметров элементов схемы. Одним из наиболее существенных факторов, влия­ющих на параметры схем, является из­менение температуры окружающей сре­ды. При использовании в схеме темпе­ратурно-стабильных сопротивления Як и конденсатора С погрешность обуслов­ливается транзистором и диодами. Тем­пературная погрешность, вносимая тран­зистором, определяется изменением ну­левого тока коллектора /ко и напряже­ния Uкэ при изменении температуры.

Зависимости UKQ = f(t°C) и /ко ={(t°С) могут быть получены по изве­стным соотношениям {JI. 1].

На основании этих исходных дан­ных .может быть определена относитель­ная температурная погрешность по сле­дующей формуле:

значение напряжения коллектор — эмиттер открытого до насыщения транзистора при заданной температуре.

Из ляет уменьшить относительную температурную погрешность преоб­разования, так как величины /ко и UKэ у высоковольтных транзи­сторов существенно не превышают' соответствующие параметры низ­ковольтных транзисторов.

Следовательно относительный уход нулевого коллекторного тока Iко и напряжения между коллектором и эмиттерам при отсутствии коллекторного тока 0КЭ, приведенный к единице коллекторного на­пряжения, сокращается почти пропорционально повышению коллек­торного напряжения.

Относительная температурная погрешность триодов еще более сокращается в случае применения кремниевых транзисторов. Изве­стен ряд схемных решений, позволяющих в большей или меньшей степени скомпенсировать коллекторный нулевой ток транзистора. Все эти решения основаны на применении диодов, изготовленных из того же. материала, что и транзистор, включаемых в обратном направлении так, что их обратная проводимость, увеличиваясь с тем­пературой, вызывает увеличение тока утечки, который компенсирует ТОК Iко.

Указанная компенсация практически осуществляется путем алге­браического сложения на каком-либо из основных резисторов, вхо­дящих в схему транзисторной ступени, тока утечки и тока /ко - Однако все сказанное, может быть применено только для качествен­ной оценки соотношений UKQ = f(t°) и IKo=f(t°). Что касается по­строения указанных функций в реальных масштабах, пригодных для расчета цепей конкретных транзисторов, то следует сказать, что такие функции могут быть построены для каждого типа транзисто­ра на основе исходных данных, полученных экспериментально.

Как показали экспериментальные исследования |[Л. 4], для тран­зистора П26 изменение UKэ равно в среднем 2 мв на 10° С при /к^50 ма и 2—4 мв на 10° С при 50 ма^1к^ 150 ма.

Изложенное позволяет сделать вывод, что при заданном частот­ном диапазоне дозирующий блок может быть рассчитан таким об­разом, чтобы погрешность нелинейности и температурная погреш­ность не превышали допустимых величин.

Стабилизация статической характеристики преобразователя мо­жет быть осуществлена путем включения 'в схему параллельно клю­чу-транзистору стабилитрона.

При включении стабилитрона стабилизируется максимальное значение напряжения на конденсаторе UMакс. Тем самым исключает­ся влияние изменения /ко и Ек на величину UU&KC и, кроме того, существенно уменьшается время заряда конденсатора. Последнее практически ограничивается моментом пробоя стабилитрона.

Включение в схему стабилитрона требует наличия определен­ного уровня напряжения питания схемы Ек. При недостаточной ве­личине Ек для обеспечения нормальной работы схемы в цепь RK можно ввести дроссель, который обеспечит в момент коммутации появление на коллекторе ключа-транзистора UK>EK и UK>Uст. Здесь Uст — напряжение стабилизации стабилитрона.

Остаточное напряжение U кэ на открытом транзисторе может быть уменьшено путем использования специальных приборов (сим­метричных транзисторов, планарных транзисторов) или путем использования соединений транзисторов в схему компенсированных ключей. Напряжение на диодах £/д может быть частично компенси­ровано путем встречного включения диода, шунтированного низко - омным дросселем.