СТАЦИОНАРНАЯ ТЕОРИЯ ТЕПЛОВОГО САМОВОСПЛАМЕНЕНИЯ
 8 апреля, 2013
8 апреля, 2013  admin
admin Рассмотрим химическую реакцию в горючей смеси, заключенной
В сосуд при постепенном повышении температуры окружающей его
Среды, а вместе с ней и температуры горючей смеси. При некоторой
Температуре смеси скорость реакции становится заметной и далее все
|
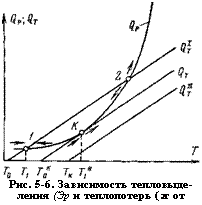
Рис. 5-6. Зависимость тепловыделения (Эр и теплопотерь (2т от температуры. |
 Более увеличивается, соответственно увеличивается количество выделяющегося тепла, что приводит к дальнейшему более резкому повышению температуры смеси. Под действием появляющейся таким образом разности между температурой смеси и температурой среды возникают тепловые потери из реакционного объема в окружающую среду, которые
Более увеличивается, соответственно увеличивается количество выделяющегося тепла, что приводит к дальнейшему более резкому повышению температуры смеси. Под действием появляющейся таким образом разности между температурой смеси и температурой среды возникают тепловые потери из реакционного объема в окружающую среду, которые
С ростом температуры смеси также увеличиваются. Следовательно, тепло, выделяющееся при химическом реагировании, расходуется на нагрев смеси и на тепловые потери.
Дальнейшее протекание процесса зависит от того, отводится ли все выделяющееся тепло в окружающую среду в виде тепловых потерь или же тепловыделение превышает тепловые потери. В первом случае наступает тепловое равновесие и устанавливается стационарная температура, несколько превышающая температуру окружающей среды. Во втором случае все большее повышение температуры приводит к самопроизвольному прогрессивному росту скорости реакции, бурному выделению тепла, т. е. к самовоспламенению горючей смеси.
На рис. 5-6 изображена зависимость тепловыделения <3Р и тепло - потерь фг от температуры. Скорость химической реакции с ростом температуры увеличивается прогрессивно согласно закону Аррениуса, поэтому тепловыделение в единице объема выражается экспоненциальной кривой
(1Р = 1г, е-Е1ЯТС»С>. (5-40)
В уравнении:
Кпё~Е1ЯТ — константа скорости реакции;
С — концентрация горючего газа;
П — порядок реакции;
<3 — теплота сгорания.
Теплоотдача, отнесенная к единице объема, является линейной функцией от температуры
С2, = «-£-(7’-7'.). (5-41)'
В уравнении:
А — коэффициент теплоотдачи;
Р и V — соответственно поверхность и объем сосуда, в котором находится горючая смесь;
Т — температура реагирующей смеси, принимаемая одинаковой во всем реакционном объеме;
То—температура стенок сосуда, равная температуре окружающей среды.
Стационарными режимами являются точки пересечения кривых <2Т и (2Г, в которых тепловыделение равняется теплопотерям. В зависимости от температуры возможны два стационарных режима: нижний 1 и верхний 2. До точки 1 тепловыделение больше теплопотерь, вследствие чего смесь будет разогреваться. Разогрев продлится до тех пор, пока температура смеси возрастет до Т1. При этой температуре ч? р = С2т - Дальше смесь не будет разогреваться, так как при температурах выше Т <3т><3р> и в случае, когда по какой-либо причине смесь перегреется выше Т1, она вновь охладится до той же температуры. В этом случае реакция приводит к разогреву смеси до температуры Ти которая несколько выше, чем температура сгенок сосуда Г0. Следовательно, нижний стационарный режим является устойчивым и характеризуется слабым разогревом, малой скоростью реакции, поэтому считают, что имеет место медленное окисление.
При разогреве смеси выше температуры, соответствующей точке 2, тепловыделение превышает теплолотери, в результате происходит прогрессивный разогрев, приводящий к самовоспламенению. При понижении температуры тепловыделение <3Р становится меньше теплопотерь (2т, поэтому система не может вернуться в начальное состояние, а переместится в точку 1. Таким образом, верхний режим неустойчив и практически не реализуем.
Будем теперь повышать температуру окружающей среды Г0, что графически изобразится переносом прямой С2т параллельно вправо. При некотором значении Гко кривые <3Р И (2т будут иметь одну общую точку К. Это состояние устойчиво по отношению к понижению температуры и неустойчиво к ее повышению. Точка К является критической: ниже соответствующей ей температуры Гк мы имеем стационарный режим, напротив, незначительное превышение температуры окружающей среды над Тко вызывает прогрессирующий саморазогрев смеси, проводящий к самовоспламенению.
Данный. метод исследования, в котором возможность наступления самовоспламенения рассматривается как достижение предельно возможного стационарного состояния, являющегося критическим, получил название стационарной тепловой теории самовоспла - м е н е н ия.
Поскольку при незначительном превышении То над критическим ее значением Гк0 и соответственно Т над Гк стационарное состояние невозможно и наступает прогрессирующий рос г температуры, в стацио-
Нарной тепловой теории за температуру самовоспламенения принимают Тк или более доступную измерению — 7^0- Разность температур ЛГ= = 7К—называется предвзрывным разогревом.
Следовательно, температура самовоспламенения зависит не только от природы и свойств горючей смеси, но и от условий протекания процесса, определяющих теплоотдачу реагирующей смеси, и поэтому не является физико-химической константой, а представляет собой результативную характеристику процесса.
Н. Н. Семенов [Л. 11] впервые математически определил температуру самовоспламенения из условия, что в точке касания кривой С? р с прямой (Это тепловыделение равняется теплопотерям и равны их первые производные по температуре, т. е.
|
|
|
|
Подставляя в уравнения (5-42) и (5-43) выражения (5-40) и (5-41) и после дифференцирования решая их совместно, получаем:
|
(5-44) |
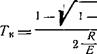
|
4ЯГко Е |
![]() Откуда
Откуда
(5-45)
Решение со знаком плюс перед радикалом отброшено, так как
Дает значение для температуры самовоспламенения порядка 10 000°С и
Выше, чего в действительности не может быть. Функция е при
Температуре Е/2Я имеет перегиб, и решение со знаком плюс отвечает пересечению прямой (Зт с кривой (Эр в области очень высоких температур.
Разлагая выражение для Тк в ряд и пренебрегая членами, содержащими (Гко)3 и выше, получаем:
|
Т __ тк I К (Тко)2 1 К ------ 1 0 | £-------- . Отсюда разогрев, предшествующий самовоспламенению,
|
Из уравнения (5-47) следует, что если разогрев АГ<ЛГК, то самовоспламенение невозможно, и, напротив, если АТ>АТК, то самовоспламенение может наступить.
Разогрев, предшествующий самовоспламенению, зависит от энергии активации и величины температуры 7*0, но, как правило, для реакций горения не превышает нескольких десятков градусов.
Таким образом, в стационарной тепловой теории определяется состояние смеси на пределе самовоспламенения, которое является возможным предельным стационарным состоянием. При незначительном превышении температуры смеси над Гк, отвечающей этому состоянию, что может произойти в результате повышения температуры окружающей среды над Т^о, или уменьшения интенсивности теплоотвода, стационарное состояние становится невозможным.
В критической точке интенсивность тепловыделения становится равной интенсивности теплоотвода (рис. 5-6, кривые С2Р и С2Т), а при дальнейшем повышении температуры Т0 свыше Гк0 превышает ее (рис. 5-6, кривые (Эр и (2ПТ). В последнем случае не все количество выделяющегося тепла может быть отведено в окружающую среду, а лишь некоторая часть его. Часть тепла, которая не может быть отведена, расходуется на нагрев смеси. Это способствует развитию химического реагирования и приводит за определенный промежуток времени, называемый периодом индукции, к самовоспламенению. Чем меньше доля тепла, идущего на нагрев смеси, тем больше период индукции. Так как в критическом состоянии выделяющееся тепло отводится полностью, то в стационарной теории температуре самовоспламенения отвечает большая величина периода индукции, а теоретически — бесконечная.
Стационарная теория имеет большое значение для выявления физико-химической сущности процесса самовоспламенения, но она не предназначена для расчетов форсированных топливосжигающих устройств с весьма малым периодом индукции.
В условиях сжигания топлив в камерных топках парогенераторов, в камерах сгорания газотурбинных установок (ГТУ) и в других форсированных устройствах период индукции ограничивается величиной порядка сотых долей секунды и поэтому в этих случаях следует пользоваться нестационарной теорией теплового самовоспламенения. При этом представляется возможность выявить динамику развития процесса самовоспламенения, а также влияние свойств топлива и физических условий на процесс самовоспламенения.

 Опубликовано в
Опубликовано в