Выделив задачу переноса энергии (тепла) благо­даря введению понятий коэффициентов теплоотдачи на поверх­ностях сопряжения тела и потока теплоносителя, а также при­няв распределение скоростей известным из отдельного рассмот­рения задачи гидродинамики течения, получим для канала теплообменного аппарата (как было показано в подразд. 1.2) систему уравнений (1.1) — (1-13) с краевыми условиями.

Структура каналов в теплообменных аппаратах такова, что течение теплоносителей можно оценить как одномерное, поэтому

Г" 51 ---------------------- Вычисление Z Г” 02 -------------- ТТЛ Вычисление У   Формула Формула   (5 11) (512)

€>.

_ С1

Вычисление 4 формула

Вычисление Prrat формула (5. Ю)

Вычисление £д t формула '5.9)

(5J)

Вычисление ibt формула (5.6)

Г - Et Вычисление Р формула. ‘ 0-46)

5ыра$сть Признак Нереальности Процесса

© Г - НЗ -±— Јдt - 1

I

(^Остаиоб ^

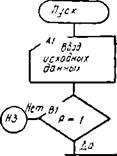
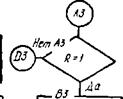
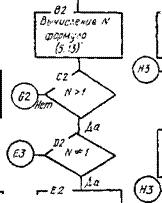
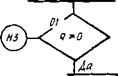
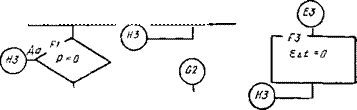
Рис. 5.8. Блок-схема ра с чета температурной поправки £д<

Представляется возможным строить два типа моделей решения задачи переноса тепла от одного теплоносителя к другому через твердую стенку.

Рассмотрим для простоты только взаимодействие одного теплоносителя с твердым телом (учет взаимодействия с другим теплоносителем не вносит методических изменений в структуру построения модели).

Следуя рекомендациям для ламинарного потока теплоноси­теля в приближениях теории пограничного слоя [104], уравне­ние переноса энергии (тепла) записываем в виде

Д2(,

(5.14)

5Л Ді. аТ + “^ =

СржРж ду

520 д2Ь ~2 + а7

Уравнение переноса энергии (тепла) для твердого тела

(5.15)

(Эи _ *т д1

СлтРт 'у Ох

Для потока теплоносителя рассматриваем область в пределах толщины пограничного слоя 0 < у < Л в канале длиной 0 < х < <1 при толщине стенки канала 5. Тогда для получения единствен­ного решения к уравнениям (5.14) — (5.15) присоединим краевые условия

= 0;

Л,

(5.16)

30 _ 50 _ а0   Дх Г=0 Дх Х='і ду У=—Ь

|т=л - /п; 0 |і=о = 0;

X — — ) — К«<1у -^Лу

Пели профиль скорости в канале неизвестен, а течение заве­домо турбулентное, вводят среднерасходную скорость Щ)с и осред - ненную температуру потока. Тогда для канала, симметрично омываемого внешним теплоносителем, система уравнении переноса энергии (тепла) в потоках и твердом теле примет вид (1.15):

Ді,

Дх 50

СотРт

СріРі + ^с! = — [0 (*> °» 1

Г^0 ^ дх~ ду2

Ди

А„г

Ді2 д12

СР2Р2^+^2^ = ~ІІ2 - ЦХ, 8, X)].

Присоединим к системе уравнений краевые условия Л|-=і'=Ло; ^2Іт=о = ^2о; 0|т=о = О(х, у, 0);

До

А,[в(х, 0, т) — Ґ! ] =ХТ

Ду

(5.17)

Г/=5

<*2 {її — 0 (а:, 3, ,)] = _ХТ^

Построив два типа моделей нестационарного переноса энер­гии (тепла) в системе теплоносители — твердое тело, необходи­мо выбрать метод и средства решения поставленных задач.

В задачах стационарного переноса энергии (тепла) основной целью расчета теплообменного аппарата является определение поверхности теплообмена, потерь давления в теплоносителях и конструктивное описание аппарата, а в задачах нестационарно­го переноса — определение изменения полей температур в по­токах теплоносителей и в твердом теле во времени.

Задачи, описываемые уравнениями в частных производных типа (5.14) — (5.15) и (1.14) — (1.16) с краевыми условиями, относятся к краевым задачам математической физики.

В справочнике по расчетам тепловых состояний [21] пред­ставлены материалы по применению различных методов и средств решения подобного рода задач.

Подготавливая объект, определяя цели, в качестве средства исследования следует выбрать структурные АВМ, сеточные АВМ (ЯС-сетки), цифровые ЭВМ.

В зависимости от выбранного машинного средства исследо­вания система уравнений и краевые условия аппроксимируют­ся системой обыкновенных дифференциальных уравнений либо системой алгебраических уравнений. Исследователь должен учитывать тип вычислительных средств, трудоемкость програм­мирования и подготовки задачи при требуемой точности полу­чения решения.

Чтобы показать возможности различных вычислительных средств, рассмотрим решение задач нестационарного переноса тепла, описываемое уравнениями (5.14) — (5.15), (1.14) — (1.16) с краевыми условиями.

Если в процессе исследования нас интересует детальное рас­пределение температур в потоке теплоносителя и в твердом теле по пространственным координатам, то система обыкновенных дифференциальных уравнений, аппроксимирующих уравнения (5.14) —(5.15), будет равна числу узловых точек в областях потока и твердого тела. В этом случае эффективно использо­вание аналоговой вычислительной машнны с сетками омических сопротивлений типа УСМ-1 [59], как показано в работе [10].

В задаче, описываемой уравнениями (5.14)—(5.15) и краевы­ми условиями (5.16), разобьем исследуемую область для потока теплоносителя и твердого тела сеткой прямых х = /Длг, у = )'Ау, где I, / = о, 1,2

Заменяя непрерывные функции ( (х, у, т) и 6 (*, у, т) сеточ­ными, аппроксимируем дифференциальные уравнения в частных производных обыкновенными для сеточных функций [21]. Для равношаговой сетки уравнение (5.14) примет вид

^ ~ и = % У‘-'+‘ “ (5■ 18>

—

Да,-

V

Уравнение (5.15) запишем так:

^2 (®‘+1 ■/ — 1 ®'—1, й Т~2 Ж — 26;. 1 + 0;, /—О

(5.19)

Уравнение (5.19) и краевые условия моделируются на обычной ^С-сетке для решения задач нестационарной теплопроводности [21, 38]. Уравнение (5.18) предлагается моделировать сеткой, состоящей из ЛС-элементов, дополненной усилителями с единич­ку

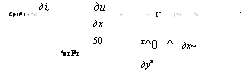
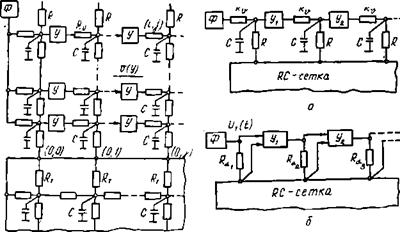
Рис. 5.9. Схема модели, описываемая уравнениями (5.23), (5.24) Рис. 5.10. Схема модели с усредненными параметрами потока

Ным коэффициентом усиления (рис. 5.9). Действительно, для узла с коэффициентами I, } на основании закона Кирхгофа можно записать ди^, 1 1

С ТГ + Т 1 ~ и‘• =' Т? — ил ^ +

(5.20)

+ (^(—1. / — /)•

Уравнение для электрической разветвленной цепи (5.20) будет аналогом уравнения (5.8), если выполнены условия

К1 а&у) _ п цж _ п Кшс ’ ду2 ~ %с’

Поскольку твердое тело также моделируется /?С-сеткой, для совместного решения необходимо выполнить условие

(5.21)

Яг ХЖД у,

/? _ *ТДу’

Напряжение и| на выходе из формирователя Ф является ана­логом температуры набегающего потока. Конвективный перенос в движущемся потоке будет существенней, чем кондуктивнын,
поэтому для исключения возможности обратных токов целесооб­разно в направлении течения включить операционные усилители с коэффициентом усиления, равным единице.

Таким образом, АВМ с /?С-сстками позволяют решать со­пряженную задачу переноса тепла в твердом теле и ламинар­ном потоке, если задан профиль скоростей в пограничном слое.

Решение задачи, описываемой системой уравнений (1.14).— (1.16) с. краевыми условиями (5.17), можно осуществить на АВМ с RC-сетками, как это показано в работе [10]. В этом случае уравнения энергии потоков моделируются /?С-цепочка - мн, дополненными усилителями с единичным коэффициентом усиления (рис. 5.10). Расчет параметров ^С-цепочек осущест­вляется так же, как и в предыдущей задаче.

Если в рекуперативном теплообменном аппарате при иссле­довании нестационарных процессов переноса энергии прене­бречь теплоемкостью стенок, разделяющих потоки, то матема­тическую модель аппарата можно представить уравнениями

(1.20) — (1.21) с начальными условиями (1.22) — (1.23). По­кажем, что для решения задач такого типа наиболее эффектив­но использование структурных АВМ.

Пусть температура теплоносителя, обтекающего трубный пу­чок, постоянна. Подобные условия возникают при обтекании трубного пучка влажным конденсирующимся паром. Тогда за­дача переноса тепла во втором теплоносителе описывается урав­нением энергии

(5.22)

Разобьем всю длину канала сеткой с шагом h, тогда урав­нение (5.22) аппроксимируется системой обыкновенных диф­ференциальных уравнений по временной координате.

В инженерной практике наиболее широко используются структурные АВМ типа МН-7, имеющие шесть интеграторов. Для решения уравнения (5.22) на МН-7 целесообразно шаг сет­ки hi выбрать так, чтобы в области исследования насчитыва­лось шеСть узловых точек. Тогда система обыкновенных диф­ференциальных уравнений, аппроксимирующих (5.22), примет РИД

(III _

= — а.Т 1 - f - а.То + а{Гн — а{Гi; - jr = — -+- o.{Ti - j - а{Г,, — а<{Г2

(5.23)

——fliT’4 - J - aTi + О-гТн — О2Т3',

Л

— - = — CI1T5 й[Тз - f «2ТN — CI2T

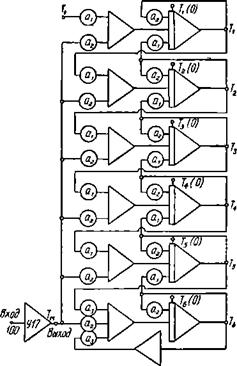
Рис. 5.11. Блок-схема решения задачи переноса тепла в потоке на АВМ

ЛТс

-гг = — аТъ +а{Т4 + а2Ти—а2Т5;

В - Ь 0-зТз -|- а{Гп — сцТ§,

Здесь а = шс/2/гь а2 = kZ/pcpSi ал = wjh. В случае неравно - шаговой сетки коэффициенты Я| во всех уравнениях бу1$т раз­личны.

В соответствии со структурной схемой (рис. 5.П) системы уравнений (5.23) для моделирования на МН-7 оказываются за­действованы все интеграторы, шесть сумматоров, один инвер­тор. и вспомогательный операционный усилитель У-17. Задача рассматриваемого объема использует все вычислительные поз - можностн машины МН-7.

При необходимости решения задачи аппроксимируемых до­статочно большим числом обыкновенных дифференциальных уравнений целесообразно применение более мощных АВМ.

Важнейшие достоинства структурных АВМ при изучении процессов нестационарного переноса — визуализация протека - мия процессов и возможность оперативного воздействия на оп­ределяющие процесс факторы [И, 50].

Благодаря стандартным программам решения систем обык­новенных дифференциальных уравнении на современных ЭВМ, использование их для решения подобных задач не представля­ет проблем. Ограничения могут диктоваться лишь предельно до­пустимым порядком системы, реализуемой в стандартной про­грамме.

Наиболее эффективно применение ЭВМ в случае реализа­ции прогоночных методов [73] для анализа аппаратов с простой геометрией каналов. При сложной геометрии проблема разра­ботки и отладки программы оказывается определяющей, тогда аффективны методы, ориентированные на АВМ с /?С-сетками,

Применение структурных АВМ целесообразно в задачах ана­лиза, когда необходима прежде всего качественная оценка ха­рактера переходных процессов и влияния на них входных и воз­мущающих воздействии.