Математическая модель должна с достато­чной точностью описывать определенные свойства объекта ис­следования. В настоящее время используются следующие ме­тоды получения математических моделей: теоретико-аналитиче­ский, экспериментально-статистический, статистического моде­лирования (Монте-Карло).

Применение того или иного метода зависит от особенностей теплотехнической системы, ее сложности, а также от стадии исследования или разработки — технические предложения, эс­кизный, технический и рабочий проекты, изготовление, действу­ющий объект.

Теоретико-аналитические методы составления математиче­ской модели в задачах оптимизации получили наиболее широкое распространение. Они пригодны для всех стадий разработок и единственно возможны при исследовании новой техники на ста­дии проектирования, ибо установки еще нет и «испытывать» можно только модель. Кроме того, аналитические методы дают возможность относительно легко выявить влияние отдельных факторов, выделить среди них наиболее существенные и опре­делить возможности целесообразного упрощения расчетов. Для исследования действующих объектов и в некоторых других случаях, когда сложность явлений или неполное знание их су­щественно затрудняют получение математических моделей ана­литическим методом, используют экспериментально-статистиче­ский метод и метод Монте-Карло.

В решении проблемы оптимизации технической системы можно выделить задачи нескольких классов (по иерархии уров­ней решения). В основу такой классификации может быть положена аналогия расчленения существующих теплотехниче­ских систем на составляющие элементы подсистемы: теплотех­ническая система—-энергетические и другие установки — от­дельные агрегаты и аппараты — их отдельные звенья, детали (табл. 16.1).

Высшим, а следовательно, и наиболее сложным уровнем является обеспечение оптимального решения в целом по тепло­технической системе. Следующий уровень — это отдельные уста­новки, математические модели которых могут быть не менее сложными; далее идут отдельные агрегаты и аппараты, по кото­рым к настоящему времени накоплено достаточное количество частных решений; это же относится и к отдельным деталям.

В зависимости от стадии исследования или разработки мате­матическая модель может отличаться также и степенью детали­зации, большим или меньшим количеством допущений. Необхо­димо также иметь в виду следующее: если для определения функции цели использовать, например, современные методы

16.1. Классификация математических моделей при оптимизации теплотехнических систем

Уровень	Объект оптимизации	Примеры
Высший	Теплотехническая система	Оптимизация структуры тепло­вой части ТЭЦ, АЭС и т. п.
Сложный	Энергетические и другие тепло­вые установки	Паросиловая установка, газо­турбинная установка
Усложнен­ Ный	Некоторые комплексы аппара­тов, отдельные агрегаты	Конденсатор-градирня, газовая турбина — регенератор, тепло - обмениые, массообменные аппа­раты
Сравнитель­но простой	Отдельные детали	Выбор оребрения трубок в теп­лообменнике

Расчета теплообменных аппаратов, связанные с решением сис­тем нелинейных дифференциальных уравнений, и в то же время приближенно оценивать их стоимость, не смотря на громоздкость и сложность алгоритма, требуемое повышение точности конеч­ных результатов не достигается. Поэтому на ранних стадиях проектирования выбирают обычно приближенные методы тепло­вого и гидромеханического расчета оборудования и оптимизи­руют, как правило, те параметры, которые наиболее резко вли­яют на экономические и массогабаритные показатели теплотех­нической системы.

Таким образом, при оптимизации теплотехнической системы четко прослеживаются два подхода: сложную систему рассмат­ривают как единое целое или сводят ее к взаимосвязанным задачам оптимизации отдельных частей (декомпозиционный ме­тод). Применение того или иного подхода обусловлено целью и задачами исследования, однако в большинстве случаев первый подход более перспективен.

В пользу первого подхода говорит, например, следующий факт [22]: расчеты таких оптимальных параметров, как темпе­ратура охлаждающей воды и кратность охлаждения, проведен­ные отдельно для конденсаторов и систем охлаждения, дают противоречивые результаты. Увеличение кратности охлаждения и уменьшение температуры воды, с одной стороны, снижают стоимость конденсатора, но, с другой — приводят к возрастанию стоимости системы охлаждения (градирни, водохранилища, брызгальные бассейны).

Поэтому правильный выбор параметров оптимизации возмо­жен лишь при рассмотрении комплекса конденсатор — система охлаждения, для которого наблюдается ярко выраженный ми­нимум суммарной стоимости. Это относится также к теплотех­ническим системам турбина — конденсатор, газовая турбина — регенератор и т. п.

Оптимизация теплообменных аппаратов как самостоятельная задача применяется в большинстве случаев для минимизации массы аппарата или его объема, а также как одно из звеньев декомпозиционного метода. В большинстве случаев работа теп­лообменника в технологической цепи с другими устройствами существенно влияет на конечные результаты всей работы систе­мы. Тогда также более обоснован первый подход, который мы рассмотрим более детально на примере работы утилизационной силовой установки на низкокипящих рабочих телах.

Важным этапом составления математической модели явля­ется выбор независимых переменных (факторов) и интервалов варьирования, а также их нулевого уровня. Независимые пере­менные имеют область определения, которая может быть непре­рывной и дискретной. При проектировании в качестве незави­симых переменных принимают технологические и конструктив­ные параметры, при оптимизации действующих теплотехнических систем — только технологические параметры, обеспечивающие наилучшие результаты функционирования объекта.

В качестве нулевой точки для каждой переменной принима­ется такое значение, которое соответствует наилучшему извест­ному значению параметра оптимизации.

При выборе интервалов варьирования независимых перемен­ных необходимо иметь в виду, что по мере уменьшения интер­вала увеличивается точность определения оптимума, но требуется большое количество вычислений. Естественно, что увеличение интервалов варьирования действует противоположно, и поэтому эти величины выбирают, исходя из компромисса между двумя этими требованиями.

Оптимизация параметров и характеристик оборудования теплотехнических систем очень часто сопряжена со многими техническими ограничениями. Они касаются самих независимых переменных или промежуточных величин, влияющих на выбор исследуемых параметров. В первом случае ограничения учиты­ваются в явном виде, во втором — необходимо вводить допол­нительные условия, обеспечивающие их соблюдение.

Математическую модель теплотехнической системы состав­ляют из нескольких автономных частей: блока расчета элемен­тов объекта и процессов, протекающих в них; блока экономи­ческого описания системы и ее функционирования; блоков поиска оптимальных параметров с функциями ограничений.

Большинство задач оптимизации теплотехниче­ских систем сводится к методам нелинейного программирования. Рассматривая «прямые» методы (или методы спуска), мы харак­теризуем их типом вычислений на каждой итерации (каждый метод спуска является итерационной процедурой) и стратегией поиска.

По типу вычислений методы спуска подразделяются на ме­тоды, требующие вычисления только функции цели, расчета помимо этого первых производных, вычисления первых и вторых производных.

Методы оптимизации, не использующие производные, обычно называют методами поиска, в которых направления минимиза­ции полностью определяются на основании последовательных вычислений целевой функции.

По стратегии поиска к первому типу относятся методы Гаус­са — Зейделя, Хука и Джизса, «золотой поиск» и др. [99]. К ме­тодам второго типа можно отнести методы наискорейшего спуска, градиентные и другие. Третий тип требует аппроксимации функции цели в окрестности рабочей точки и исследования ха­рактера ее поверхности.

Проблема выбора метода поиска оптимума пока еще не формализована и поэтому является творческой задачей. При выборе метода оптимизации наряду с общим объемом вычисле­ний необходимо учитывать устойчивость метода к погрешностям, область сходимости, требуемый объем памяти и удобство ре­ализации на ЭВМ и т. д.

При вычислении производных в рассматриваемых нами слу­чаях оптимизации теплоэнергетического оборудования встреча­ются серьезные трудности. В задачах с достаточно большим числом переменных довольно трудно или даже невозможно получить производные в виде аналитических функций, необхо­димых для градиентного алгоритма или алгоритма, использу­ющего производные второго порядка. Хотя вычисление аналити­ческих производных можно заменить вычислением производных с помощью разностных схем, возникающая при этом ошибка, особенно в окрестности экстремума, может ограничит-ь приме­нение подобной аппроксимации. Поэтому более приемлемы ме­тоды минимизации, не требующие вычисления производных и основанные лишь на вычислении значений функций в каких - либо специально подбираемых точках.

Рассмотрим некоторые, наиболее часто применяемые методы оптимизации функции

У=}{ХХ, Х 2, ..,*„). (16.1)

Метод Гаусса — Зейделя. Алгоритм этого метода прост и заключается в последовательном изменении поочередно каждого

Фактора до тех пор, пока функция цели не примет экстремаль­ное значение. Алгоритм метода следующий:

1. Выбираем исходную точку уа= (я10, х20, хп0) и шаг варьирования Axt (i=l, 2, ..., п) по каждой переменной.

2. Определяем значение критерия оптимизации в точках

Уi, i = f(*i + A*i, х2, х3, ..., хп) yil2 = f(xt — Axlt х2, х3, х„)

3. Сравниваем полученные значения функций Ум, У,2 и вы­бираем направление движения экстремуму.

4. Осуществляем движение вдоль оси х в направлении экст­ремума y,k — f(xx+kAxu х2, ..., хп) (k=l, 2, 3 ...) до тех пор, пока не будет достигнут частный экстремум по переменной хи который определяется в случае минимизации функции у 1,ь+|> >У.к. Достигнутая точка является исходной для осуществления движения в направлении оси х2 и т. д. После я-го движения переходим К (л+1)*му движению ВДОЛЬ ОСИ XI, затем к (п + 2)- му движению ВДОЛЬ оси х2 и т. д.

Поиск прекращается в точке, любое движение из которой приводит к увеличению (при поиске минимального значения) критерия оптимизации.

В практических задачах вычисление значений функций мо­жет оказаться весьма трудоемким, и здесь большую ценность приобретают методы, позволяющие решить задачу минимизации с требуемой точностью на основе вычислений значений функции в возможно меньшем количестве точек. Простым и удобным для использования на ЭВМ является выбор отрезка локализа­ции точки минимума и нахождение минимального значения функции на этом отрезке методом «золотого сечения».

Рассмотрим алгоритм этого метода. Пусть отрезок (а0, Ь0) содержит оптимальную точку. Необходимо уменьшить его длину до наперед заданной величины е. Заданы дроби Фибоначчи F| = = (3— Г5)/2^ 0,382, F, = (К5- 1)/2=ь 0,618.

Пусть а0 = а/, Ь0 = Ь/. Если а/, 6/ известны, значения а/+1 и bj+] находим следующим образом.

1. Определяем величины lj = aj + F]{bt — а,) или li = b/ — — F2(bi — aj) ri = a, + F2(bi — а,).

2. Вычисляем значения функции у в точках Z, и г, и исполь­зуем соотношения

«/+,=//, b,+i = bh если у(1,)>у(г,);

Al+l~ajt ц/+, = Г/, если у{Ц) <£/(/-/).

3. Поиск прекращается, когда (ц/+! — a/+i)<е, а искомому параметру х{ приписывается значение лс,-= (a/+1 + ц,+1)/2.

Метод формального поиска. Этот метод предназначен для нахождения оптимального значения функции (16.1). Необходи­мо иметь в виду, что метод Гаусса — Зейделя работает плохо, если имеется взаимодействие между переменными. Для этих случаев более подходящи методы формального поиска, Хука

И Дживса [99]. На область изменения независимых переменных хх, Х2, ..., хп могут быть наложены ограничения вида

Рс=(х1,х2, ..,*„)< 0 (/ = 1,2,3, ., т) (16.5)

Алгоритм метода следующий:

1. Выбираем произвольную точку внутри области изменения переменных хи х2, ..., хп, удовлетворяющую условиям (16.5).

2. Изменяя отдельно каждую независимую переменную на заданное приращение Дх;, фиксируем точки, в которых проис­ходит убывание (если ищем минимум) функции/(хь х2, ..., хп). Точки, в которых обнаружено убывание функции /, определяют направление ее убывания.

3. Делаем последовательные шаги в этом направлении до тех пор, пока происходит убывание функции

4. Если после некоторого числа шагов функция / не убывает, то, производя снова пробные движения, определяем новое на­правление убывания функции и т. д.

5. Если пробные движения не приводят к убыванию функ­ции /, уменьшаем шаг пробных движений Ду и повторяем пробы.

6. Если шаг пробных движений окажется меньше заданного, процесс поиска экстремума заканчиваем.

Симплексный метод оптимизации. Благодаря простоте и вы­сокой эффективности метода, особенно при большом количе­стве переменных, он широко применяется в различных отраслях науки и техники.

Симплексом называют простейший выпуклый многогранник, вершины которого равноудалены от центра фигуры (например, симплекс на плоскости имеет вид равностороннего треугольни­ка, в трехмерном пространстве — тетраэдра).

Основная идея этого метода заключается в том, что по из­вестным значениям целевой функции в вершинах симплекса находится направление, в котором требуется сделать следующий шаг, чтобы получить наибольшее уменьшение (увеличение) кри­терия оптимальности.

При оптимизации используется основное свойство симплекса: в нем можно условно отбросить одну вершину и найти новую, симметричную отброшенной, получив таким образом новый симплекс. Повторяя такую процедуру, можно осуществить пере­мещение симплекса в факторном пространстве.

Доказано, что если каждый раз отбрасывать ту вершину, значение выходного параметра в которой будет худшим по срав­нению с другим, центр симплекса перемещается к оптимальному значению.

Алгоритм метода следующий:

1. Выбираем исходные значения переменных дсю, Хго,

•которые принимаются за центр симплекса.

2. Выбираем интервал варьирования по каждой переменной Дх, Ах2, ..., ДХк-

3. Значения координат вершин симплекса г; определяем с по­мощью табл. 16.2, в которой г і, Яі — радиусы вписанных в сим­плекс и описанных вокруг него гиперсфер:

Ті = 1 ; Пі = і/ * (г = 1,2,. ., к).

У 2І (і + 1) V 2(£+1)

16.2. Таблица координат симплекса № П/п 21 22 2з Г4 Ч-1 Ч 1 '1 (0-5) Г2 (0,289) Г3 (0.204) Л4 (0.158) Гк-1 Гк 2 -Я, (0,5) Г2 (0,289) 'з (0-204) #4 (0.158) Гк-1 Гк 3 0 -Я2 (0,589) Г3 (0.204) Ч (0.158) Гк-1 Гк 4 0 0 -Я3 (0,621) /4 (0.158) Гк- Гк 5 0 0 0 -Я4(0.632) Гк-1 Гк /V —2 0 0 0 0 Гк- Гк N — 1 0 0 0 0 Гк N 0 0 0 0 0 -«*

Примечание. В скобках представлены значения гс, Я,- в кодирован­ном масштабе.

На основании приведенных таблиц составляется план вычис­лений в исходном положении симплекса. Значения переменных хс в натуральном масштабе определяются по формулам = л^о + + 2,-Дд:((1 = 1, 2, А), где л:,- — значение i-й независимой пере­

Менной в вершинах симплекса.

4. Вычисляем значения у в найденных расчетом вершинах и от­ражаем вершину, в которой это значение наибольшее (при мини­мизации функции цели). Координата новой вершины симплекса

/ 1 П * Iя

Определяется ПО формуле л£+1 = 2 ( 2 Хш — X*, где — Хш—

и— 1 ) и=1

Среднее арифметическое из координат хс вершин за исключением «худшей»; XI — координата «худшей» вершины.

В результате применения рассмотренной процедуры исклю­чения вершин симплексов с. наибольшим значением целевой функции процесс сводится к минимальному значению функции у.

5. Поиск прекращаем, если длительное перемещение симп­лекса не приводит к улучшению параметра у или если разница в значениях параметра оптимизации «худшей» и «лучшей» из вершин симплекса находится в пределах погрешности измере­ния у.

Рассмотренный метод—один из наиболее простых методов оптимизации теоретических и экспериментальных моделей теп­лотехнических систем. Среди модификаций симплекс-метода для аналитической оптимизации наиболее подходит модификация с автоматическим выбором шага. Блок-схема этого метода при­ведена в книге Д. Химмельблау [99].

Рис. 16.1. Схема и цикл фреоновой установки с регенерацией тепла

Перечисленные методы позволяют находить локальный ми­нимум целевой функции. На практике совпадение локального и глобального минимальных значений целевой функции может быть проверено с помощью нескольких начальных векторов не­зависимых переменных.

Пример. Оптимизация силовой утилизационной установки. В нашей стране и за рубежом работает ряд установок, использующих в качестве рабочих тел фреоны и другие низкокипящие вещества. Для иллюстрации выбрана утилиза­ционная установка, работающая на фреоне-С318 и использующая отходящие газы технологических агрегатов в качестве Греющего теплоносителя. Исполь­зование таких установок для утилизации низкопотенциального тепла перспек­тивно.

Фреоновые установки работают в двухконтурно Я схеме (рис. 16.1). Тепло отходящих газов технологических агрегатов через стенку теплообменника - парогенератора I передается фреону, а охлажденные отходящие газы с помощью дымососа выбрасываются в трубу (процесс а—о). Во втором контуре фреон нагрезается до температуры /г (процесс б—1) и расширяется в турбогенера­торе II (процесс 1—2). Отработавший в турбине пар охлаждается в тепло­обменнике-регенераторе III (процесс 2—3), а затем конденсируется в конденсаторе IV (процесс 3—4) при давлении рк. Конденсат питательным насосом V подается через теплообменник-регенератор в парогенератор (процесс 4—5—6). Для подачи охлаждающей воды в конденсатор служит циркуляционный насос VI. Вода в конденсаторе нагревается на температуру Д<4 (процесс с— (1).

Исходные данные: количество отходящих газов Ор = 69,5 кг/с; средняя

Температура откодяїцих газов <г = 290 °С; температура охлаждающей воды (р -- 20 °С; годовое количество часов работы установки т = 7500 ч/год.

Ставится задача за счет оптимизации параметров утилизационной силовой установки получить максимально возможный народнохозяйственный эффект.

В примере рассматривается этап оптимизации, который мож­но условно отнести к стадии разработки эскизного проекта. На этом этапе определяются, как правило, параметры теплообмен­ных аппаратов, нагнетателей и энергетического оборудования, связанные с характеристиками термодинамического цикла, а также расходы и скорости теплоносителей, которые должны обеспечиїь возможно больший эффект (3-гпіп) силовой уста­новки.

В нашем примере оптимизируются следующие независимые па­раметры л'іі значення температуры хі=/і, температурные пере­пады Хч = Д^і, х3 = Д/г, *+ = Д/3, Ху = Д^ (см. рис. 16.1), а также скорости теплоносителей Л:е=Шц, *7=1012, *8 = “>21, *9 = ^22, *ю = *=а»з1. Для скоростей теплоносителей приняты такие обозначе­ния: доп — отходящие газы в парогенераторе; гг» і г— фреон в па­рогенераторе; щ|21 — парообразный фреон в регенераторе; и»22 — жидкий фреон в регенераторе; ш3і — скорость охлаждающей воды в конденсаторе. В рассматриваемом примере верхнее дав­ление не оптимизируется. Оно выбрано из предварительного' анализа равным 5 МПа. Конструктивно-компоновочные харак­теристики элементов, тип поверхностей теплообменников, тур­бин и другого оборудования предполагаются заданными. Варь­ирование типом конструкций элементов установки увеличивает объем хранимой в памяти машины информации и значительно усложняет алгоритм решения. Данная задача проще решается последовательным автономным расчетом поиска оптимального значения для каждой из перебираемых конструкций, что позво­лит конструктору остановиться на наиболее рациональном из •всех возможных проектных вариантов.

Введены упрощающие предпосылки: брались постоянными материал, диаметры, шаги и характеристика оребрения трубок в парогенераторе, регенераторе и конденсаторе, а их компоновка осуществлялась в теплообменниках квадратного сечения. В ре­зультате оказалось возможным, не снизив точности, существен­но упростить решение задачи,-

В примере рассмотрен один конструктивный вариант — для всех элементов установки выбраны кожухотрубчатые аппараты. Парогенератор и регенератор выполнены соответственно из стальных и латунных труб с накатанными ребрами (внутренний диаметр 14,5 мм, коэффициент оребрения 2,3), а конденсатор — из латунных трубок диаметром 17/19 мм. Турбина радиально­осевого типа отличается простотой конструкции и низкой стои­мостью изготовления.

Предварительно проводится математизация физических свя­зей в установке в виде аппроксимирующих зависимостей. Для фреона-С318 получены следующие аппроксимирующие зависимо­сти в диапазоне параметров, в котором возможна работа утили­зационной установки:

Р = 0,5 МПа; I, = 0,003457/? — 0,241/, + 673,9; (16.6)

Р = 0,5 МПа; 5, = 7,492 10~— 6,511 Ю“4/] + 1,5304;

(16.7)

/2 = 100,875* + 86,03«, —307,98 + (/* — 30) 1,65; (16.8)

/ > 100° С, 12 = 603,8 + 0,925/2 (16.9): Цл = 498,68 + 1,128/*;

(16.10)

Рк = 0,001488/1 + 0,02225/^ + 1,647 (16.11) (к = —0,568р + + 12,831/7* — 9,364. (16.12)

С учетом всех факторов строится математическая модель

Проектирования утилизационной установки. В качестве принци­пиальной схемы счета принят прямой расчет полезной мощности установки, площадей теплопередающих поверхностей теплооб­менников и гидромеханических потерь при некотором наборе независимых переменных. Для этих же независимых переменных определяется и показатель оптимальности.

Рассмотрим подробнее эти блоки математической модели. Главными составными элементами теплотехнической системы в общем случае служат различного рода теплообменная, и мас­сообменная аппаратура, нагнетатели (насосы, вентиляторы, ды­мососы, компрессоры и т. п.), силовые установки.

Построение математической модели начинают с составления формализованного описания процессов, протекающих в тепло­технической системе. На основе уравнений теплопередачи и гид­ромеханики определяют активную поверхность теплообмена и мощность нагнетателей А^, а из термодинамического анализа циклов — теоретическую мощность турбины Л'т. Имеют место очевидные формулы:

^ = СЫ{ШЬ (16.13)

N1 = С, Др,/(р£тг() (16.14) Мг = вт (г, —;2). (16.15)

Здесь фг—тепловая нагрузка на теплообменный аппарат; £,•— коэффициент теплопередачи; Д/(- — температурный напор; 6£) 6Т— расход рабочих сред; Дрс — гидравлические потери; р£— плотности теплоносителей; гц — к. п. д. нагнетателей; (^ — г2) — теоретический теплоперепад на турбине.

Переход от активной поверхности теплообмена к массе для кожухотрубчатых аппаратов представим в виде

Где Ш( — масса единицы теплопередающей поверхности; с*— с, ношение массы труб к массе аппарата. 0 т’

После подстановки в формулы (16.13) — (16.15) знач^ соответствующих коэффициентов теплоотдачи и гидравличе^иик сопротивлений они могут быть развернуты через технолог*ких ские и конструктивные параметры. Например, для теплооб>иче" ной аппаратуры получены зависимости в следующем виде: ,1ен"

Для гладких труб

Мі = -

І І А<і

____ ї_____ +_______ !_____ „її, 'М7)

К+ *(*!<)»"< (сі +

...т!> Д/і

(сі + 2() ш£

•Я,

Іаі + V'») <

Для ребристых труб Мі =

Оі

•(1^.13)

Здесь Пі — термическое сопротивление, учитывающее загрязне»

4>і — коэффициент увеличения поверхности. Коэффициенты те»1ия: отдачи (аі +Ьііи)яии, (с; + ^20а'й в формулах (16.17) — (16 "

Определяют из критериальных зависимостей для области разви турбулентного движения рабочих сред, так как только в зого условиях можно спроектировать установку с приемлемыми техТих логическими показателями. н0'

Мощности нагнетателей разворачиваем с учетом

І, В/Ш2,

+ ^вх + Нвых + (16Ч9)

Рі = сц + Ьі іі, (16^20^

Где X,-, ?вх, 5ВЫХ, Ём— коэффициенты сопротивления трения, ме ных сопротивлений входа, выхода и поворотов; г( — число хо ст" в теплообменнике; — отношение длины труб к диаметру. ^ов Плотность теплоносителя в сечении, где находится мест)

Сопротивление, принята по средней температуре теплоносит^ое в аппарате. Погрешность от такой замены невелика, а алгор^!Л5| расчета значительно упрощается. Поверхность теплообмена к/м денсатора ^н'

Рк=0к ІЯ - (16.^^

Удельный теплосъем конденсатора ц определяется решенц трех уравнений: ем

(16*^2)

Д/ — 6п ~Ь бохл»

Ц = ап9п = сопэ1 вп’75; (16.

Здесь 0П, йохл — температурные перепады между конденсирующимся

U 5сп

Фреоном и стенкой, между стенкой охлаждающей водой; j—,

Каг

^------- термическое сопротивление стенки отложении; оп, аохл —

Азаг

Коэффициенты теплоотдачи со стороны паря и охлаждающей воды.

(16.25)

Для определения коэффициента теплоотдачи при пленочной конденсации сухого насыщенного пара на горизонтальных тру­бах можно использовать формулу Д. А. Лабунцова [45]:

1/3 i rpv

Re = 3,25Z0'25,

Где Re = a&tr. R — число Рейнольдса; Z = htnR

•число Григуля; X, V — коэффициент теплопроводности и вязкости при температуре насыщения; г, р— теплота парообразования и плотность конденсата.

В случае выбора в качестве функции цели экономических критериев необходимо ввести в математическую модель блок экономического описания системы. Установление функциональ­ной связи между технологическими, конструктивными характе­ристиками теплотехнической системы и экономическими пока­зателями дает возможность наиболее обоснованно выбрать наи- .лучший вариант.

Применительно к особенно распространенным элементам такой системы, а именно теплообменным аппаратам и нагрева­телям, рассмотрим более подробно современные методы и струк­туры расчетов экономических критериев как одного из блоков математической модели.

Капиталовложения К включают те затраты, которые влияют на выбор оптимального варианта:

K

П

Т

К — Кт -t - Km. i + Кн, 4“ К„,н + Ккип + КСр£ (16.26)

Здесь Кт, Кв, —капитальные вложения в теплообменный аппа­рат и нагнетатели, включающие транспортные расходы; Км. т, К. н,- —стоимость монтажа теплообменника, нагнетательного устройства; Ккип — капиталовложения в КИП и автоматику; Корг- —затраты на приобретение рабочих сред для первоначаль­ного заполнения системы.

Для реализации алгоритма оптимизации на ЭВМ цена теп­лообменных аппаратов может быть определена из соответству­ющих прейскурантов:

К1=М, Цм, или Кт= FilXr,

■где Цм, Цр - — цена аппарата, руб./т, руб./м2.

Для определения значений Ци, Ц/г необходимо проводить ап­проксимацию табличных данных ценников.

Капитальные вложения в нагнетатель

К Яi = NlкИi. (16.28)

Здесь N1 — мощность, затрачиваемая нагнетателем на преодоление гидравлического сопротивления теплообменника соответствующим теплоносителем; кн£—капитальные вложения, приходящиеся на единицу установочной мощности нагнетателя, включая силовое оборудование и вспомогательные конструктивные элементы.

Используя метод коэффициентов и выбирая любой подходя­щий нагнетатель (эталонный), для которого известны кн. э и Ыэ, получаем

1-п

Кн, = кн. з ~N~j • (16.29)

Где к„.э — удельные капиталовложения в эталонный нагнетатель; Nз — мощность эталонного нагнетателя; п = 0,5 ч - 0,9 (для хими­ческих и нефтехимических производств п 0,75).

Стоимость монтажа теплообменных аппаратов зависит от мас­сы аппарата Ма и места монтажа [4,28]:

М„ (ЛГ + пз

М* <6’ <16-30> 6 < М„ < 20, Км. т = о,1715Ма —0,54 ’ (16.31)

Ма>20, Км. т = Ма (29,26 — 0,325Ма); (16.32)

Р = 1 при монтаже на открытой площадке.

Эксплуатационные расходы Э включают в себя основные расходы, непосредственно влияющие на выбор варианта. Они могут быть разделены на две группы: пропорциональные капи­таловложениям и не зависящие от капиталовложений.

К первой группе относят амортизационные отчисления на капиталовложения, расходы на текущий ремонт и содержание оборудования; ко второй — расходы энергии на привод нагне­тателей, пропорциональные их мощности, расходы на восполне­ние рабочих сред, основную и дополнительную заработную плату персонала Зп, обслуживающего оборудование, и некото­рые другие производственные расходы Зпр.

Для определения эксплуатационных расходов можно исполь­зовать зависимость

Т т к

Э = Эт-а -4- Эн, -)- ^ Ээ -Ь 5] -|- Зп -4- 3„р, (16.33)

1^1 ,-=1 1=1

Где Эт а, ЭН1.— амортизационные отчисления, отчисления, на ремон и содержание теплообменника и нагнетателя; Э3£ — стоимость энергии, необходимой для привода нагнетателя; 3Т(. — стоимость восполнения і-го теплоносителя.

При оптимизационных расчетах удобно представить

Эу. а = Кг. а (<2т. а Ч- Рт. а) (16.34); Зні = Кні (#н "І- Рн)і (16.35) Э3i = NнДэxP (16.36); Зт. = ОпЦТ1.тг 10-3. (16.37)

Здесь Ст. а. Рт. а» <2„, рн — ГОДОВЫе НОрМЫ амортизации И раСХОДОВ на текущий ремонт теплообменников и нагнетателей; Цэ — цена электроэнергии, руб./(кВт ч); тг — время работы оборудования в году, ч/год; <0Т1 — расход г-го теплоносителя, кг/ч; ЦТ£ — цена і-го теплоносителя, руб./т.

Прочие экономические факторы и коэффициенты. Амортиза­ционные отчисления 5а определяются по установленным нормам амортизации. Этн нормы для различных элементов основных фондов неодинаковы. Процент амортизационных отчислений на производственное оборудование зависит от условий эксплуата­ции и составляет 7,5—8 % [67].

Затраты на текущий ремонт оборудования 5тр (в процен­тах— р) могут приниматься в размере (0,1 ^-0,2) 5а [67].

Продолжительность работы оборудования тг в течение года зависит от многих факторов и принимается при учете условий работы каждого производства. В среднем тг = 7000 ч/год.

В блок экономического описания установки введены следу­ющие стоимостные показатели оборудования теплоносителей;

Парогенератор С„ = 625 руб./т; регенератор Ср = 1380 руб./т конденсатор Ск = 1355 руб./т; турбогенератор Ст = 1500 руб.; питательный насос Сп. н = 285/У°;,5 руб.; циркуляционный насос Сц.„ = 58,5Д^и:,45 руб.; дымосос Сд=28//д'4 руб.; фреон-С318 Сф = 6 руб./кг; охлаждающая вода С0 = 1,1 коп./м3. Стоимость замещаемой электроэнергии Цэ=15 руб./ (1000 кВт-ч).

С помощью зависимостей (16.6) — (16.37), а также формулы (16.38) разработан алгоритм и программа для ЭВМ и выпол­нено расчетное исследование для определения полезной мощно­сти турбогенератора

Мп = Мт'ЯоГЦтЦг — ДЛ^т — ДОп. п — — А/д. (16.33)

Здесь - цоі, ут, т]г — относительный внутренний, механический к. п. д. турбины, к. п. д. электрогенератора; ДМТ — потери мощности тур­бины вследствие изменения противодавления из-за гидравличе­ских сопротивлений; ІУП.„, А^ц. н, Мд — мощности питательного, цир­куляционного и тягодутьевого устройства.

Значительный объем результатов расчетного исследования заслуживает самостоятельного обсуждения. Ниже приведены лишь некоторые данные, иллюстрирующие возможности рас­смотренного алгоритма.

Оптимизируемые величины

5,0 0.377 80,3 12.1 8,67 9,18

8771 2390 1345 2789 516 77 57 2130

5 16 10 6 9.8 1.6 2.9 1,2

156400

Давление фреона, МПа: перед турбиной в конденсаторе Расход фреона, кг/с Тепловые нагрузки, МВт: парогенератора регенератора конденсатора Площадь поверхностей нагре­ва, м2:

Парогенератора регенератора конденсатора Мощность, кВт: электрическая питательного насоса циркуляционного насоса тягодутьевого устройства полезная

Температура °С Перепады температур, К:

Д;ґ Д/.

Скорости, м/с:

Отходящих газов в пароге­нераторе

Фреона в парогенераторе парообразного фреона в ре­генераторе

Жидкого фреона в регене­раторе

Охлаждающей воды в кон­денсаторе Переменная часть приведенных затрат, руб,/год

Рис. 16.2. Влияние температуры охлаж­дающей среды на величину приведенных затрат Зпр и мощность утилизационной установки N^. / — водяное охлаждение конденсатора; 2 — воз­душное охлаждение конденсатора

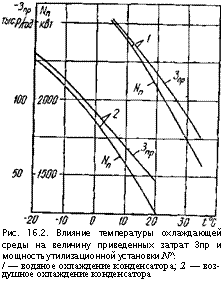Рассматривались также утилизационные установки с воздушным охлаждением конденсатора. На рис. 16.2 представлены зависимости влияния температуры ох­лаждающей конденсатор во­ды и воздуха на переменную часть приведенных затрат и полезную мощность установ­ки.

Особенно существенно влияние температуры ох­лаждающей среды на техни­ко-экономические показате­ли утилизационной установ­ки. Значительны резервы по­вышения мощности устано­вок с воздушным охлажде­нием конденсатора в холод­ный период года.

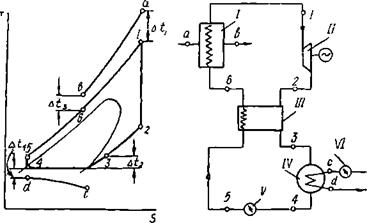
Получены зависимости (рис. 16.3), характеризую­щие рентабельность утили­зационных установок от конъюнктурных факторов: стоимости замещаемой электроэнергии в данном экономическом районе; стоимости рабочего тела, которая во многом зависит, например, от объема его производства; эксплуатационного фактора — вре­мени работы установки, которая может зависеть от периодич-

Ности выхода БЭР в основной установке. Приведенные основ­ные технико-экономические показатели утилизационной установ­ки позволяют сделать вывод о целесообразности такого на­правления утилизации тепла отходящих газов технологических агрегатов.

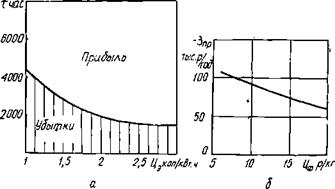
Ниже представлены распечатка ФОРТРАН-программы, не­которые рекомендации к использованию программы на ЭВМ ЕС-1033 и блок-схема программы прямого расчета параметров утилизационной силовой установки (см. рис. 16.4).

Рис. 16.3. Оптимизация параметров утилизационной установки: А — влияние стоимости замещаемой электроэнергии и числа часов работы установки в году на рентабельность; б — влияние стоимости рабочего тела на приведенные затраты

Основные обозначения (идентификаторы) программы:

/1—/6 — энтальпия точек цикла, кДж/кг;

S1—энтропия пара на входе в турбину, кДж/(кг-К);

Т — Тб температура точек цикла, °С;

ТКН, ТК1—температура конденсации, °С;

G, GB — расходы фреона и воздуха, кг/с;

Ql, Q2, <33 — тепловые нагрузки на теплообменные аппараты, кВт;

DT1, ТР — среднелогарифмически и температурный напор в парогенера­торе, регенераторе, К; fl, F2, F3 — активные поверхности теплообмена в парогенераторе, реге­нераторе, конденсаторе;

!

ДП, N2, N3—количество и длина труб, число ходов в парогенераторе, ill, Z.21, Z.31 регенераторе и конденсаторе;

Zl, Z2, Z3

NE, NB, NPH— эффективная и электрическая мощность питатального насоса, NH, ND вентилятора и дымососа, кВт,

FPC — количество фреона в установке, кг;

С1, С2, С З, С4 — стоимость парогенератора, регенератора, конденсатора и фреона, руб..

СП, С9, СЮ — стоимость турбогенератора, питательного насоса, вентилятора^ руб.;

К — переменная часть приведенных затрат, руб./год.

Некоторые рекомендации по использованик' программы на ЭВМ ЕС-11)33. Программа набивается на перфокартах. Структура формирования колоды перфокарт следующая:

Управляющие перфокарты Программа

/*

// 00. БУЗ/М-- оо~ *

Исходные данные /*

//

Определение Теплойы* Нагрузок

-А2 J-------------------- Определение мощности оспо - погателонь/х устройстЬ

_ Е2 J___________ Определение Стоимости Одорудобания

Г - А2 Определение тепл оризических сбойстб рабочем тела _ Г - В2 Определение Гидравлических Сопротивлений

І

Г - С2 Определение мощности турдина/

©

Определение рас под а фреона ГТГТЕШИ

Г - Я Определение расхода 6оз дул о

_ Р2 J_______ Определение Приведенных Затрат

_ г/ и______________________ Определение поверхностей тепл оо5меннико6 мае с ы

Г~ Я2 Печатать

_ ні J__________

Определение

Геометрических

Размеров

Теплообменников

(ЯЕТиМ

Рис. 16.4. Блок-схема подпрограммы прямого расчета параметров утили­зационной силовой установки

Оператор ввода с меткой «10», расположенный на 13-й карте по порядку, и содержащий константу ИС1 может быть заменен в зависимости от конкретной задачи, например, на «QREAD2, ИС8». Соответственно заменяются и карты с числовыми значениями в исходных данных (карты после 00. БУБШ —■£) О ^ [5]) Программа составлена так, что имеется возможность производить несколько (/) оптимизационных расчетов при изменении входных параметров. В программе используется подпрограмма М2 01 — вычисление безусловного минимального значения функции многих переменных методом прямого поиска из библиотеки стандартных подпрограмм.*

Для работы этой подпрограммы необходимо задать начальные значения

Величин и их приращений, с помощью которых определяется функция цели К в подпрограмме.

Они располагаются в трех массивах X, О, ОМ и имеют следующие значения:

X	D	DM
220	2,0	0,5
5,0	1,0	0,5
10,0	1,0	0,5
10,0	1,0	0,5
6,0	1,0	0,5
2,0	0,1	0,05
9,5	0,1	0,05
1,0	0,1	0,05
2,0	0,1	0,05
10,0	0,1	0,05
3,0	0,1	0,06

Программа оптимизации параметров утилизационной установки DIMENSION KOD (6), X (11, 3), FX (3), D (11), DS (11),

* РЕ (34, 7), XI (11), DM (11), РЕ1 (34), РК (7)

PEAL К, NE, NPH

EXTERNAL OUT1, F

COMMON J, U Cl, UC2, UC4, UC5, UC6, UC6, UC7,

UC8, UC9, UC11, Dl, D2, D3, D4, D5, D6, D7, D8 COMMON /Р1/ NE,’ FI, F2, F3, NPH, NH, ND, FRC,

ТКН, T2, T21, T6, G, GB, Ql, Q2, Q3, DTI, TP, TK,

N 1,N2, N3, LI, L2, L3, Cl, C2, C3, C4, C5, C7, СЮ, C8 EQV1 VALENCE (PEI (1), NE)

3 FORMAT (IX, 'J=', 14)

10 FORMAT (32X', ВЛИЯНИЕ ТЕМПЕРАТУРЫ ОКРУЖАЮЩЕГО

* ВОЗДУХА' ///

* 9Х, 'T = — 30',ilX,'T —20', ИХ, 'Т=—10', 12Х, 'Т = 0',

* 12Х,'Т= 10', 12Х, 'T =20', 12Х, 'Т = 30' //)

2 0 FORMAT (2Х, 7Е16.6/)

3 0 FORMAT (8F5.0)

4 0 FORMAT (IX, 11F4.1)

5 0 FORMAT (5Х, 'X =', 11F8.2/)

100 FORMAT (IX, 11F8.3)

2 0 0 FORMAT (F6.0)

J =0

READ 40, D, DM, X 1

READ 30, UC2, UC4, UC5, UC6, UC7, UC8, UC9, UC11

DO 502 II = 1,7 READ 200, UC1 M= 1 N=11 KOD (1) = 3 KOD (2) = 1 KOD (4) = 500 KOD (5) = 50 EST (6) = 0.01 DO 1 IK= 1,11

1 DS (IK) = DM (IK)

DO 2 I = 1,11

2 X(I,1) = X1 (I)

CALL F (XI, K, G, M)

FX (1) = К

CALL MINOl (KOD, N, X, FX, D, DM, DS, EST, F,

* MINLN, OUT1, A, B, IER)

PRINT 3, J

PRINT 50, X DO 501 J1 = 1,34 50 1 pe (Jl, II) = PEI (Jl)

502 рк (II) = К

PRINT 10 PRINT 20, PK

PRINT 20, ((PE (J2, 12), 12= 1,7),

* J2= 1,34)

STOP

END

SUBROUTINE F (X, K, Gl, M)

DIMENSION X (11), Gl (11)

REAL Jl, J2, J21, J22, J3, J4, J6, N1, N2, N3, N21,

* N22, N31. LI, L2, L3, LI 1, L21, NE, NB, NPH, NH,

* ND, NB1, MJU4, MJU1, К

REAL С (25)/0.01037, 0.4011, 11.832, 0.79, 0.447,

* 0.287, 353.2, 273., 188.8,2.88,6.65, 0.0125,

* 0.003457,0» 2421, 674., 0.7492E-5, 0.651 IE-3,

* 1.5304, 614., 0.648, 0.853, 0.0014; 0.823, 0.235/

COMMON J, UC1, UC2, UC4, UC5, UC6, UC7, UC8,

* UC9, UC11, Dl, D2, D3, D4, D5, D6, D7, D8

COMMON /Р1/ NE, FI, F2, F3, NPH, NH, ND, FRC,

* ТКН, T2, T21, T6, G, GB, Ql, Q2, Q3, DTI, TP, TK.

* N1. N2, N3, LI, L2, L3, Cl, C2, C3, C4, C5, C7, СЮ, C8

С ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЦИКЛА

J1 = 374.97 + 2.8392 * X (1) — 5.7227Е-3 * X (1) * * 2 +

* 0.63823Е-5 * X (1) ** 3

SI = 0.73065 + 0.0075973 * X (1) — 1.707E-5 * X (1) ** 2+

* 0.16989E-7 * X (1) **3

TKN = UC1 + X (2) + X (5)

T2= 100 .87 *S[ ** 2+86.03 * SI -307.98-1- (TKH —30) /1.65

J2= 603.8+ 0.925 *T2

J21 = J 1 — (Jl — J2) *0.823

T21 = 1.08* J21 —651.75

J4 = 498.68+ 1.128 * TKH

T3 = TKH * X (3)

J3 = С (19) + С (20) * TKH + (С (21) + С (22) * TKH) * X(3) J6= J4+(J21— J3)

T6 = TKH + (J21 — J3) /1.25 Ql = UC4*1.075*(UC2—T6-X (4))

G = Q1 /(Jl -^J6)

Q2 = G * (J21 — J3)

Q3 = G * (J 3 — J 4)

GB = Q3 / (4.19 * X (5))

IF ((X (1) + X (4)). GT. (UC2 — 5)) GOTO 50

DT1 = (UC2—X (1) —X (4))/ ALOG ((UC2 — X (1))/X (4))

GOTO 60 50 DT1 = (UC2 — X (1)+X (4))/2 60 IF (ABS (T21 — T6 — X (3)). LT. 5) GOTO 70

TP = (T21 — T6 — X (3)) / ALOG ((T21 — T6) / X (3))

GOTO 80

7 0 TP = (T21 — Тб— X (3)) / 2

С ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ТЕПЛООБМЕННИКОВ

8 0 Al = 2140. — 3.7 * (X (1)+Т6)

RI = (1. / (Al * X (6) **0.8) + l. E-4) *3.18 4- l / (.99 *

* (13 — 0.003 * (UC2 + T6+X (4))) * X (7) ** .72) + 6.E—4 FI =QI *R1 * 1000. / (.93 * DT1)

A2= 1325.— 1,25 * (T21+T3)

IF (TKH —50) 110, 110, 120 110 PK= 1.488E-3*TKH **2 + 0225 * TKH + 1.647 GOTO 90

12 0 PK = .00218 * TKH ** 2 — .05 * TKH + 3.523 90 ROI = .0271 *((X (1) + T6)/2) **2— 14.35 * (X (1) + T6/2+2164.3 ROI 1 = 361./ ((UC2 + T6 + X (4))/ 2 + 273.)

R02 = PK * 1E5 / (37.4 * ((T21 + T3)/2 + 273))

R2 = (1 / (A2 * X (8) ** 0.8) + 1E—4) * 3.17 + I / (.99 * (6.38 +

* .0118 * (T21 + T3)) * R02 ** .72 * X (9) ** .72) + 1E—4 F2 = Q2 * R2 * 1000. / TP

TK = X (2) + X (5) / 2 ALI =C (9) +С (10) * TKH

Q = 1 / ((1 / (ALI * X (11)** .8)+ 1E—4) * 11,4 - j - 1 /(8.2*

* X (10) ** .72))

F3 = Q3 * 1000./Q С ОПРЕДЕЛЕНИЕ ТЕПЛОФИЗИЧЕСКИХ ВЕЛИЧИН R06 = С (1) * TKH ** 2 + TKH* С (2) + С (3)

R03 = 1650 — 2.63 * (TKH + Тб)

R031 = 1650 — 2 *■ 2.63 * (X (2) + X (5) + LC1)

ROB = С (7) / (UC1 + С (8))

HJU1 ((63.5 Е—10* (X (1)+Т6)** 2 — 43.Е—7 * (X (1) + Тб) +

* 766.5Е—6)) I ROI

MJU4 = 112.2Е—7 + 0.147Е—7 * (Т21 + ТЗ)

N1 = G / ( 165.1Е—6 * X (6) * ROI)

Ll = F1 / (0.145 *N1)

Zl = L1 / UC9

IF (Ll. LT. UC9) Zl= 1.

Lll = Ll /Zl

N11 = UC 4* (.229 * (UC2 + Тб + X (4)) + 125.2) , (X (7)*L11)

N2 = G / (1651E—7 * X *(8) R03)

L2 = F2/ (.145 * N2)

Z2= L2/UC11

IF (L2. LT. l'Cl 1) Z2= 1 N12= N1 * Zl / N11 N21 = SQRT (N2 * Z2)

N22 = N21 L21 =L2/Z2

N3= G* 1.Е5/ (X (11) » R06*98.)

N31 = (N3 * 2) ** .5 L3 = F3/(.05966 *N3)

Z3 = L3 / 6 L31 = L31 2

W41 = G/(R02 * L21 * 12.08E—3* N21)

С ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ

PB=(C (11) — С (12) * UC1) * X (10) ** 1.76 Р4 = 6.5 * N22 * Z3 * MJU4 **.24* R02** .76 ** (9) ** 1.76 *+(2.5 * Z3+2.5) * X (9) * Х(9) » R02/2 С МОЩНОСТНЫЁ ПОКАЗАТЕЛИ

NB = С (23) * G *(J 1 — J2 — J22)*C (24)

NB1 = G * PB1 * .001 / (R03 * .5)

NPH = G* (50 — PK) * 100/(.5 »R031) + NB1 NH = PB * GB / (ROB * 800)

ND = UC 4* Pli / (ROI 1 * 800)

NE = NB — NPH — NH — ND FR = 165.1E—6 * N1 * L1 * ROI FRT = 165.1E—6 * N2 » L2 * R03 FRK = С (6) * N3 * L3 FRC = 1.3*(FR + FRT+FRK)

С ОПРЕДЕЛЕНИЕ СТОИМОСТНЫХ ПОКАЗАТЕЛЕЙ Cl = 0.625 * 6.122 * FI/0.7 C2= 14.517 * F2 C3 = 7* F3 C4 = UC7 * FRC C5 = UC6 * NE C6 = 26 * NH C7 = UC8 * NB ** 0.4 C9 = 26. * NPH CIO = 28. * ND ** 0.4

Cil = C1 +C2 + C3 + C6 - f C7 + C9 + C10 C8= 1.25* Cl I + C4 CB = UC5* GB K=C8 *C (25)—C5 + CB J = J + 2

6 RETURN END

Для решения оптимизационных задач с привле - чением экономических критериев качества применительно к теп­лотехническим системам необходима оценка стоимости энерго­носителей (топливо, электроэнергия), а также различного вида теплоносителей, рабочих тел в зависимости от различных фак­торов, действующих в настоящее время и предполагаемых в будущем. Прогноз изменения цен на топливо, электроэнергию, воду представляет особый интерес при учете экономических фак­торов в схемах с установками, выпуск или работа которых предполагается в перспективе через 5—10 лет.

Топливо. Наблюдается удорожание традиционных органи­ческих топлив — угля, нефти, газа. Постепенный переход к до­быче на менее выгодных месторождениях, приводит, например, к ежегодному росту цен на нефть на 4—7 % при их удвоении через каждые 10—15 лет.

Большое значение приобретает стоимость замыкающего топ­лива. Например, вовлечение в топливный баланс использования ВЭР приводит к сокращению общей потребности в топливе, что позволяет перераспределением топливных ресурсов исключить из баланса наименее экономичное замыкающее топливо. Его стоимость определяется с учетом затрат на транспорт, хранение и распределение (табл. 16.3).

Электроэнергия. Существенные улучшения технико-экономи­ческих показателей работы энергетического оборудования по­зволило за период с 1946 по 1966 год уменьшить себестоимость электроэнергии вдвое. Последующие годы также характеризу­ются значительным прогрессом в большой энергетике. На теп­ловых электростанциях около 70 % затрат на производство энергии составляют затраты на топливо,, поэтому одним из ос­новных факторов, воздействующих на снижение себестоимости, является экономия топлива. Удельный расход топлива на ТЭС СССР составлял в 70, 75 и 80 гг.. соответственно 366, 340 и 328 г/(кВт-ч) отпущенной электроэнергии. На 1985 г. предус­матривается дальнейшее снижение удельного расхода топлива до 319 г/(кВт-ч).

Производственная себестоимость 1 кВт-ч, отпущенного с шин электростанций в 1975 и 1980 гг. составила соответственно 0,676 и 0,657 коп., в том числе в.1980 г. по ТЭС — 0,754 коп. и по ГЭС гтт 0,146 коп. Полная себестоимость 1 кВт-ч (с учетом транспорт­ных, общесистемных и других расходов) или себестоимость у потребителя составила 0,98 коп. [105]. Однако введение повы­шенных цен на топливо и материалы с 1984 г. значительно увеличит и себестоимость вырабатываемой электроэнергии.

Для расчетов экономического эффекта могут быть использо­ваны специально разработанные показатели — замыкающие затраты на электроэнергию (табл. 16.3). Они учитывают замыка­

Ющие затраты на топливо, связанные с его удельным расходом на замыкающей электростанции, капитальные затраты, услов­но — постоянные издержки по эксплуатации и некоторые другие затраты (табл. 16.4) -

16.3. Замыкающие затраты на электроэнергию (предварительная оценка), руб./(МВт. ч) [24] Энергосистемы Годовое использование максимума нагрузки потребителей» ч 6500—7000 3000—4000 1000 Центр, Северо-Запад, Юг, Среднее Поволжье 15—16 22—24 37—40 Северный Кавказ, Закавказье 15—16 21—24 21—24 Урал 15—16 18—21 33—36 Сибирь 9—12 12- -13 Казахстан 10—12 16- -17 Средняя Азия 12—13 11- -14 Дальний Восток 14-15 16- -18

Теплоносители. Их стоимость зависит от вида теплоносителя. Для обогрева теплообменных аппаратов часто используют во­дяной пар, горячую воду, в некоторых случаях — высокотемпе­ратурные теплоносители. Универсальным охлаждающим тепло­носителем является вода. В холодильных и некоторых других энергетических установках применяются низкокипящие вещест­ва, например фреоны. Рассмотрим учет затрат на теплоносители.

Тарифы на теплоэнергию дифференцируются по энергосисте­мам и в зависимости от параметров теплоносителя. По мере уменьшения параметров теплоносителя снижается отпускная цена. Например, если тариф острого пара из котлов принять за единицу, то при теплоснабжении паром отборов с давлением р = 0,12-ьО,25 МПа он равен 0,76, а горячей водой — 0,8. В ка­честве примера для Донбассэнерго можно привести следующие цифры (за 41,86 ГДж): горячая вода — 36,30 руб., пар при р = 0,12^0,25 МПа.— 34,50 руб. Тарифы устанавливаются исхо­дя из 100 %-ного возврата конденсата на ТЭЦ. За невозврат конденсата потребители должны вносить дополнительную пла­ту— это примерно 10—15 % платы к тарифу.

Цена воды зависит от того, используется ли вода одно­кратно или многократно. В первом случае цена равна себестоимости, если вода забирается собственной насосной из водоемов. Если вода берется из внешней сети, - ее отпуск­ная цена может изменяться в очень широких пределах. Отно­сительная стоимость пресной (прямоточной) воды в зависимости от ее обработки по отношению к стоимости оборотной воды мо­жет быть представлена следующими цифрами: оборотная вода (с использованием градирен) — 1; речная вода с фильтрова-

Район	Природный Газ	Мазут	Уголь энергетический
Северо-Запад	40—42	48—50	35—37
Мурманская область	44—46	48—50	36—38
Коми АССР	32—34		24—26
Центр	39—41	48—50	34—36
Центрально-Черноземный	39-40	48—50	33-35
Район
Северный Кавказ	35—37	49—50	32—34
Среднее Поволжье	33-35	47—49	30—32
Нижнее Поволжье	37-39	47—49	32—34
Северный Урал	28—31	47—49	25-28
Южный Урал	32—34	47—49	25—27
			23—26
Кемеровская область,	25—27	47—49	15—17 (8-10)
Алтай
Новосибирская и Томская	25—28	47—49	17—19 (12—14)
Области
Омская область	27—30	47—49	20—22 (17—19)
			13—15
Красноярский край	27—29	47—49	13—15 (6—8)
Иркутская область	21-27	47—49	14—16 (9—10)
Забайкалье	_	47—49	16—18
Амурская область	_	47—49	18—20
Хабаровский край	27—29	50-52	20—22
Приморский край	30—33	50—52	18—20
Восточная Украина, Рос­	38-40	49—50	31—33
Товская область
Западная Украина, Мол­	33—41	49—50	33—35
Давия
Белоруссия, Литва	40—42	48-50	35-37
Латвия, Эстония	41—43	48—50	36-38
Грузия	36—38	49—50	33-35
Армения, Азербайджан	38—40	49—50	35—37
Туркмения	28—30	49—50	22—24
Узбекистан	29—32	49—50	20—22
Киргизия	31—33	49—50	23—25
Таджикистан	30—32	49—50	24—26
Западный Казахстан	33-35	47—48	29—31
Северо-Восточный Казах­	30—33	47-48	16—18
Стан			10—12
Южный Казахстан	31—33	47—48	18—20
			13—15

Примечание. В знаменателе указаны данные для экибастузского угля, в скобках — для канско-ачинского.

Нием—1,75; вода из водоемов (озера, пруды) с фильтрованием — 1,2; речная вода с коагуляцией, осаждением, фильтрованием и хлорированием — 4; артезианская вода — 3,65; водопровод­ная вода — 11,5.

При использовании устройств для охлаждения оборотной воды учитывается только расход воды на восполнение потерь на охлаждающих устройствах. Следовательно, расходы на ох­лаждающую воду (в рублях за год) в общем виде можно пред­ставить уравнением:

Св = СврЦвТг» (16.39)

Где Св — расход воды, м3/ч; р — отношение расхода свежей воды к циркулирующей; Цв — стоимость воды, руб./м3; тг — время работы установки, ч/год; р учитывает испарение, разбрызгива­ние и продувку в охлаждающих устройствах. Ориентировочные значения р приведены ниже:

Работа на проточной воде без оборотного охлаждения—1; оборотное охлаждение воды в брызгальных бассейнах 0,04—0,06; в обычных градирнях 0,02=—0,04; в пленочных вентиляторных градирнях с регулярной насадкой 0,01—0,02; работа испа­рительного конденсатора 0,02—0,04.

Высокотемпературные теплоносители и низкокипящие рабо­чие тела, В ряде отраслей промышленности для высокотемпера­турного обогрева все шире применяются органические теплоно­сители, среди которых наибольшее распространение получили дифенильная смесь и дитолилметан. Эти вещества недефицитны и в значительных количествах выпускаются нашей промышлен­ностью. Стоимость дифенильной смеси — 0,85 руб./кг, а дитолил - метана (ДТМ)—0,77 руб./кг.

В холодильной технике, в последнее время и в связи с раз­витием так называемой низкотемпературной энергетики в про­мышленно разбитых странах большой интерес проявляется к низкокипящим веществам. Стоимость некоторых низкокипя - щих веществ может быть проиллюстрирована следующими циф­рами (в рублях за тонну): фреон-11 (сорт Б) — 1440; фреон-12— 1800; аммиак— 101; изоб^тан (марка В) —35.

ПРИЛОЖЕНИЕ 1. Теплоносители и область их применения в промышленных теплообменных установках Теплоноситель Температура, °С Область применения Вода 30—100 Нагревание воздуха в жилых и про­изводственных помещениях Водяной пар 100—200 Нагревание и выпаривание растворов в технологической аппаратуре Минеральные масла 150—250 Нагревание веществ в дистилляцион - ных установках Высокотемпературные ор­ганические теплоносители 250—350 Нагревание смесей при дистилляции и ректификации Расплавы солей 300—500 Нагревание веществ в процессах ор­ганического синтеза Жидкие металлы (ртуть, щелочные металлы) 300—600 Теплообменные процессы в химичес­ких реакторах и установках-утилиза­торах Дымовые газы (продукты сгорания органического топлива) 200—1000 Термическая обработка материалов в барабанных печах и аппаратах с ки­пящим слоем, сушильных и плавиль­ных установках Газы (воздух, азот, кисло­род, углекислый газ, ар­гон, водород, гелий и ДР-) От —256 до + 1000 В установках пиролиза, термической обработки изделий, сушки и обезво­живания материалов, криогенной тех­ники Низкокипящие вещества (ц том числе фреоны) От —75 до +30 Хладагенты в холодильных машинах и установках От +30 до +500 1 В утилизационных силовых установках

2. Теплофизические свойства дымовых газов, полученных при сжигании природного газа ^Юлм. т химического состава (/’==0,1013 МПа)

Г °С	(> Кг/М 3	КДж/(кр К)-.	* І02 Вт/(м К)	10* ыг/а
00	1,295	1,043	2,28	12,20
100	0,950	1,068	3,12	21.54
200	0,748	1,097	4,00	32,8
300	0,617	1,122	4,83	45,81
400	0,5255	1,151	5,68	60,38
500	0,457	1,185	6,54	76.30
600	0,405	1.214	7.44	93,61
700	0,363	1,239	8.25	112,10
800	0,330	1,264	9,15	131.80
900	0,301	1,290	9,98	152,50
1000	0,275	1.306	10,90	173,40
1100	0,257	1,323	11.75	197.10
1200	0,240	1.340	12,62	221.00
1300	0,230	1,360	13.61	239,00
1400	0.220	1,380	14,40	257,00
1500	0.210	1,41	15,3	279,00
1600	0.200	1,44	16,2	300.00
1700	0,195	1.46	17,06	331,00
1800	0.190	1.48	18,1	361,00
1900	0,185	1,50	18,95	390,00
2000	0,180	1.52	19,85	419,00

3.

0,72 0,69 0,67 0,655 0,64 0,63 0,62 0,61 0,60 0,59 0,58 0,57 0,56 0,554 0,543 0,54 0,534 0,553 0,560 0,570 0,576

'кип КДж/кг 856,6 855,4 19 594 296 2076,7 4208

Удельная теплоемкость Ср при Теплопрбводность X при 500 °С.

Теплофизические свойства жидк ометалличе<чких теплой осителей

Теплоноси­ Тель	При атмосферном давлении 0,1 МПа
Р Кг/м»	(пл °С	<5	£ Ь, * • 4 Ц ^ *	X** Вт/(м К)	Гпл «Дж,
Свинец	11 350	327,4	1737	0,155	15,48	24,>
Висмут	9 830	271,0	1477	0,159	16,3	50,5;
Литий	534	180,5	1336	4,40	47,6	(;61,^
Ртуть	13 546	—38,9	357,3	0,138	13,28	11,>
Калий	870	63,7	760	0,762	34.9	61,1
Натрий	975	97,8	883	1,46	64,0	1134

'С.

ІО-5 Па	Р" кг/м	Г кДж/кг	Г кДж/кг	Ср КДж/(кг К)
0,0061	0,00485	2501,0	2501,0	1,86
0,0123	0,00940	2519,4	2477,4	1,86
0,0234	0,0173	2537,7	2453,8	1,86
0,0424	0,0304	2555,9	2430,2	1,87
0,0737	0,0512	2574,0	2406,5	1,88
0,1234	0,0830	2591,8	2382,5	1,91
0,1992	0,130	2609,5	2358,4	1,93
0,3116	0,198	2626.8	2333,8	1,96
0,4736	0,293	2643,8	2308,9	1,98
0 7011	0,423	2660,3	2283,4	2,02
1,013	0,597	2676,3	2257,2	2,14
1,43	0,826	2691,4	2230,0	2,18
1,98	1,121	2706,5	2202,8	2,21
2.70	1,496	2720,7	2174,3	2,26
3,61	1,966	2734,1	2145,0	2,32
4,76	2,547	2746,7	21 14,3	2,40
6,18	3,258	2758,0	2082,6	2,48
7.92	4,122	2768,9	2049,5	2,58
10,03	5,157	2778,5	2015,2	2,71
12.55	6,397	2786,4	1978,8	2,86
15,55	7,862	2793,1	1940,7	3,02
19.08	9,588	2798,2	1900,5	3,20
23,20	11,62	2801,5	1857.8	3,41
27,98	13,99	2803,2	1813,0	3,63
33,48	16,76	2803,0	1766	3,88
39,78	19,98	2801	171fr	4,16
46,94	23,72	2796	1661	4,47
55,05	28,09	2790	1604	4,82
64,19	33,19	2780	1543	5,23
74т45	39,15	2766	1476	5,69
85,92	46,21	2749	1404	6,28
98,70	54,58	2727	1325	7,12
112,90	64,72	2700	1238	8,21
128,65	77,10	2666	1140	9,88
146,08	92,76	2622	1027	12,35
165,37	113,6	2564	893	16,24
186,74	144,0	2481	720	23,03
210,53	203,0	2331	438	56,52

X 10* Вт/(м К)	В-10* м'/с	10« Нс/м*	10* м*/о	Рг
1,61	1790	8,75	1805	1,02
1,69	968	9,15	973,7	1,00
1,76	548	9,50	549,4	1,00
1,84	268	9,80	766,7	1,00
1,93	201	10,30	201,4	1,00
2,01	127	10,75	129,4	1,02
2,10	83,5	11,20	86,0	1,03
2,20	56,8	11,65	58,8	1,04
2,30	39,6	11,85	41,1	1,04
2,35	27,4	11,90	29,4	1,07
2,37	18,58	12,27	20,02	7,08
2,49	13,83	12,46	15,07	1.09
2,59	10,50	12,85	11,46	1,09
2,69	7,972	13,24	8,85	1,11
2,79	6,130	13,54	6,89	1,12
2,88	4,728	13,93	5,47	1,16
3,01	3,722	14.32	4,39	1.18
3,13	2,939	14,72	3,57	1,21
3,27	2,339	15.11	2,93	1,25
3,42	1,872	15,60	2,44	1,30
3,55	1,492	15,99	2,03	1,36
3,72	1,214	16,38	1.71	1,41
3,90	0,983	16,87	1,45	1,47
4,09	0,806	17,36	1,24	1,54
4,29	0,658	17,75	0,06	1,61
4,52	0,544	18,24	0,913	1.08
4,80	0,453	18,83	0,794	1,75
5,12	0,378	19,32	0,688	1,82
5,49	0,317	19,91	0.600	1,90
5,83	0,261	20,59	0,526 0,461	2,0!
6,27	0,216	21,28	2,1.3
6,84	0,176	21,97	0,403 0,353	2,29
7.51	0,141	22,85	2,50
8,26	0,108	23,93	0,310	2,86
9,30	0,0811	25,20	0.272	3,35.
10.70	0,0581	26,58	0,234	4,03
12,79	0.0386	29,13	0,202 0,166	5,23
17,10	0,0150	33,73	11,10

Пара на линии

Насыщения

Температура <, °С	С Г СС О* X £ Ч Л (5	Плотность р кт/м*	Удельный объем о. м’/кг	Энтальпия Ь, кДж/кр	1 Теплота парообразо - 1 вания г, кДж/кг	5. У Л Н.— 8 * X Я (_ 8 % § !г « 1-С н?	Теплопроводность X, Вт/(м К)	Динамическая ВЯЗКОСТЬ (Д.-Ю“, Па с	К. и нем атическ а я вязкость V 10е, м*/с	А К Ц Я: Л _о. О 5 5 Сг
Жидкости	0 £ 1 3 я и О. V «I 55 ^	Н И О 5Й Ч; *	Насыщенного Пара	1 жидкости	О И. 0 1 А л У о. Л) я т с	% К О О А * А £	Насыщенного Пара	Жидкости	О Ь. О А; Й> 3 35 ^ о о. со та Я с
20	--	1060	—	0,943	—	12,6	390	377	1,58	0,137	4360	—	4,11	—	50
100	0,0006	995	0,035	1,005	28	156	500	346	1,88	0,126	1002	6,76	1,01	192	15
200	0,025	912	0,99	1,096	1,0	364	678	314	2,34	0,111	406	8,72	0,446	8,8	8,6
220	0,042	896	1,6	1,116	0,62	415	720	303	2,43	0,108	356	9,10	0,396	5,6	8,0
240	0,064	879	2,4	1,137	0,41	460	760	297	2,53	0,105	316	9,50	0,360	3.9	7,6
260	0,105	863	3,9	1,159	0,25	515	802	287	2,64	0,1025	282	9,86	0,326	2,5	7,2
280	0,166	845	6,1	1,184	0,165	567	845	274	2,68	0,100	253	1,03	0,299	1,7	6,9
300	■0,238	825	8,7	1,211	0,115	626	889	264	2,76	0,0965	228	1,07	0,276	1,2	6,5
320	0,332	804	12,2	1,243	0,082	682	935	254	2,80	0,0940	208	1,11	0,359	0,9	6,2
340	0,456	783	17,0	1,277	0,059	740	982	243	2,89	0,0910	191	1.15	0,243	0,68	6,0
360	0,614	761	23,0	1,314	0,044	800	1030	230	2,92	0,0885	177	1,19	0,229	0,52	5,8
380	0,815	739	30,0	1,354	0,032	860	1080	220	2,97	0,0850	161	1,23	0,218	0,39	5,6
400	1,064	709	42,0	1,410	0,024	915	1120	208	2,02	0,0825	149	1,27	0,210	0,31	5,4

6. Концентрация некоторых водных растворов, кипящих под атмосферным давлением при различных температурах, %

Реннос Вещество	101	102	103	104	105	107	110	115	120	125	140	160	180	200	220
Сг. С12	5,66	10,31	14,16	17,36	20,00	' 24,24	29,33	35,68	40,83	45,80	57,89	68,94	75,85	_	_
КОН	4,49	8,51	11,97	14,82	17,01	20,88	25,65	31,97	36,51	40,23	48,05	54,89	60,41	64,91	68,73
КС1	8,42	14,31	18,96	23,02	26,57	32,62									—
К2С03	10,31	18,37	24,24	28,57	32,24	37,69	43,97	50,86	56,04	60,40
KN03	13,19	23,66	32,23	39,20	45,10	54,65	65,34	79,53
MgCI2	4,67	8,42	11,66	14,31	16,59	20,32	24,41	29,48	33,07	36,02	38,61	—	—		—
MgS04	14,31	22,78	28,31	32,23	35,32	42,86									—
NaOH	4,12	7,40	10,15	12,51	14,53	18,32	23,08	26,21	33,77	37,58	48,32	60,13	69,97	77,53	84,03
NaCl	6-19	11,03	14,67	17,69	20,32	25,09	—
Na NO,	8,26	15,61	21,87	27,53	32,43	40,47	49,87	60,94	68,94	—		—	—		—
Na2S04	15,26	24,81	30,73	—	—	—	-	—	—		—	—	—		—
Na2C03	9,42	17,22	23,72	29,18	33,86		—	—	—	—		—	—	—	—
ZnS04	20,00	31,22	37,89	42,92	46,15	—	—	—	—	—	—		—	—	—
Nh4no3	9,09	16,66	23,08	29,08	34,21	42,53	51,92	63,24	71,26	77,11	87,09	93,20	96,00	97,61	98,84
Nh4ci	6,10	11,35	15,96	19,80	22,89	28,37	35,98	46,95	—		—	—
(nh4)2so4	13,34	23,14	30,65	36,71	41,79	49,73				—	—		—
CuS04	26,95	39,98	40,83	44,47			—		—		—				—

Раство-

Температура кипения, °С

7. Средняя теплоемкость газов в пределах от 0 до 1500° С (линейная зависимость)

Газ	Массовая теплоемкость. кДж/(кг-К)	Объемная теплоемкость кДж/(мв К)
Воздух	С»т = 0.7088 + 0,000093 t Срт = 0,9956 + 0,000093 <	С'т = 0,9157 + 0,0001201 * Срт = 1,287 + 0,0001201 /
Н2	С«т= Ю.12 + 0,0005945 1 Срт = 14,33+ 0,0005945 /	Сот = 0,9094 + 0,0000523 1 срт= 1,28 + 0.0000523 (
N.	Сот = 0,7304 + 0,00008955 < Срт = 1,032 + 0,00008955 (	С;т = 0.9131 +0,0001107 Срт = 1,306 + 0.0001107 (
02	Сот = 0,6594 + 0,0001065 ( Спт — 0,919 + 0,0001065 г Рт 1 1	Сот =* 0,943 + 0,0001577 г срт= 1.313 + 0,0001577 t
Со	С„т = 0,7331 + 0,00009681 1 Срт = 1,035 + 0,00009681 t	С'т = °,Э173 + 0,°00121 1 с'рт = 1.291 + 0,000121 г
Нго	Сот= 1,372 + 0,00031 111 1 Срт = 1,833 + 0,0003111 1	Сот = 1,102 + 0,0002498 < Срт = 1,473 + 0,0002498 *
•м О О	Сьт = 0,6837 + 0,0002406 t Срт = 0,8725 + 0,0002406 1	С'т = 1,3423 + 0,0004723 / С'т =1,7132+0,0004723 *

8. Допустимые скорости газов и паров в теплообменниках, м/с Давле­ние в кор­пусе аппа­рата, МПа Молекулярная Масса 18 29 44 100 200 400 0,17 36 25 21 15 12 10,5 0,45 18 15 12 9 7 6 0,80 15 12 9 7 ’ 5,5 5 3,6 10 8,5 6 5 4 3,5 7,0 9 7,5 5 4 — -

Здесь А, А[—коэффициенты, зависящие от давления и опреде­ляемые по рис. 12.12, 12.13; — температура насыщения при

Давлении в деаэраторе; /пх, /пых—температура воды на входе в отсек и выходе из него; <10 — длина и диаметр струй в отсеке; оуо, «и,, — средняя скорость воды и пара.

Уравнения (12.11)—(12.13) содержат неизвестные величины ю0, и искомую неизвестную температуру воды на выходе из отсека (на нижней тарелке) /вы Поэтому для расчета необходимо в пер­вом приближении задать величины хшп, хш0. Обычно для верхнего отсека ориентировочно принимают = 0,51 м/е. Для задания скорости воды в струях предполагается, что при номинальной гидравлической нагрузке гидростатический столб жидкости на тарелке /гР. с = 0,06 - г - 0,08 м. Тогда скорость воды на выходе из тарелки

[1] • 0,004 • 10я

44,5 ЗОЛ 10_6

И>с = ащг ]^2^/1г (12.14)

Где |ап — коэффициент расхода; а, — коэффициент, учитывающий движение воды на тарелке.

[3] Для расчета охлаждения в полых скрубберах доменного газа можно пользоваться формулой

/С = (17.1 + 400 ^ Л!*) ргюг.

[5] Математическое обеспечение EC ЭВМ, вып. 17, : 1978.— 113 стр.