Рассмотри?,? некоторые свойства процесса деформирования металла, важные для понимания механизма образования свароч - йж напряжений и деформаций.

Пусть стержень единичной длины (рис.2.3,6) под действи­ем внешней силы N укорачивается на величину, при этом возникают как упругие деформации укорочения £*к, так и

пластические (см. рис.2.3,в). При снятии нагрузки стер­

жень разгружается упруго по прямой A, Aj, , параллельной О А, в результате чего в металле исчезают упругие деформации £уК и сохраняются пластические деформации е£к, равные отрез­ку 0Аа. Стержень укорачивается на эту величину (см. рис.2.3,б, состояние Аа ). Таким образом, полная деформация t состоит из двух составляющих: упругой £е - исчезающей при разгрузке, х пластической ер - необратимой, т. е. остающейся при раз­

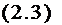
грузке :

Упругая деформация определяется по закону Гука

£е = б

£ Е 1

'равнение (2.3'' можно переписать в виде

£=т+£Р ■

Если после разгрузки вновь приложить нагрузку, но проти­воположную по знаку, то изменение напряжений подчиняется ли­нейному закону, т. е. идет по прямой АаАу По достижении пре­дела текучести (точка А3) дальнейшее удлинение стержня про­ходит за счет пластических деформаций. В момент восстадавле-

ния длины стержня (точка А],) пластические деформации удлине­ния £уд равны отрезку А^, а растягивающие напряжения дос­тигают предела текучести 6^ . При этом суммарная пластиче­ская деформация равна 4

£Ї, Ч£мк+£яд~АэА),==0А5=~£д .

Сумму пластических деформаций на любом этапе нагружения можно определить, разгружая стержень. Например, остаточные пластические деформации в металле в состоянии Aj, равны остаточным полным деформациям после разгрузки по прямой А^Ау.(состояние А 5 ). Несмотря на то что стержень восстановил свою начальную длину (полная деформация стержня в состоянии

равна нулю), в нем имеются упругие деформации удлинения £*~e, s, пластические деформации укорочения ер=-&8 , растяги - вавдие напряжения б=б5 . Если при начальном сжатии образца пластические деформации укорочения малы (|e5K|<es ), то по­

вторных пластических деформаций е. уд не возникает, а рас­тягивающие напряжения меньше 6S. Важно отметить, что при работе металла в упругой области имеет место однозначная за­висимость между напряжениями и полными деформациями, опреде­ляемая законом Гука ( 6= Ее ), в то время как при работе в упругопластической - многозначная. Так, одно и то же значе­ние напряжений б* может достигаться при различных подних деформациях е ( на рис.2.3,г), а при одной и той

же величине е, могут быть различные значения напряжений (б^б^б^ на рис.2.3,д). Это обстоятельство усложняет реше­ние упругопластических задач, так как требует изучения исто­рии деформирования рассматриваемого тела. Из рис.2.3,г, д видно, что для определения напряжений в данный момент про­цесса деформирования образца необходимо знать не только полную его деформацию в рассматриваемый момент, ьо и полную деформацию в момент начала разгрузки, т. е. характеризуемую точками AAn, Al

При учете деформационного упрочнения полная деформация также состоит из упругой к пластической частей в соответст­вии с формулой (2.4). Однако стадия разгрузки с последующей нагрузкой противоположного знака протекает для различных ме­таллов неодинаково. У некоторых металлов процесс деформиро­вания сопровождается анизотропным упрочнением (рис.2.4,а).

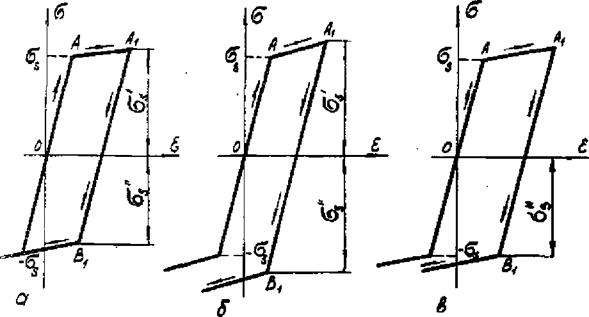при котором изменение знака нагрузки приводит к повторному пластическому деформированию при напряжении б§ , меньшем предела текучести (|бд'Кба - эффект Еаушингера); для других металлов характерно изотропное упрочнение (рис.2.4,б), при потопом повторное пластическое деформирование с изменением знака нагрузки начинается при напряжении ба, равном до аб­солютному значению <эа напряжению к моменту начала разгруз­ки Пба!=бд ); наконец, для третьей группы металлов деформа­ционное упрочнение не изменяет величины предела текучести os нагрузке противоположного знака,- приводящей к повторному пластическому деформированию (1ба1=ба ), как изображено на ' . / „а* .4, в *

Бкс.2.4. Схематизация диаграммы растяжения-сжатия

С уЧбТОМ упрочнения

Бри испытании образца, нагретого до температуры Т<Т*, г. о є приведенные рассуждения остаются неизменными, но полная дг: ..о.'мания образца увеличивается на свободную температурную деформацию ат-оСТ. Таким образом, при линейном напряженном. хоянкп полная (действительная) деформация выражается так:

*4+«р+ет

L

Как известно, стержни, работаицие на растяжение или сжатие, испытывают помимо продольных деформаций и поперечные Последние противоположны по знаку продольным деформациям и пропорциональны им.

Направим ось х вдоль оси плоского образца, а ось у - перпендикулярном направлении (рис.2.5) к введем индексы :: у соответственно для продольных и поперечных дефор-

Предположим, что вследствие какой-то причины (например, на­грева'' призма стремится удлиниться на величину Ы/ . Объемом удлинения призмы будегл называть произведение площади основа­ния призмы на абсолютное удлинение, которое она стремится приобрести:

. (2.9)

Если призма стремится укоротиться, то получим объем уко­рочения, который также определяется по формуле (2.9), но со знаком минус. Стремление призмы удлиниться (укоротиться) может быть реализовано полностью, частично или совсем не реализовано (рис.2.6,а-в), Иначе говоря, фактическое измене­ние длины призмы ДЬ в общем случае не равно М' . Размер­ность объема удлинения (укорочения) выражается в кубических сантиметрах. На рисунке штриховкой показаны объемы удлинения призмы в направлении х. Так как абсолютное удлинение (уко­рочение) равно M.,ss&xL, где ах - относительное удлинение (укорочение), которое стремятся приобрести волокна призмы, то объем удлинения (укорочения) может быть определен по формуле

AVx=FUx=Vex, (2.10)

где V=FL - исходный объем рассматриваемой призма, смР.

Итак, объем удлинения (укорочения) равен произведению площади основания призмы на абсолютное удлинение, которое она стремится приобрести, или, что то же самое, равен произ­ведению начального объема призмы на относительное удлинение (укорочение) продольных волокон, которые они приобрели бы при условии свободного деформирования. Если отнести исходную длину призмы к единице длины, то получим так называемый по­гонный объем удлинения или укорочения, т. е. объем, приходя­щийся на единицу длины (рис.2.6,г). Обозначая его irx, мож­но записать

. (2,IX)

размерность объема удлинения (укорочения), приходящего­ся на единицу длины, выражается в квадратных сантиметрах. Если в пределах площади F деформации е'х неодинаковы (рис.2.6,д), т. е. продольные волокна стремятся ‘удлиниться (укоротиться) на разную величину ^(у^к) , то

Объем удлинения (укорочения) нельзя смешивать о общим изменением объема, Так, например, при нагреве кубика с реб - х) Одного из главных направлений деформаций.

ром а общее увеличение его объема равно AVT=a?3eT (см. § 2.1), в то время как объем удлинения в любом из направле­ний в три раза меньше (рис.2.6,ж):

Av£~«J-avJ-aV - (2.га)

В качестве другого примера, иллюстрирующего разницу в понятиях общего изменения объема и объема удлинения (укоро­чения) , рассмотрим перераспределение объема металла при

пластической деформации призмы LBs. Ее объемы удлинения (укорочения) в каждом из направлений определяются произведе­нием начального объема призмы на соответствующую пластиче­скую деформацию (рис.2.6,3), т. е.

• &vJ=Ve. J •, і (2.20)

а общий объем призмы не изменяется (в соответствии с законом сохранения объема металла при пластической деформации)

AVp=Av£ + AVj+AV£=0 . (2.21)

Отеюда следует, что если в результате пластической де­формации в двух направлениях возникают объемы удлинения, то в третьем - объем укорочения, и наоборот, если в одном на­правлении йУ£=0 , то ДУу=-ЛУ£ (такое перераспределе­ние объема возможно в условиях плоского напряженного состоя­ния) . Предположим, что в направлении размера L. призма от­несена к единице длины (следовательно, ее начальный объем V0=Bs=F ), ав направлении размера s пластические де­формации не изменяются (рис.2.6,е). Тогда перераспределение

ее объема характеризуется погоннши объемами удлинения и укорочения, равными

•, vJ-sJeJiLy •, . (2.22)

ь В ' в

Интегралы в этих выражениях определяют площади эпюр пласти­ческих деформаций по ширине призмы. Обозначая их соответст­венно, s£ можно записать

xr£ = ss£ •, . (2.23)

Аналогично, при указанном условии погонные объемы удли­нения, возникающие в результате нагрева, можно выразить так:

= , (2.24)

где ST - площадь эпюры температурных деформаций (тая как йТ“ь»™ ^ АТ, то $£,=Sy*si=ST).

Сварной шов может тлеть направление вдоль и поперек оси балки. Если шов параллелен оси балки, то ее деформации зави­сят от изменения объема металла в направлений оси шва - от объема продольного удлинения (укорочения'і сварного соедине­ния, Если же шов перпендикулярен к оси балки, то ее деформа­ции зависят от изменения объема металла в направлении, пер- пендикулярном к. оси шва - от объема поперечного укорочения сварного соединения. Прежде чем определить указанные объемы при тех или иных условиях сварки, получим общие расчетные формулы для оценки параметров изгиба балки, обусловленного объемными изменениями металла.