Уравнения (7.2) и (7.3) получены Дебаем при условии, что все диполи в диэлектрике одинаковы и не взаимодействуют между со­бой, поэтому имеется одно время релаксации т. Однако в реаль­ных диэлектриках, в частности полимерах, процессам релаксации присуще распределение времен т*, описываемое релаксационным спектром. Тот факт, что диэлектрические свойства полимеров не могут быть точно описаны уравнением с одним т, был впервые принят во внимание Фуоссом и Кирквудом [7.2], которые прямым образом учли существование спектра времен релаксации для поли­меров. Учет распределения времен релаксации в конденсирован­ных системах, в которых отсутствуют дальнодействующие силы, сделан в теории диэлектрических свойств слабополярных систем. Если функция распределения времен релаксации является сим­метричной, то для обобщенной диэлектрической проницаемости может быть использовано модифицированное уравнение Дебая вида

1 £ст-е~ (7.5)

1 + (гогс)1 а

Здесь 0^а^1 (а—параметр, характеризующий ширину спектра времен релаксации). Если а=0, то мы имеем классический слу­чай (одно время релаксации); случай, когда а=1, соответствует системе с бесконечно широким спектром времен релаксации. Пара­метр а влияет на значение в максимуме и на ширину кривых е" = = е"(оо) и е" = &"{Т). Для процессов с одним временем релаксации при этом получаем

Бщах — С^ст гео)/2. (7.6)

Уравнение (7.5) в ряде случаев недостаточно точно описывает изменение поляризации диэлектриков в зависимости от со и Г, по­этому Гаврильяком и Негами [7.3] было предложено более общее уравнение, которое может быть использовано для описания процессов с асимметричной функцией распределения времен ре­лаксации:

[1 + (to*)1—]* ’

где O^p^l (р— параметр, учитывающий асимметрию функции распределения времен релаксации). Количественной характеристи­кой диэлектрических потерь является диссипация энергии W в еди­ничном объеме диэлектрика. Для неполярных диэлектриков она вы­ражается формулой вида
где а— удельная электропроводность диэлектрика, определяемая по остаточному току в постоянном электрическом поле. Для поляр­ных диэлектриков W пропорциональна коэффициенту потерь е"= = 8 tg б, квадрату напряженности Е2 и частоте со приложенного

поля:

W=v ЕЧ tg 8/(8я),

где W = 0,24rf72co8 tg б, где [/ — напряжение; с — коэффициент, об­условленный формой электрического поля (например, в случае пло­ского конденсатора с = $/ (And).

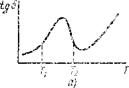
Рис. 7.3. Зависимость

tg 6 от температуры для вещества, имеющего ди - польные потери (а), и эквивалентная электри­ческая схема, модели - ч рующая такое вещест­ву во (б)