Функция <р(т)

Рассмотренный выше регенератор с постоянными температурами газа и воздуха на практике встречается чрезвычайно редко, да и то в искаженном виде. В действительности температура газа почти всегда повышается вслед­ствие увеличивающегося нагрева регенератора, а температура воздуха падает вследствие прогрессирующего охлаждения.

Выразим температуру газа следующим образом:

&г = 0го + ?(тг). (652)

Здесь &г —температура газа за время тгг, т. е. спустя г г часов после начала газового периода; $Го — температура газа в начале газового периода и Ф(тг)—функция, значение которой нужно определить.

Как и в ранее сделанных расчетах, в газовом периоде

= “г •, (аг — ®г. пов)а тг ккал/м* (653)

Или с учетом уравнений (605) и (652)

= аг • 1®г0 + * (тг) - *>г. к.ср. - / <*РИ а V <654>

Здесь для кривой изменения температуры поверхности выбрана такая же

Функция, как и по уравнению (627). Это вполне допустимо, так как она не

Зависит от точного значения величины п. Общее изменение температуры за­висит от нее в большей степени. Обозначаем общее изменение температуры через А $г. к.ср > величину которой определим в дальнейших расчетах.

Аналогично уравнению (603)

TOC o "1-5" h z а(2т = "" 2....... а ®г. к.ср. ккал/м*. (655)

Приравнивая уравнения (654)- и (655), получаем выражение

• " • <*»г. к.ср. = М8Г0 + 9 ^г. к.ср. { М<,тг

• »р.«.«. + - с. т~ и ы - * м - »го= 0. (657)

Или, раскрывая скобки и деля обе части на аг и Лх г, получим ^г. к.ср. , 2 "г й, 2 «г

Л%г С • 5 • У ГК СР - 'с ■ $ - У

2 А,

Оно, как и уравнение (608), представляет собой линейное дифференциальное уравнение первого порядка. От уравнения (608) данное выражение отлича­ется лишь тем, что вместо [(Хг ) стоит разность /(тг —Ф(тг) и вместо 0Г— значение Ого. Напротив, вместо выражения (610) появилось новое выражение

1-

С.^Т '1[Ы~Ф(Тг)1'С (658)

Так же, как и в уравнении (610), <р(тг) необходимо выразить через функцию

X

Е в форме е г, если интеграл (658) должен дать конечное решение.

Соотношение между температурой газа Ог и начальной температурой Ф 0

По уравнению (652)

&г = $г0 ф (тг).

Примем для температуры газа дополнительно

&Г = С3+С4-* * . (659)

Здесь С3, С4 и тп — постоянные, которые еще необходимо определить. Теперь надо показать, может ли уравнение (659) при правильном определении кон­стант по «краевым условиям» описать желаемую кривую изменения темпера­туры газа 0Г • Константы по «краевым условиям» определяют следующим об­разом.

Для времени тг =0 температура газа должна быть $го °С, следователь­но, по уравнению (659)

TOC o "1-5" h z йг0 = С3 + С4. (660)

Для времени тг=^г. п температура газа должна быть $Г1 °С, следова­

Тельно, по уравнению (659)

&п = Сз + С4.<?'я. (661)

Если уравнение (660) вычесть из уравнения (661), то получим

&п-»го = С4(ет - 1) (662)

Или С«= „т__________ ! • (662а)

0г1 — 9Г0 е

Следовательно, по уравнениям (660) и (662а)

С» = »го Y • <663)

еш— 1

В соответствии с этим уравнение (659) после подстановки значений С8 и С4 примет вид

Здесь 8Г1—&г0 —не что иное, как увеличение температуры газа в газо­вый период Д&г - Следовательно, по уравнению (664) температура газа для времени тг будет равна

Тг

Т -

( г. п ________

Ог = аго + даг —-------------- (665)

Н, зная уравнение (658),

Т -

Ф(т г) = С5(е ГП- 1). (666)

В этом уравнении

Д&г

Сб= т - (66?) ет—1

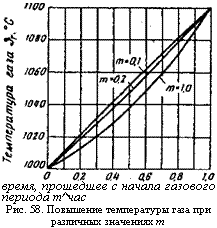
Как показали измерения и подробные расчеты, приведенные ниже, темпера­тура газа в регенераторах возрастает во времени довольно прямолинейно. Следовательно, необходимо попытаться с помощью правильно выбранной по­стоянной т приближенно описать прямолинейный характер кривой измене­ния температуры газа. На рис. 58 эта кривая дана для трех различных зна­чений т и для постоянных величин А $г= 100 °С и 0го=Ю00°С. Видно, что кривая быстро приближается с уменьшением т к прямой линии и при значе­нии т=0,1 практически совпадает с прямой линией. Следовательно, в даль­нейшем расчет нужно вести с т=0,1.

Средняя температура кирпича Фг. к.ср

Если вместо f(тг ) подставить /(тг)—ф(ті ) и вместо йг величину йго» то решение уравнения (607) будет соответствовать уравнению (608). Как и в уравнении (609) или соответственно (628), получим

TOC o "1-5" h z

Н Г 2а,

«7 || 2 аг £ч л «у 2

2 «г ттмт 2 а х

'’Г. к.ср— 1-І <**Г. П +

+ ^-[»го+<РЫ]е “Т Фг) + С, | (668)

и после подстановки / (тг ) и <р(тг) [уравнения (627)] и (666) и интегриро­вания, получаем

(1-е“?>

(і—Г23-! V 2агтг п I

2е

Т

1 — е~

Г

+ »Г0-С5+-------------- £•*----- 1!-------- + С, е С’Т. (669)

СбЧ т

Здесь Се — постоянная интегрирования. Она определяется снова из краевых условий. Для времени тг =0 средняя температура кирпича в рассматриваемой точке регенератора должна быть $пк- Следовательно, по уравнению (669)

TOC o "1-5" h z Мгкср Г 2 2 ill

»«к = — • (і - ч) • I---------- г — --------------- 11+

----------- "

~г ^го — - j - -{- Св°С. (670)

с • s • Т /л

“ЦТ '^7+1

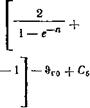Отсюда искомая постоянная интегрирования

К CD

Се = $Г1К + о (1 — ^)

2

( ■•«-т - Л,,-.-.)

V 4v. І

С 5

(671)

2 . аг

Ср

В дальнейшем это выражение сокращенно будем обозначать через Се. Средняя во времени температура поверхности кирпича Фг. пов,

Так как целью расчета является определение средней температуры. поверх­ности, то прежде всего по уравнению (626) нужно перейти к определению тем­пературы поверхности. Следовательно,

-п -

1 — *Г) / 1 — е

^г. пов ~ ^г. к.ср "Ь ^г. к.ср ' ~ “ * у2 | ^__л ^

Если в это уравнение подставить значение $г. к.ср из уравнения (669), то для температуры поверхности рассматриваемого кирпича спустя тг часа по­сле начала газового периода получим

TOC o "1-5" h z Д&г к си 1 — Ч *гп / 1

— • е------------ / 1 + °С.-------------------------- (672)

Ч 1 — € П I ri. C S - Т 1 1

2агтг. п

Средняя температура поверхности в газовый период продолжительностью ’г п дается снова по способу получения уравнения (642):

#г. ш>В. ср = 8гО-С+ с.35у ' ~(ет -!) +

Т. __------------------- + 1

2 агхг. п

2 а х Г Г. П

Тг. п ^ г

Д8Г к си 1 / 1

-—!:;5;£2--(1-1))— •/ 1 +-------------------------------------- (673)

Ч I П • с • в • Т

2 агтг. п

Значения С5 и Св определяются при помощи уравнений (667) и (671). Для воздушного периода получим следующее уравнение:

TOC o "1-5" h z ЛЭв = “в • (6в. пов — ®в)й тв ккал/м* (674)

Или с учетом уравнения (636)

*2. = “в I&в. к.Ср — / (тв) — »„] <1 тв ккал! м*. (675)

Далее, как и в уравнении (638),

<К? в = — ° * Т »в. к.ср ккал/м*. (676)

В уравнении (675) температура воздуха &в не постоянна. На основании тех

Же положений, что и в уравнении (665), температура воздуха йв после на­чала воздушного периода

9В = &во - А&в(Є--------------------- — °С. (677)

Ет — 1

Здесь снова для сокращения полагаем

». = »в0-С5(е “"-О - (678)

Следовательно,

^-*5 — ***-■. (679)

Ет-1

Обозначим

*в = »в.-*(*•>■ (680)

Тогда уравнение (675) преобразуется в выражение

^В = ав1&в. к.ср— — ав0~ <Р(тв)]‘*тв - (681>

Если уравнения (675) и (681) приравнять одно к другому, разделить все на. йх в и перенести в левую часть, то для воздушного периода получим дифференциальное уравнение

^ВКСО 2ав 2 ав 2 ав$во

-Ц?- + — • «В.,СР - [/ (тв) - 9 К)/ - -77777 - 0- «*2>

Пренебрегая индексом «в», заметим, что это уравнение отличается от (657) лишь выражением в квадратных скобках. Применяя уже известный метод, получим решение для средней температуры рассматриваемого кирпича спу­стя тв часа после начала воздушного периода

—п ■

В в. п

С5 • е

+ Ов0 + с8_-------------- с; -- т +С;-е °С. (683)

2 автв. п

Это уравнение отличается от (669) лишь знаками перед ДФв. к.сри Сб - Так как охлаждение кирпича за период равно его нагреванию, то Д^в. к.ср=Д^г. к.ср== =ДОк. ср - Поэтому в дальнейшем индексы «в» и «г» можно опустить. Тогда постоянная интегрирования

Температура поверхности рассматриваемого кирпича получается из уравнений* (634) и (683)

Пт Т®

ТП • ----

Т 2 • <Х тп

С; • в В П

TOC o "1-5" h z -* К ' " / С • 5 • 7

»в. пов~»вО+С5-- % , т + С6- +

Т'—0------- -+1

2 автв. п

"г. к.ср V1 Ч/ В. П / 1 ж

------------ # --------------- . ^ ^ (б85>

,, (1-е-п) п. с-3-т 1

2 “в • тв. п

Отсюда средняя температура поверхности рассматриваемого кирпича в воз^ душный период продолжительностью тв. п часа

С5 1

^в. пов. ср = ®в0 "Ь ^5 £ . 5 . у ‘ т 0 4"

Т •-------------- + 1

2 • “в • тв. п

2 а т

# В в. п

С6 ’ с ' в • 7 ~ с

+------------------ (1_в г) +

2 • °втв. п

Д8 / 1

(1—•Ч)/--------------- +1°С. (686>

П • 7] I Л • С • в • у

2 • а т в‘’в. п

Разность средних температур поверхности ^.пов-ср — ^в-пов-ср

Теперь можно определить разность Фг. повср— ^в. поь. ср* Ради простоты мы снова полагаем аг = ав и, сг. п = тв. п или соответственно аг*тг. п = = «в •'Св. п =ат. Это упрощение относится лишь к фактору, который отличает х от и ид* следовательно, является лишь, так сказать, поправочным коэффи­циентом, не имеющим существенного влияния. Основной коэффициент %ид который в общем составляет 80% всего значения, по-прежнему точно рассчи­тывается по отдельным коэффициентам теплоотдачи аг и ав, зная продол­жительности периодов тв. п и тг. в по уравнению (583). Если уравнение (686) вычесть из уравнения (673), то для искомой разности средних температур по­верхности кирпича в газовый и воздушный периоды получаем выражение:

TOC o "1-5" h z С* + Се ет— 1

.ср в. пов. ср ^г0 ^в0 (^5 + £5) ■

С • т • в • у т

2 агтг. п 1

+ кс.-с.)--^д - - О-Р-А+ V «®>

V 2 • *г ' тг.. /

^г. пов. ср ^в. повср ** (^го &во)(1 ^ + Сб) ^ Ет — 1_ — — 6 + —

Ч. (!-*-«)

2аг'тг. п Здесь величина #Го—^во неизвестна, но, пожалуй, можно пользоваться раз­ностью дг-ср—^в. ср» которая дана для определения <7. Следовательно, соот­ношение между средними температурами газового и воздушного периодов $г. ср и ^в-ср должно определить и соотношение Ого и #ва • Ого в газовый период увеличивается на величину ДФГ, так как пред­полагаем линейный характер распределения температур; следовательно, сред­няя температура газа ^.4.“*« + -^- °С - ’ (690)

Д*к. ср = ■

С • в • у Т • —---------- + 1

2агхг. п

Дав

°С.

2% (^Г. Ср ^В. Ср)

В. ср/

(1-ч>/ 1+е-Л +

П • С • в • 7 2агтг. п

Т

С - 5 • 7 2аг • тг. п

+ 1

/71

2 а X Г г. п

С » 5 - У 2 • “г • тг. п

С • 5 - Т

Ь =

(1-е

)•

Здесь

(688)

Если из уравнений (671) и (684) получить разность Се— С6 . и поставить <ее в уравнение (687), то получим

]

Д8к, р|‘-

1+

О—ч) , + 2---------- — 1 +• Л. 7)

(689)

Аналогично средняя температура воздуха

^в. ср ^вО '

(691) (692)

Следовательно,

-(Д»г + Мв).

Г. ср в. ср

Коэффициент теплопередачи регенератора с переменными температурами газа и воздуха

По уравнению (648)

(693)

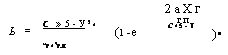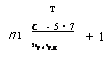П —— Ч Г. пов. ср ^в. пов. ср.

О о ^г. ср в. ср

= 1 — 6 —

(^-0(»г. ср-^.ср)

X

Если уравнения (692) и (693) подставить в уравнение (689), тЬ, наконец, получаем соотношение Да + д& Г ' в

(694)

Здесь по уравнениям (667) и (679) подставлено

, Д§г -|- Д$в 5 5 ~ -;т _ ,.. • (695)

Если, как и в уравнении (650а), в левую часть уравнения (694) вместо

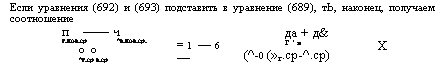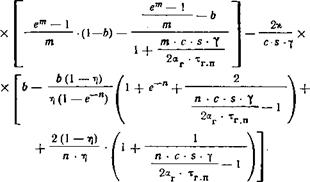
- подставить выражение 1-

■и решить относительно

^Г. пов. ср ------ ^в. пов. ср

^Г. ср ^Р. ср

*ИД

Х, то получим искомый коэффициент теплопередачи периода в случае реаль­ного регенератора

5

Ет — 1

Т - с 8 Ч 2'аг'хг. п

1 +

Е”7 — 1 т

(1 -6)-

Д0Г -}- Д0В
(^-•)(&г. ср-9в. ср)

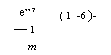1 +

Б--^Ь/1 + е-"+

Лид

Г г. п

(696)

Ккал/мг-пер°С.

+ -^/і+-

П У1

Выше былб найдено, что изменение температуры газа и воздуха тем больше приближаемся к пря'мой^чём меныпё будет т. Для т^О, 1 кривая температу­ры практически не отличается от прМЫк'4 Э8).

И умножить числитель и знаменатель на *Ид = Д&г "4“

1

= 1,05.

Т

6 + 9,52-

О ___ о Г. ср в. ср

Ь---------------- —/!+«"" + ■ Т)(1-е-п)

ПС 8^ 2ат тг. п

Для 7П=0,1
Ет— =0,105;
Если это значение и величину /л=0,1 подставить в уравнение (696) А • т То получим
1,05 — 6
	1,05(1-6)-
С • $ . У 2а • т_ _ г г. п
1+0,1
Лид
1 —	, +

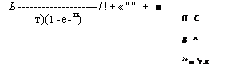+ п'-* П. Т]

П • С • 5 • 7 ^аг * тг. п

Ккал/м2-пер-° С. (697)

Для значений я>4 величина г п будет пренебрежимо мала. Для вышепри - нятого значения п—-8 уравнение (697) принимает вид

1.05 * I — •»-

С-* • Т 2а-г „

Ккал/.и* пер ’С. 1693)

^9.52

»гср-».ср

1,05 - Ь

I 0,1

I - - С-1 т

С • * • т

С 8-У 2аг • тг. п

6 =

Здесь:
(1-е	(699)
Влияние изменения температуры газа и воздуха на коэффи­циент теплопередачи. Уравнение (698) отличается от выраже­ния (651), выведенного для к при условии постоянства темпе­ратур газа и воздуха, лишь слагаемым 5 в числителе. Следо­вательно, это слагаемое 5 отражает влияние изменения темпе­ратуры газа и воздуха во времени.

Возникает вопрос, как велико это влияние и не появляется ли неучтенной ошибки вследствие предположения о прямоли­нейном характере увеличения температуры газа или соответст­венно падения температуры воздуха. Так как знаменатели в - уравнении (696)—переменная температура газа и воздуха — и в уравнении (651) —постоянная температура газа и воздуха равны, то лучше всего отклонение характеризовать соотноше-

Перемен

Ь+я

Время, прошедшее с начала газового периода т^час Рис. 58. Повышение температуры га­за при различных значениях т

Нием

Впостоян

При обычных условиях Ь равно примерно 0,5. Кро­ме 6, 5 зависит еще от т и Д9Г + ДНВ ^

——Е—- Эта послед-

*г-ср — $в. ср

Няя величина также при­мерно равна 0,5. Если для т положить значение 0,1, то Ь -(-5

—= 1,07. Коэффициент

О

Теплопередачи при прямо­линейном увеличении тем­пературы газа будет, следо­вательно, на 7% больше, чем при постоянной темпе­ратуре газа или воздуха.

Получим лишь по сравнению

Ьсли же взять т = 1 с со­ответственно вогнутой кривой по рис. 58, то

Л + 5

Очень небольшое изменение:

Дйг + Д»в

С 1,07. Из этого следует, что коэффициент теплопередачи прак­тически не зависит от т в данной области.

Если же для

Положить очень высокое

^г*ср ^в. ср

Значение, равное 1, то вышеназванная величина увеличится на 13 и 14% или соответственно она будет равна 1,13 и 1,14 вместо 1,07 и 1,065- Следовательно, в этой области влияние т также невелико (1,13:1,14 = 0,991). При этом необходимо еще учесть, что, как показали упомянутые выше измерения, проведенные в каупе'ре, температуры газа и воздуха фактически изменяются по линейной зависимости от времени (но то же самое ни в коем случае не. справедливо для температуры кирпича). Примерно линейный характер этого изменения подтверждается также уравнениями, выведенными для температурного перепада.

Из цифр/ приведенных выше, можно сделать вывод, что ко­нечное уравнение (698) дает ошибку, вызванную величиной т, 24*
равную примерно 1%. К этому надо еще добавить ненадеж­ность вследствие выбора п, которую можно оценить +~2% [ср. с уравнением (286)], так^то общая ошибка по уравнению (698) ие может превышать + 3% при примерно равных значениях

^ 'п ^ ^в-п[192]

Прежде чем перейти к анализу уравнений (697) и (698), необходимо выяснить вопрос определения Дуг и Дув. Эти вели­чины выражают увеличение температуры газа и уменьшение температуры воздуха во времени в рассматриваемой точке ре­генератора.