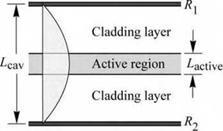
The basic structure of an RCLED is shown in Fig. 15.1 and comprises two mirrors with reflectivity R1 and R2. The reflectivity of the two mirrors is chosen to be unequal so that the light
exits the cavity predominantly through one of the mirrors. This mirror is called the light-exit mirror. Here we designate the mirror with reflectivity Ri as the light-exit mirror. An active region is located between the mirrors, preferably at the antinode location of the standing optical wave of the cavity, as shown in Fig. 15.1. Metal mirrors are assumed in Fig. 15.1 so that the wave amplitude is zero at the location of the mirrors.

Fig. 15.1. Schematic illustration of a reso­nant cavity consisting of two metal mirrors with reflectivity and Rj - The active re­gion has a thickness /-active ar>d an absorp­tion coefficient a. Also shown is the stand­ing optical wave. The cavity length Z, cav is equal to X/2.

Next, we summarize several design rules intended to maximize the spontaneous emission enhancement in resonant-cavity structures (Schubert et al., 1994, 1996; Hunt et al., 1995a, 1995b). These rules will provide further insight into the fundamental operating principles of RCLEDs and the differences of these devices with respect to VCSELs.

The first design criterion for RCLEDs is that the reflectivity of the light-exit reflector, R1, should be much lower than the reflectivity of the back reflector, i. e.

R1 << R2 . (15.1)

This condition ensures that light exits the device mainly through the reflector with reflectivity R1. Equation (15.1) applies to the design of communication RCLEDs, where light is emitted into the small core of a multimode fiber, and display RCLEDs, where light should be emitted towards the observer.

The second design criterion calls for the shortest possible cavity length Lcav. In order to derive this criterion, the integrated enhancement, discussed in a preceding section, can be rewritten by using the expressions for the cavity finesse F and cavity quality factor Q. One obtains

Gn = І - 1 1 IR1" ІС» (15.2)

2 n 1 д/R1R2 A n Lcav т

where X and Xcav are the active region emission wavelengths in vacuum and inside the cavity,
respectively. Since the emission wavelength X and the natural linewidth of the active medium, AXn, are given quantities, Eq. (15.2) shows that minimization of the cavity length Lcav maximizes the integrated intensity.

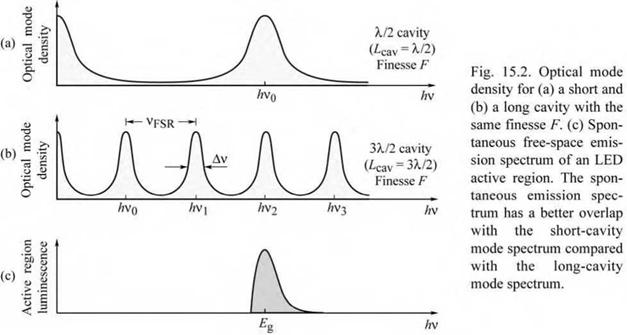
The importance of a short cavity length is elucidated by Fig. 15.2. The optical mode densities of two different cavities, namely a short and a long cavity, are shown in Figs. 15.2 (a) and (b), respectively. Both cavities have the same mirror reflectivities and finesse. The natural emission spectrum of the active region is shown in Fig. 15.2 (c). The best overlap between the resonant optical mode and the active region emission spectrum is obtained for the shortest cavity.

The largest enhancements are achieved with the shortest cavities, which in turn are obtained if the fundamental cavity mode is in resonance with the emission from the active medium. The cavity length is also reduced by using a DBR with a short penetration depth, i. e. a DBR consisting of two materials with a large difference in the refractive index.

The third design criterion is the minimization of self-absorption in the active region. This criterion can be stated as follows: the reabsorption probability of photons emitted from the active region into the cavity mode should be much smaller than the escape probability of photons through one of the reflectors. Assuming R2 ~ 1, this criterion can be written as

2 Lactive < (1 R1)

where a and Lactive are the absorption coefficient and the thickness of the active region, respectively. If the criterion of Eq. (15.3) were not fulfilled, photons would most likely be reabsorbed by the active region. Subsequently, re-emission will, with a certain probability, occur along the lateral direction (waveguided modes), i. e. not into the cavity mode. Another possibility is that the electron-hole pairs generated by reabsorption recombine non-radiatively. In either case, reabsorption processes occurring in high-finesse cavities reduce the cavity mode emission out of the cavity. Thus, if the condition of Eq. (15.3) is not fulfilled, the emission intensity of resonant cavities is lowered rather than enhanced.

20

Fig. 15.3. Spontaneous electroluminescence spectrum of a vertical-cavity surface-emitting laser (VCSEL) emitting at 850 nm and of a resonant-cavity light-emitting diode (RCLED) emitting at 930 nm. The drive current for both devices is 2 mA. The VCSEL spectrum is multiplied by a factor of 10. The threshold current of the VCSEL is 7 mA (after Schubert et al., 1996).

Whereas the condition of Eq. (15.3) is fulfilled in RCLEDs, it is clearly not fulfilled in VCSELs. The spontaneous emission intensities of RCLEDs and VCSELs were compared by Schubert et al. (1996). In this comparison, the VCSEL and the RCLED were driven by an injection current of 2 mA, which is below the threshold current of the VCSEL of Ith = 7 mA. The spontaneous emission spectra of an RCLED and a VCSEL are shown in Fig. 15.3. The VCSEL has an AlGaAs/GaAs quantum well active region emitting at 850 nm. Both reflectors of the VCSEL are AlGaAs/AlAs DBRs. Figure 15.3 reveals that the emission intensity of the VCSEL in the spontaneous regime is more than a factor of 15 lower than the emission intensity from the RCLED.

Because the magnitude of the maximum gain in semiconductors is always lower than the magnitude of the absorption coefficient in an unpumped semiconductor ( | g | < | a | ), VCSELs could not lase if the condition of Eq. (15.3) were met. Thus, the spontaneous emission intensity in VCSELs is low and must be low in order to enable the device to lase. Figure 15.3 also reveals that the emission spectral linewidth of VCSELs is narrower than that of RCLEDs. The higher spectral purity is due to the higher values of R1 and R2 as required for VCSELs.

The fulfillment of Eq. (15.3) by RCLEDs also implies that these devices cannot lase. As stated above, it is always | g | < | a |. Consequently, the mirror loss (1 - R1) is always larger than the maximum achievable round-trip gain (2 £ g Lactive). The fundamental inability of RCLEDs to lase has been verified experimentally by pulsed injecting currents of large magnitude without finding any evidence for lasing. These considerations show that the device physics of RCLEDs and VCSELs is fundamentally different.

The arguments used above imply that the spontaneous emission into the fundamental cavity mode in VCSEL structures is very low due to reabsorption of photons by the active region. A reduction of the threshold current by increasing the reflectivity will be accompanied by a further decrease of the spontaneous emission below threshold. We therefore conclude that the so-called zero-threshold laser (Kobayashi et al. 1982; Yokoyama, 1992) cannot be realized by a planar resonant-cavity structure.