РАСПРОСТРАНЕНИЕ ТЕПЛА В БЕСКОНЕЧНОМ ТЕЛЕ
 2 августа, 2016
2 августа, 2016  Oleg Maloletnikov
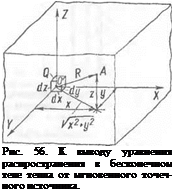
Oleg Maloletnikov Мгновенный точечный источник. Предположим, чго в очень малый объем массивного тела вблизи точки О (рис. 36) в течение короткого промежутка времени внесено некоторое количество тепла — Q, кал. Для упрощения расчетов будем считать тело
бесконечно большим, а источник тепла — неподвижным, точечным, мгновенным. В качестве граничных условий примем, что 1) теплообмена на границах тела нет, так как они удалены в бесконечность;
2)
в начальный момент времени температура постоянна по всему объему и равна нулю (Т0 = 0). Тогда решение уравнения теплопроводности для данных условий будет таким:
где T — температура исследуемой точки А тела с координатами х, у, 2, °С;
t — время от момента внесения тепла, сек є — основание натуральных логарифмов;
R — расстояние исследуемой точки А тела от точки О внесения тепла, см. Если считать, что начало координат находится в точке внесения тепла, то R — ]/х2 + У2 + г2.
 Выражение (IV. 19) является частным решением дифференциального уравнения теплопроводности (IV. 18). В правильности этого выражения можно убедиться, вычислив из него частные производные температуры и подставив их в уравнение (IV. 18). Последнее в этом случае обращается в тождество.
Выражение (IV. 19) является частным решением дифференциального уравнения теплопроводности (IV. 18). В правильности этого выражения можно убедиться, вычислив из него частные производные температуры и подставив их в уравнение (IV. 18). Последнее в этом случае обращается в тождество.
Выражение (IV. 19) представляет собой произведение двух множителей, из которых первый - —ГГ вы-
г су (4тмО /а
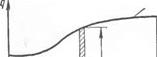
ражает температуру в точке гнесения тепла в разные моменты времени, а второй характеризует изменение температуры для различных точек тела в зависимости от R и /. В самом деле, для точки внесения тепла R — 0
![]() = 1; Т(0, t) =
= 1; Т(0, t) =
С увеличением Rat температура точек тела падает. В связи с тем что тепло равномерно распространяется от точки внесения во все стороны, изотермами для указанного случая будут правильные шаровые поверхности с центром в точке приложения тепла и радиусом R.
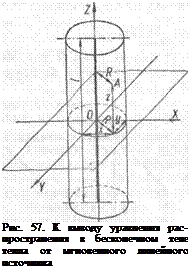
Мгновенный линейный источник. Предположим, что некоторое количество тепла Q внесено в неограниченное теплопроводящее тело и распределено по прямой, совпадающей с осью Z (рис. 57). Это означает, что мы принимаем такую расчетную схему: бесконечное тело, мгновенный линейный неподвижный источник. Граничные
условия выберем ге же, что и в предыдущем случае. Интенсивность источника, т. е. количество тепла, приходящееся на единицу
длины, примем равной <?,. Тогда Q, = j калієм, где I — длина
прямой, по которой распределено тепло.
В этом случае тепло распространяется равномерно во все стороны от источника тепла. Изотермическими поверхностями будут цилиндры с общей осью Z, т. е. температура не зависит от координаты z. Тогда решение дифференциального уравнения теплопроводности
 примет вид
примет вид
(‘V-20»
где R — расстояние от исследуемой точки А до источника теп - ла ;/?=]/у! остальные обозначения — те же, что и в предыдущей формуле. Мгновенный плоский источник. Если в тело неограниченных размеров тепло внесено мгновенно и распределено по некоторой плоскости равномерно, то распространение его будет происходить только в обе стороны от этой плоскости перпендикулярно к ней ц подчиняться единому закону.
Для этого случая справедливо дифференциальное уравнение (IV.186). Учтя граничные условия и приняв интенсивность источника тепла Q2 —f калісма, где Q — общее количество тепла, введенного источником, a F — площадь, на которой это тепло распределилось, можно решить уравнение (IV. 186), в результате чего получить выражение для Т (х, t):
(IV-2I>
В этом выражении х—расстояние от исследуемой точки до плоскости источника тепла. Так как температура точек тела не зависит от координат у и 2, то для любых точек тела с координатой х в данный момент времени она есть величина постоянная.
Изотермические поверхности будут представлять собой в этом случае плоскости, параллельные плоскости источника тепла.
Принцип наложения. Мы рассмотрели идеализированные мгновенные источники тепла простейших форм: точечный, линейный
ПО
и плоский. На самом деле нам придется иметь дело с источниками, непрерывно действующими более или менее продолжительное время и распространенными в большем или меньшем объеме.
 Для расчета процессов распространения тепла от реальных источников воспользуемся принципом наложения элементарных решений. Сущность его состоит в том, что температура от совместного действия совокупности распределенных в пространстве или времени источников принимается равной сумме температур от действия каждого отдельного источника. Допустимость принципа наложения, или принципа независимости действия источников, проверена опытом. Пользуясь этим принципом, можно представить реальный источник любой формы как совокупность сосредоточенных источников (точечных, линейных и плоских), а непрерывно действующий источник — как совокупность мгновенных источников, соответственно распределенных по времени действия источника. Просуммировав решения для каждого элементарного мгновенного источника, найдем решение для источника любой формы, действующего любое время. При пользовании принципом наложения коэффициенты теплофизических свойств материала Я, су, о. прини мают постоянными, не зависящими от температуры.
Для расчета процессов распространения тепла от реальных источников воспользуемся принципом наложения элементарных решений. Сущность его состоит в том, что температура от совместного действия совокупности распределенных в пространстве или времени источников принимается равной сумме температур от действия каждого отдельного источника. Допустимость принципа наложения, или принципа независимости действия источников, проверена опытом. Пользуясь этим принципом, можно представить реальный источник любой формы как совокупность сосредоточенных источников (точечных, линейных и плоских), а непрерывно действующий источник — как совокупность мгновенных источников, соответственно распределенных по времени действия источника. Просуммировав решения для каждого элементарного мгновенного источника, найдем решение для источника любой формы, действующего любое время. При пользовании принципом наложения коэффициенты теплофизических свойств материала Я, су, о. прини мают постоянными, не зависящими от температуры.
Распределенный по объему источник (выравнивание начального распределения температур). Применим принцип наложения для отыскания закона выравнивания начального распределения температуры.
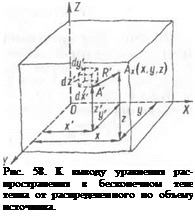
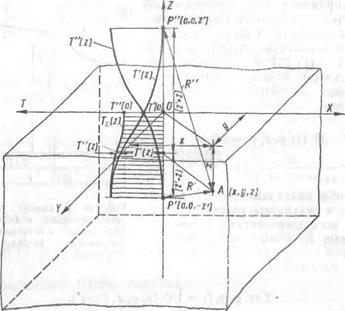
Пусть в некоторый момент времени t = 0, который мы примем за начало отсчета, в бесконечном теле распределение тепла описывается функцией Тп (лг, у, г). В произвольной точке А этого тела (рис. 58) выделим элементарный объем dx'dy'dz'. Температуру точки А' в начальный момент можно будет найти, если в выражение Т0 (х, У, z) для начальной температуры подставить координаты х', у, г точки.
Поскольку выделенный бесконечно малый объем имеет некоторое количество тепла dQ, то можно считать его мгновенным точечным источником. Количество тепла, заключенное в таком объеме, определим умножением этого объема на теплоемкость и температуру:
dQ = dx' dy' dz' cjT0 (x’, y', z’). (IV.22)
Эго тепло, независимо от наличия других тепловых источников, будет распространяться как от точечного мгновенного источника
 |
Здесь R' — расстояние от источника тепла (элементарного объема с координатами х', у', г'), выделенного вблизи точки А', до произвольной точки тела Ах с текущими координатами х, у, г. Как видно из рис. 58,
(R'f = (X - хТ + (у - у'? + (2 - z'f.
На точку Ах с координатами х, у, г действует не только выделенный элементарный источник, но, в соответствии с принципом наложения, и все другие элементарные объемы тела, рассматриваемые как отдельные источники тепла. Поэтому температура в точке Ак будет суммой всех температур, возникающих в ней в результате действия отдельных элементарных объемов:
Т (х, у, 2, I) = [ &Т (х, у, г, /). (IV.22a)
V
![]()
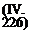
Но поскольку
то, учтя выражение (IV.22), получим
l г -151’
Т(х, у, 2, t) = (4—у, j Т0 (/, у', z') dx' dy' dz' е ш, (IV.23)
и
где интегрирование производится по всему объему тела.
Аналогичные рассуждения можно провести и для линейных и плоских мгновенных источников.
Непрерывно действующие сосредоточенные источники. Чтобы вывести зависимости распространения тепла при действии непрерывных сосредоточенных источников, воспользуемся известными выражениями для мгновенных источников тепла. Используя принцип наложения, представим процесс непрерывного введения тепла в нагреваемое тело как сумму мгновенных внесений бесконечно малых порций тепла dQ через очень малые промежутки времени dt.
Пусть в течение времени I непрерывно действует тепловой источник мощностью q (t) кал! сек (рис. 59). Разобьем все время действия источника t на бесконечно малые отрезки времени ctf, через которые в тело вносится мгновенная порция тепла. Тогда в некоторый произ-
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
Адиабатическая граница — такая граница, которая не пропускает тепло.
Пусть граничная плоскость XOY (рис. 60) полубесконечного тела непроницаема для тепла. На оси Z в точке Р' (0,0,— г') приложен мгновенный точечный источник тепла Q. Если бы вблизи источника не было границы, то тепло от него распространялось бы по уже известному закону (IV. 19), изображенному кривой Т (г).
Мысленно дополним имеющееся полубесконечное тело второй
|
Рис. СО. Схема распространения тепла в теле при наличии адиабатической границы. |
половиной и поместим в нее фиктивный тепловой источник таким образом, чтобы он создал во всех точках поверхности раздела те же температуры, что и основной. Тогда на границе не будет теплового обмена, так как здесь разность температур в любой точке основного и дополнительного тела равна нулю. Этот искусственный прием позволяет перейти от полубесконечного тела к бесконечному и в то же время выдержать заданное граничное условие.
Чтобы тепловые поля в основном и дополнительном теле были одинаковыми, фиктивный источник, очевидно, должен иметь одинаковую тепловую мощность с основным и находиться на таком же расстоянии от граничной плоскости — зеркачьно по отношению к основному. Тогда решение задачи сводится к определению температуры, возникающей в любой точке бесконечного тела в результате совместного действия двух ИСТОЧНИКОВ равной МОЩНОСТИ,
Ж
расположенных в точках Р' (0,0,—г') и Р" (0,0,г'). По принципу наложения их общее воздействие равно сумме воздействий каждого:
7 (г) = Г (2) + Т" (г).
Расстояние от основного источника тепла Р' до исследуемой точки тела А (х, у, z)
R' = Ух* + У* + (z'-2)2,
а от вспомогательного источника Р" до той же точки R” = V*2+ У2 + (г' + zf.
Температура исследуемой точки А от совместного действия обоих источников
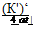
![]()
![]()
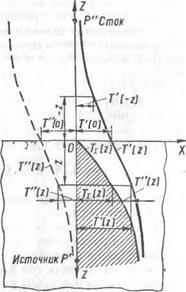
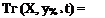 су (4тса/)3/г
су (4тса/)3/г
![]() о
о
![]() ст (4r. at У
ст (4r. at У
Физически этот случай можно представить следующим образом: тепловой поток, дойдя до не пропускающей тепло границы, отражается от нее и распространяется в обратном направлении по тому же закону, по которому он распространялся* бы дальше в бесконечном теле, если бы не было адиабатической границы. Температуры точек тела вблизи адиабатической границы равны сумме температур, возникших в этих точках в результате действия основного и отраженного тепловых потоков.
Изотермическая граница — такая граница, которая имеет постоянную температуру независимо от теплового состояния тела.
Нужно исследовать распределение температур в полубесконеч - ном теле, температура поверхности которого постоянна (рис. 61). С помощью рассуждений, аналогичных предыдущему, установим, что после дополнения полубесконечного тела второй половиной мы должны воспользоваться таким фиктивным источником тепла, который на границе даст температуры, равные по величине и обратные по знаку тем, которые получились бы в бесконечном теле. Такие фиктивные «отрицательные» источники тепла называют стоками тепла. Тогда сумма температур любой точки поверхности основного
и вспомогательного тел будет равна нулю, что и требовалось По условию.
Сток тепла, равный по мощности источнику, следует одновременно с источником приложить в точке Р", являющейся зеркальным отображением точки Р' относительно граничной плоскости XOY. Тогда по принципу наложения температура в любой точке тела с текущими координатами х, у, г будет равна разности температур двух процессов — нагрева тела и стока тепла:
Мы познакомились с основными положениями теории тепловых процессов сварки. Покажем, как используются эти положения при решении конкретных вопросов (см. далее). Все примеры взяты для дуговой сварки как наиболее важного и изученного технологического процесса и относятся к простым типовым случаям. Здесь не приведены расчеты тепловых процессов при газовой сварке, контактной электросварке и пр., так как они содержатся в соответствующих курсах и специальных работах.
Расчеты нагрева метал л а сварочной д у - г о й. Полную тепловую мощность дуги определяют умножением ее электрической мощности на коэффициент перехода от электрических единиц к тепловым, равный 0,239 или — 0,24.
Для постоянного тока тепловая мощность дуги
<7 - 0,24 W = 0,24 1U = 0,24 PR кал',сек,
где W — электрическая мощность дуги, вт;
/ — ток дуги, а;
V — напряжение дуги, в;
R — сопротивление дуги, ом.
Поскольку не все тепло, выделенное в дуге, расходуется на нагрев изделия, а часть его идет на нагревание атмосферы и окружающих предметов путем конвекции и радиации, то эффективная тепловая мощность дуги qu всегда меньше полной тепловой мощности q. Отношение их характеризует степень использования терла дуги на нагрев изделия, f
Эффективный коэффициент процесса нагрева изделия дугой
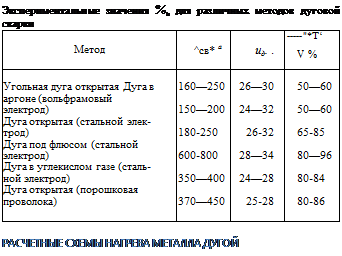
зависит от технологии сварки, длины дуги, степени углубления ее в металл и пр. Опытные значения ria для различных методов сварки приведены в табл. 11.
Эффективный к. п. д. снижается при увеличении длины дуги и растет по мере углубления дуги в металл.
Точность тепловых расчетов в значительной мере зависит от правильности выбора идеализированной расчетной схемы.
 Сварочная дуга представляет собой концентрированный в малом объеме источник тепла, поэтому во многих случаях расчета можно считать ее точечным или линейным источником.
Сварочная дуга представляет собой концентрированный в малом объеме источник тепла, поэтому во многих случаях расчета можно считать ее точечным или линейным источником.
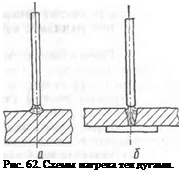
Нагрев тел дугами поверхностного типа (рис. 62, а) ближе к схеме «точечный источник на поверхности полубесконечного тела». Погруженные дуги (рис. 62, б), применяемые при стыковой сварке листов с полным проплавлением за один проход, дают тепловые поля, хорошо совпадающие с тепловыми полями, рассчитанными по схеме линейного источника.
При исследовании распространения тепла и определении температур в непосредственной близости от дуги последняя не может считаться точечным источником, так как ее размеры одного порядка с расстоянием между исследуемой точкой и источником тепла.
Для расчета температур при наплавке на пластину могут быть использованы такие расчетные комбинации: «точечный источник — плоский слой» либо «линейный источник — пластина». Первая схема дает более точные результаты для областей, в которых температура заметно меняется по толщине, тогда как на значительном расстоянии от валика, где температуру можно принимать
практически постоянной по толшине пластины, применима вторая расчетная комбинация.
Сварочная дуга, вообще говоря,— всегда непрерывно действующий источник. Однако если горение ее продолжалось недолго, как это бывает при прихватке или сварке электрозаклепками (а нас интересует температура тела через промежутки времени, во много раз превышающие период горения), то можно считать источник тепла мгновенным. Такое допущение мало отразится на точности расчета.
В зависимости от скорости перемещения сварочная дуга может быть неподвижным, подвижным и быстродвижущимся источником тепла. Схему подвижного источника часто применяют для расчета температур при ручной дуговой сварке, тогда как схема быстродви - жущегося источника больше удовлетворяет условиям автоматической сварки. При этом чем выше скорость сварки и меньше расстояние от исследуемой точки до шва, тем точнее будет совпадать теоретическая схема с практическими результатами.
Вообще при выборе расчетных схем следует учитывать принцип местного влияния, который утверждает, что температурное поле существенно зависит от размеров и характера распределения источника тепла только на расстояниях одного порядка сего размерами, тогда как на больших расстояниях температурное поле практически не зависит от формы источника и занимаемого им объема.

 Опубликовано в
Опубликовано в